群体智能算法之粒子群算法

1. 简介

自然界中的一些生物行为特征呈现出群体的特征，这种群体的特征在计算机中建模，实际上就是在计算中用一些简单的规则来定义群体运动的行为方式。虽然每个个体的行为方式可能很简单，但是组成群体过程中的行为特征就复杂了很多。一般情况下，群体智能应当遵循的5条基本原则如下：
(1) 临近原则：群体能够进行简单的空间计算和时间计算。
(2) 品质原则：群体能够响应环境中的品质因子。
(3) 多样性反应原则：群体的行动范围不应该太窄。
(4) 稳定性原则：群体不应当在每次环境变化的时候都改变自身的行为。
(5) 适应性原则：在所需代价不太高的情况下，群体能够在适当的时候改变自身的行为。
上述的原则说明实现群体智能的智能主体必须能够在环境中表现出自主性、反应性、学习性和自适应性等智能特性，而群体智能的核心在于由众多的简单个体行为通过相互之间的合作实现较为复杂的功能，完成某一项任务。
有一种称为boid模型，这个模型有三种行为：分离、列队以及聚集，并能够感知周围一定范围内其他boid飞行信息。boid根据该信息，结合其自身当前的飞行状态，并在三条简单行为规则的指导下做出下一步的飞行决策：
(1) 冲突避免。群体在一定空间移动，个体有自己的移动意志，但不能够影响其他个体移动，避免碰撞与争执。
(2) 速度匹配。个体必须配合中心移动速度，不管在方向、距离与速率上必须配合。
(3) 群体中心聚集。个体会飞向群体的中心区域，向邻近个体的平均位置移动。
鸟群中的每只鸟在初始状态下是处于随机位置向各个随机方向飞行的，但是随着时间的推移，这些初始处于随机状态的鸟通过自组织的形式逐步聚集成一个个小的群落，并且以相同的速度朝着相同的方向飞行。在模拟之前，需要对群鸟的位置和飞翔的速度赋值初始值，鸟飞行的原则会根据自己以及群体的历史信息选择新的飞行速度和飞行方向。群鸟在觅食过程中，每只鸟在初始时候并不知道食物在哪里，但是随着时间的推移，这些处于初始状态随机位置的鸟类通过群体相互学习、信息共享和个体不断积累寻觅食物的经验，自发地形成一个个群落，朝着目标飞行。局部最优是指每只鸟能够记住自己所找到的最好位置，全局最优是指群鸟中所有个体中找到的最好的位置。这就是粒子群算法(PSO)基本模型。

2. 粒子群算法(PSO)算法数学模型

2.1 数学模型

设$X_i=(x_{i1},x_{i2},...,x_{in})$是微粒$i$的当前位置，$V_i=(v_{i1},v_{i2},...,v_{in})$为微粒$i$当前飞行速度，$P_i=(p_{i1},p_{i2},...,p_{in})$是微粒$i$所经历的最好位置，即微粒$i$所经历过的具有最好适应值的位置称为个体的最好位置。设目标函数$f(X)$是最小化的目标函数，那么微粒$i$当前最好的位置由下面的公式确定：
$$P_i(t+1)=\{\begin{array}{ll}{P}_i(t)& ,f(X_i(t+1))\ge f(P_i(t))\\ X_i(t+1)& ,f(X_i(t+1))<f(P_i(t))\end{array}$$

设群体中的微粒数为$s$，群体中所有微粒经过最好的位置为$P_g(t)$，$P_g(t)\in \{P_0(t),P_1(t),...,P_s(t)\}$,
$$f(P_g(t))=\min \{f(P_0(t)),f(P_1(t)),...,f(P_s(t))\}$$

粒子群算法的进化方程可以描述为
$$v_{ij}(t+1)=w{v}_{ij}(t)+c_1{r}_{1j}(t)(p_{ij}(t)-x_{ij}(t))+c_2{r}_{2j}(t)(p_{gj}(t)-x_{ij}(t))$$

$$x_{ij}(t+1)=x_{ij}(t)+v_{ij}(t+1)$$

式子中$w$为惯性权重。粒子群算法是惯性权重$w=1$的特殊情况；下标$j$表示粒子的第$j$维度；$i$表示微粒$i$；$t$代表第$t$代；$c_1,c_2$表示加速常数，通常$c_1,c_2\in [0,2]$；$r_1\sim U(0,1),r_2\sim U(0,1)$为两个相互独立的随机函数，一般取均匀分布。
粒子进化方程可以看出，$c_1$调节微粒飞向自身最好位置方向的步长，$c_2$调节微粒向全局最好的位置飞行的步长。为了减少在进化过程中微粒离开搜索空间的可能性，$v_{ij}$一般情况下限定于一定 范围内，即$v_{ij}\in [-v_{max},v_{max}]$。特别地，问题空间限定在$[-x_{max},x_{max}]$的时候，可以选择设定$v_{max}=k{x}_{max},k\in [0.1,1.0]$。

2.2 算法流程

基本粒子群算法的具体实现步骤如下所示：
步骤一：参数初始化。粒子群算法的初始化过程包括设定种群规模$N$；对于任意$i,j$，在$[-x_{max},x_{max}]$内服从均匀分布产生$x_{ij}$；对于任意$i,j$，在$[-v_{max},v_{max}]$内服从均匀分布产生$v_{ij}$；对于任意$i$，设$P_i=X_i$。
步骤二：计算每个粒子的适应值。
步骤三：对于每一个微粒，将其适应值与所经历过的最好位置$P_i$的适应值进行比较，若比较好，则将其作为当前的最好位置。
步骤四：对于每一个微粒，将其适应值与全局所经历的最好位置$P_g$的适应值进行比较，若较好，则将其作为当前的全局最好位置。
步骤五：更新每一个微粒的位置信息和速度信息。
步骤六：如果未满足条件。

3. 具体应用

我们依旧使用TSP问题来应用这一个模型。TSP问题的描述可以看笔者博文群体智能算法之模拟退火算法。数据集选取TSP数据集中的eil51.tsp作为本节的测试数据集。
对于TSP问题，首先引入几个定义和概念性问题：
交换子和交换序
设$n$个数字的某一个全排列序列为$S=(a_1,a_2,...,a_i,...,a_n)$。定义交换子$SO(i_1,i_2)$是序列$S$中点$a_{i_1}$和$a_{i_2}$进行交换操作，则
$$S{}^{\prime }=S+S_o(i_1,i_2)$$

表示序列$S$经过算子$SO(i_1,i_2)$操作之后的新解。
一个或者多个交换子的有序队列被称作是交换序，记做$SS$，其中
$$SS=(S{O}_1,S{O}_2,...,S{O}_n)$$

$SS$中的有序交换子的顺序是有意义的，意味着所有的交换子依次作用于某个解上。
符号与定义
若干个交换序可以合并为一个新的交换序，定义$\oplus$为两个交换序的合并算子。设两个交换序$SS1$和$SS2$按照先后顺序作用于解$S$上，于是得到了新的解$S{}^{\prime }$。假设另外有一个交换序作用于同一个解$S$上，能够得到形同的解$S{}^{\prime }$，则定义合并有序算子：
$$SS{}^{\prime }=S{S}_1\oplus S{S}_2$$

显然这种$\oplus$运算是不遵循交换律的，即
$$S{S}_1\oplus S{S}_2\ne S{S}_2\oplus S{S}_1$$

这是由于交换算子的有序性导致这种运算的性质的。$SS{}^{\prime }$和$S{S}_1\oplus S{S}_2$属于同一个等价集，在交换序等价集中，拥有最少交换子的交换序被称为该等价集的基本交换序。

所以在求解TSP问题中速度和位置的更新表达式如下所示：
$$\{\begin{array}{l}{v}_{id}=v_{id}\oplus (p_{id}-x_{id})\oplus (p_{gd}-x_{id})\\ x_{id}=x_{id}+v_{id}\end{array}$$

这就是标准的TSPPSO算法。在标准算法基础进行一些改进的方法。我们设常数$\omega ,\alpha ,\beta$为交换序变异率,$c_1,c_2,c_3$为$[0,1]$内均匀分布的随机数，另外设函数：
$$v_{new}=f_{rate}(v_{pre},rate)=\{\begin{array}{ll}{v}_{pre}& ,\text{ if }{c}_1>rate\\ \eta (v_{pre})& ,\text{ if }{c}_2<rate\end{array}$$

$\eta$表示交换序变异函数，代表交换算子之间的交换、交换序列的子序列部分交换或者是交换序列中交换子缺失、增加(也就是交换子的变异过程，类似于遗传算法)。

那么我们改进版本的PSO算法如下所示：

$$\{\begin{array}{l}{v}_{id}=v_{id}\oplus f_{\omega }(f_{\alpha }(p_{id}-x_{id})\oplus f_{\beta }(p_{gd}-x_{id}))\\ x_{id}=x_{id}+v_{id}\end{array}$$

实验的结果如下所示：

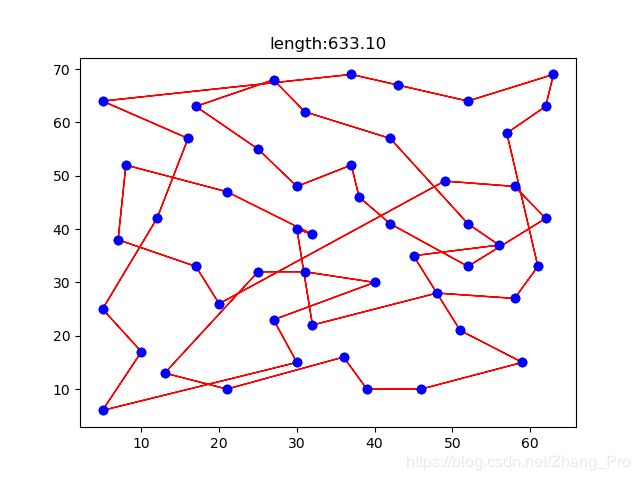
路径长度变化图如下所示：

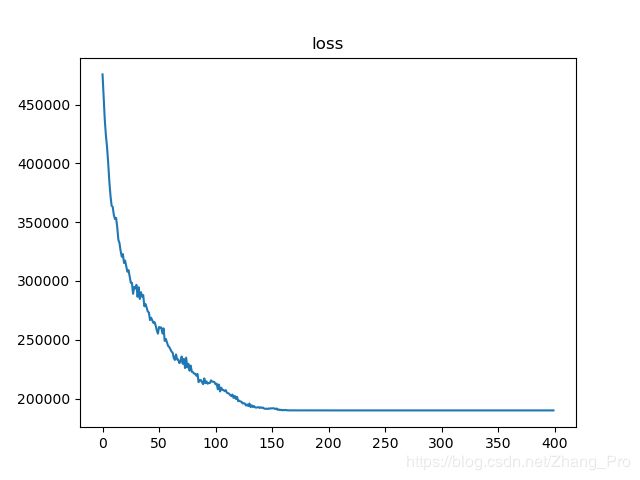
从整体上来说，算法是是收敛的，不足之处就是不能够很好地在有限空间内进行搜索最优解，这是不足之处。具体代码可以参考笔者github

4. PSO算法的参数选取原则

在上述式子中，参数$c_1$是控制种群中粒子在自己的维度上与最好位置的的距离，参数$c_2$是控制粒子在种群总维度上的最好距离，这两个参数需要合适地选择，以便更好地收敛。$c_1$参数太大，则种群随机搜索性能大大提高，但是种群的收敛性能降低；太小的话，可以加速种群的收敛速度，但是随机搜索性能降低。所以这个参数主要是为搜索局部变量。$c_2$是能够将全局收敛到最优值的一个参数，对于收敛性有着重要的影响。

5. 改进版本的PSO算法

由于标准的PSO算法中在收敛性上、求解值搜索空间上等方面有些欠缺，所以在很多方面对PSO算法有很多改进，例如基于遗传算法改进版本的PSO算法、基于退火算法改进版本的PSO算法。我们就PSO本身系统的改进阐述PSO算法的改进版本。

5.1 捕食逃逸粒子群算法

5.1.1 算法基本原理和描述

捕食逃逸粒子群算法是受到捕食者逃逸现象启发而提出的一种改进的粒子群算法，在这种算法中，微粒进一步将分为两类群体：捕食微粒群体(PS)和逃逸微粒群体(ES)。PS粒子和ES粒子的行为将依据各自定义的简单规则将以约束，其中，PS粒子追捕ES的gBest粒子，故而对于ES粒子造成不等的捕食风险，所以gBest粒子也能够从PS粒子获取信息，实现了群体的对称社会认知。当ES粒子与PS粒子的距离接近逃逸开始距离(FID)的时候产生逃逸，逃逸的速度依赖于自身的能量状态(适应度)，能量越大逃逸能力越强；如果ES粒子与PS粒子的距离小于FID的时候，则ES粒子进行确定性变异，变异前后的ES例子优胜劣汰。随着迭代次数逐步增加，将逐步降低PS粒子对ES粒子的影响，从而增加群体的局部搜索能力，从而实现算法的全局收敛性。
在这种改进版本中算法中，有以下的几个定义：

• 捕食风险： 也称作是捕食压力，是指在一定时间内ES粒子被捕食的概率，即$P_i^{ES}=exp(-{\alpha }_{i}kt{}^{\prime })$；其中，${\alpha }_i$表示ES粒子$i$与PS粒子相遇的概率，它取决于它们之间的距离和当前PS粒子的密度信息，即${\alpha }_i=exp(-\frac{\text{distance}}{n_1}\times \beta )$，$\beta$为控制参数，$n_1$是PS微粒的规模，distance为ES粒子$i$与最近PS之间的距离；$k$表示PS粒子攻击ES粒子的概率(固定值为1)；$t{}^{\prime }=\frac{t+T}{T}$，$t$为当前的迭代数，$T$为最大的迭代数，迭代时间会逐步降低捕食粒子对被捕食粒子的影响。
• 能量状态： 指的是ES粒子当前的饥饿状态，表现为该粒子的适应度与ES平均适应度的比值，即
  $$E_i^{ES}(t)=\frac{f_i^{ES}(t)}{f_{avg}^{ES}(t)}$$
• 警觉距离： 反映出了ES粒子对PS粒子的警惕能力，是一种普遍的社群现象，其大小随着群体的密度和群体规模增加而减小，即有
  $$D^{ES}=\text{FID}\times (1+\frac{n_1}{\rho \times n_2})$$

式子中，$\rho$表示当前群体局部密度；$n_1,n_2$分别表示PS粒子和ES粒子的规模。

5.1.2 算法流程

步骤一：随机产生并初始化$n_1$个PS粒子和$n_2$个ES粒子，$m=n_1+n_2$；设置$t=0,\text{FID}$控制参数。
步骤二：计算每个粒子的适应度。
步骤三：对每个粒子$i$，将其适应度值与其历史最好位置${\text{pBest}}_i$进行比较，更新${\text{pBest}}_i$和$\text{gBest}$。
步骤四：对于每个PS粒子$i$，按照以下的公式更新其速度和位置信息：
$$V_{ij}^{PS}(t+1)=w{V}_{ij}^{PS}(t)+c_1{r}_{1j}(p_{ij}^{PS}(t)-X_{ij}^{PS}(t))+c_2{r}_{2j}(p_{gj}^{PS}(t)-X_{ij}^{PS}(t))$$

$$X_{ij}^{PS}(t+1)=X_{ij}^{PS}(t)+V_{ij}^{PS}(t+1)$$

步骤五：对于每个ES粒子$i$，
(1) 若${\text{distance}}_j\ge \text{FID}$，按照以下的公式更新其速度和位置：
$$\begin{gathered} V_{ij}^{ES}(t+1)=w{V}_{ij}^{ES}(t)+c_1{r}_{1j}(p_{ij}^{ES}(t)-X_{id}^{ES}(t))+c_2{r}_{2j}(p_{gj}^{ES}(t)-X_{id}^{ES}(t)) \\ +c_3{r}_{3j}\text{sign}(D^{ES}-{\text{distance}}_j)E_i^{ES}(t)X_{max}(1-P_i^{ES}(t)) \end{gathered}$$

$$X_{ij}^{ES}(t+1)=X_{ij}^{ES}(t)+V_{ij}^{ES}(t+1)$$
式子当中，${\text{distance}}_j$表示ES粒子$i$与第$d$维度最近PS粒子之间的距离；$\text{sign}$表示$0-1$阀值函数；$X_{max}$表示位置的最大取值；$c_3$为捕食影响因子；$r_3$为$[0,1]$内均匀分布的随机数。
(2) 若 ${\text{distance}}_j<\text{FID}$，则粒子$i$捕食，即对其位置进行变异，变异前后的例子优胜劣汰，但维持变异之前粒子的速度$V_i^{ES}(t)$和${\text{pBest}}_i$。
步骤六：判断满足终止条件。若未满足，则$t=t+1$转步骤二。

5.2 权重值的调节

在求解问题过程中，固定值的$w$如若是定值，则限制了粒子的飞行空间和速度，不能够很好地适应函数，所以这样就提出了一些动态调整权重值$w$的方法，如下所示

• 随机调整： 每一次迭代过程中都随机选取一个$w$，其中一种方法可以是通过随机分布函数生成带有范围值的$w$。例如从高斯分布中选取值：
  $$w\sim N(0.72,{\sigma }^2)$$

其中，$\sigma$是一个足够小的值确保$w$不会显著的大于$1$。还有一种取值方式是通过线性取值$r_1$和$r_2$的值：
$$w=c_1{r}_1+c_1{r}_2$$

• 线性递减： $w$从较大的取值(0.9)线性递减至一个较小的值(0.4)。可以使用下面的公式进行递减：
  $$w(t)=(w(0)-w(n_t))\cdot \frac{n_t-t}{n_t}+w(n_t)$$
  其中，$n_t$是算法执行的最大迭代次数，$w(0)$是初始的惯性权重值，$w(n_t)$是最终的惯性权重值，$w(t)$是$t$时刻的惯性权重值。但是要满足$w(0)>w(n_t)$。
• 非线性递减： $w$从开始比较大的取值非线性递减至一个较小的值。非线性递减方法可以使得允许一个较短时间的探索工作，可以用于比较光滑的搜索空间中使用。以下有几种方法进行递减操作：
  方法一：
  $$w(t+1)=\frac{(w(t)-0.4)(n_t-t)}{n_t+0.4}$$
  其中$w(0)=0.9$。
  方法二：
  $$w(t+1)=\alpha w(t{}^{\prime })$$
  其中，$\alpha =0.975$，$t^{{}^{\prime }}$是惯性上一次改变的时间步。

6. 小结

本小结讲述了PSO算法的原理、应用以及改进的方法，应当注意到的是，学会将不同的问题用于PSO算法的解决。笔者会在后面的博文中进一步使用PSO算法使用到其他问题当中。

参考文献

[1] https://wenku.baidu.com/view/58939d14f18583d0496459ac.html
[2] 仿生智能计算，科学出版社
[3] 计算群体智能基础，清华大学出版社
[4] MATLAB在数学建模中的应用，卓金武