新手入门第一课——什么是深度学习？百度AI Studio

新手入门第一课——什么是深度学习？

大家好，欢迎来到新手入门课程，在这里我会带领大家从一个完全不懂深度学习的小白，通过学习本课程后，能够了解基本的深度学习概念，熟悉必备的数序基础知识，学会常见的编程工具Python，并掌握实用的深度学习框架PaddlePaddle。可能看到本课程的你并不了解什么是深度学习，那么就让我们从第一课开始把——什么是深度学习？

一、深度学习的发展历程

1.1 Turing Testing (图灵测试)

图灵测试是人工智能是否真正能够成功的一个标准，“计算机科学之父”、“人工智能之父”英国数学家图灵在1950年的论文《机器会思考吗》中提出了图灵测试的概念。即把一个人和一台计算机分别放在两个隔离的房间中，房间外的一个人同时询问人和计算机相同的问题，如果房间外的人无法分别哪个是人，哪个是计算机，就能够说明计算机具有人工智能。

1.2 医学上的发现

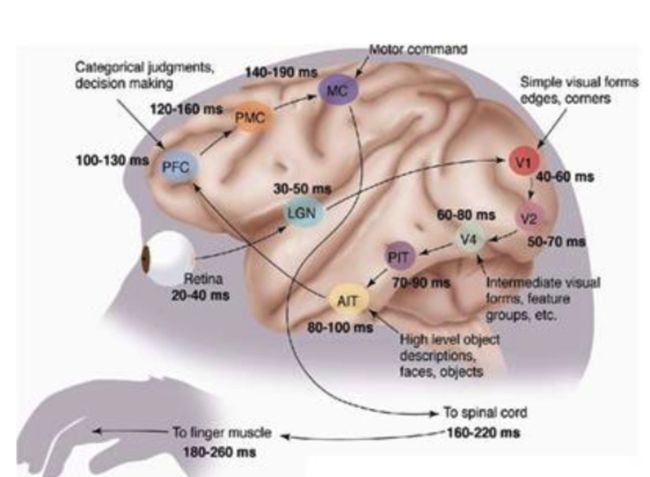
1981年的诺贝尔将颁发给了David Hubel和Torsten Wiesel，以及Roger Sperry。他们发现了人的视觉系统处理信息是分级的。

从视网膜（Retina）出发，经过低级的V1区提取边缘特征，到V2区的基本形状或目标的局部，再到高层的整个目标（如判定为一张人脸），以及到更高层的PFC（前额叶皮层）进行分类判断等。也就是说高层的特征是低层特征的组合，从低层到高层的特征表达越来越抽象和概念化，也即越来越能表现语义或者意图。

边缘特征 —–> 基本形状和目标的局部特征——>整个目标 这个过程其实和我们的常识是相吻合的，因为复杂的图形，往往就是由一些基本结构组合而成的。同时我们还可以看出：大脑是一个深度架构，认知过程也是深度的。

人脑神经元示意图

计算机识别图像的过程

1.3 Deep Learning的出现

低层次特征 - - - - (组合) - - ->抽象的高层特征

深度学习，恰恰就是通过组合低层特征形成更加抽象的高层特征（或属性类别）。例如，在计算机视觉领域，深度学习算法从原始图像去学习得到一个低层次表达，例如边缘检测器、小波滤波器等，然后在这些低层次表达的基础上，通过线性或者非线性组合，来获得一个高层次的表达。此外，不仅图像存在这个规律，声音也是类似的。比如，研究人员从某个声音库中通过算法自动发现了20种基本的声音结构，其余的声音都可以由这20种基本结构来合成！

二、机器学习

机器学习是实现人工智能的一种手段，也是目前被认为比较有效的实现人工智能的手段，目前在业界使用机器学习比较突出的领域很多，例如：计算机视觉、自然语言处理、推荐系统等等。大家生活中经常用到的比如高速上的ETC的车牌识别，今日头条的新闻推荐，天猫上的评价描述。 机器学习是人工智能的一个分支，而在很多时候，几乎成为人工智能的代名词。简单来说，机器学习就是通过算法，使得机器能从大量历史数据中学习规律，从而对新的样本做智能识别或对未来做预测。

2.1 人工智能vs机器学习

人工智能是计算机科学的一个分支，研究计算机中智能行为的仿真。

每当一台机器根据一组预先定义的解决问题的规则来完成任务时，这种行为就被称为人工智能。

开发人员引入了大量计算机需要遵守的规则。计算机内部存在一个可能行为的具体清单，它会根据这个清单做出决定。如今，人工智能是一个概括性术语，涵盖了从高级算法到实际机器人的所有内容。

我们有四个不同层次的AI，让我们来解释前两个:

• 弱人工智能，也被称为狭义人工智能，是一种为特定的任务而设计和训练的人工智能系统。弱人工智能的形式之一是虚拟个人助理，比如苹果公司的Siri。
• 强人工智能，又称人工通用智能，是一种具有人类普遍认知能力的人工智能系统。当计算机遇到不熟悉的任务时，它具有足够的智能去寻找解决方案。

机器学习是指计算机使用大数据集而不是硬编码规则来学习的能力。

机器学习允许计算机自己学习。这种学习方式利用了现代计算机的处理能力，可以轻松地处理大型数据集。

基本上，机器学习是人工智能的一个子集;更为具体地说，它只是一种实现AI的技术，一种训练算法的模型，这种算法使得计算机能够学习如何做出决策。

从某种意义上来说，机器学习程序根据计算机所接触的数据来进行自我调整。

2.2 监督式学习vs非监督式学习

监督式学习需要使用有输入和预期输出标记的数据集。

当你使用监督式学习训练人工智能时，你需要提供一个输入并告诉它预期的输出结果。

如果人工智能产生的输出结果是错误的，它将重新调整自己的计算。这个过程将在数据集上不断迭代地完成，直到AI不再出错。

监督式学习的一个例子是天气预报人工智能。它学会利用历史数据来预测天气。训练数据包含输入(过去天气的压力、湿度、风速)和输出(过去天气的温度)。

我们还可以想象您正在提供一个带有标记数据的计算机程序。例如，如果指定的任务是使用一种图像分类算法对男孩和女孩的图像进行分类，那么男孩的图像需要带有“男孩”标签，女孩的图像需要带有“女孩”标签。这些数据被认为是一个“训练”数据集，直到程序能够以可接受的速率成功地对图像进行分类，以上的标签才会失去作用。

它之所以被称为监督式学习，是因为算法从训练数据集学习的过程就像是一位老师正在监督学习。在我们预先知道正确的分类答案的情况下，算法对训练数据不断进行迭代预测，然后预测结果由“老师”进行不断修正。当算法达到可接受的性能水平时，学习过程才会停止。

非监督式学习是利用既不分类也不标记的信息进行机器学习，并允许算法在没有指导的情况下对这些信息进行操作。

当你使用非监督式学习训练人工智能时，你可以让人工智能对数据进行逻辑分类。这里机器的任务是根据相似性、模式和差异性对未排序的信息进行分组，而不需要事先对数据进行处理。

非监督式学习的一个例子是亚马逊等电子商务网站的行为预测AI。

它将创建自己输入数据的分类，帮助亚马逊识别哪种用户最有可能购买不同的产品(交叉销售策略)。 另一个例子是，程序可以任意地使用以下两种算法中的一种来完成男孩女孩的图像分类任务。一种算法被称为“聚类”，它根据诸如头发长度、下巴大小、眼睛位置等特征将相似的对象分到同一个组。另一种算法被称为“相关”，它根据自己发现的相似性创建if/then规则。换句话说，它确定了图像之间的公共模式，并相应地对它们进行分类。

三、深度学习如何工作

什么是深度学习，以及它是如何工作的。

深度学习是一种机器学习方法 ， 它允许我们训练人工智能来预测输出，给定一组输入(指传入或传出计算机的信息)。监督学习和非监督学习都可以用来训练人工智能。

Andrew Ng：“与深度学习类似的是，火箭发动机是深度学习模型，燃料是我们可以提供给这些算法的海量数据。”

我们将通过建立一个公交票价估算在线服务来了解深度学习是如何工作的。为了训练它，我们将使用监督学习方法。

我们希望我们的巴士票价估价师使用以下信息/输入来预测价格: 

3.1 神经网络

神经网络是一组粗略模仿人类大脑，用于模式识别的算法。神经网络这个术语来源于这些系统架构设计背后的灵感，这些系统是用于模拟生物大脑自身神经网络的基本结构，以便计算机能够执行特定的任务。

和人类一样， “AI价格评估”也是由神经元(圆圈)组成的。此外，这些神经元还是相互连接的。

神经元分为三种不同类型的层次：

• 输入层接收输入数据。在我们的例子中，输入层有四个神经元:出发站、目的地站、出发日期和巴士公司。输入层会将输入数据传递给第一个隐藏层。

• 隐藏层对输入数据进行数学计算。创建神经网络的挑战之一是决定隐藏层的数量，以及每一层中的神经元的数量。

• 人工神经网络的输出层是神经元的最后一层，主要作用是为此程序产生给定的输出，在本例中输出结果是预测的价格值。

神经元之间的每个连接都有一个权重。这个权重表示输入值的重要性。模型所做的就是学习每个元素对价格的贡献有多少。这些“贡献”是模型中的权重。一个特征的权重越高，说明该特征比其他特征更为重要。

在预测公交票价时，出发日期是影响最终票价的最为重要的因素之一。因此，出发日期的神经元连接具有较大的“权重”。

每个神经元都有一个激活函数。它主要是一个根据输入传递输出的函数。 当一组输入数据通过神经网络中的所有层时，最终通过输出层返回输出数据。

3.2 通过训练改进神经网络

为了提高“AI价格评估”的精度，我们需要将其预测结果与过去的结果进行比较，为此，我们需要两个要素:

• 大量的计算能力；
• 大量的数据。

训练AI的过程中，重要的是给它的输入数据集(一个数据集是一个单独地或组合地或作为一个整体被访问的数据集合),此外还需要对其输出结果与数据集中的输出结果进行对比。因为AI一直是“新的”，它的输出结果有可能是错误的。

对于我们的公交票价模型，我们必须找到过去票价的历史数据。由于有大量“公交车站”和“出发日期”的可能组合，因而我们需要一个非常大的票价清单。

一旦我们遍历了整个数据集，就有可能创建一个函数来衡量AI输出与实际输出(历史数据)之间的差异。这个函数叫做成本函数。即成本函数是一个衡量模型准确率的指标，衡量依据为此模型估计X与Y间关系的能力。

模型训练的目标是使成本函数等于零，即当AI的输出结果与数据集的输出结果一致时（成本函数等于0）。

3.3 我们如何降低成本函数呢?

通过使用一种叫做梯度下降的方法。梯度衡量得是，如果你稍微改变一下输入值，函数的输出值会发生多大的变化。

梯度下降法是一种求函数最小值的方法。在这种情况下，目标是取得成本函数的最小值。 它通过每次数据集迭代之后优化模型的权重来训练模型。通过计算某一权重集下代价函数的梯度，可以看出最小值的梯度方向。

为了降低成本函数值，多次遍历数据集非常重要。这就是为什么需要大量计算能力的原因。 一旦我们通过训练改进了AI，我们就可以利用它根据上述四个要素来预测未来的价格。

四、看看第一个例子吧！

4.1 初识神经网络

我们来看一个具体的神经网络示例，使用 PaddlePaddle来学习手写数字分类。如果你没用过PaddlePaddle或类似的库，可能无法立刻搞懂这个例子中的全部内容。甚至你可能还没有安装PaddlePaddle, 没关系，第四课会教大家如何安装PaddlePaddle，学会基本的命令和操作。因此，如果其中某些步骤看起来不太明白也不要担心。下面我们要开始了。

我们这里要解决的问题是，将手写数字的灰度图像（28 像素×28 像素）划分到 10 个类别 中（0~9）。我们将使用 MNIST 数据集，它是机器学习领域的一个经典数据集，其历史几乎和这 个领域一样长，而且已被人们深入研究。这个数据集包含 60 000 张训练图像和 10 000 张测试图 像，由美国国家标准与技术研究院（National Institute of Standards and Technology，即 MNIST 中 的 NIST）在 20 世纪 80 年代收集得到。你可以将“解决”MNIST 问题看作深度学习的“Hello World”，正是用它来验证你的算法是否按预期运行。当你成为机器学习从业者后，会发现 MNIST 一次又一次地出现在科学论文、博客文章等中。

Step1:准备数据

MINIST数据集包含60000个训练集和10000测试数据集。分为图片和标签，图片是28*28的像素矩阵，标签为0~9共10个数字。 2.定义读取MNIST数据集的train_reader和test_reader，指定一个Batch的大小为128，也就是一次训练或验证128张图像。 3.paddle.dataset.mnist.train()或test()接口已经为我们对图片进行了灰度处理、归一化、居中处理等处理。

In[7]

#导入需要的包
import numpy as np
import paddle as paddle
import paddle.fluid as fluid
from PIL import Image
import matplotlib.pyplot as plt
import os

train_reader = paddle.batch(paddle.reader.shuffle(paddle.dataset.mnist.train(),
                                                  buf_size=512),
                    batch_size=128)
test_reader = paddle.batch(paddle.dataset.mnist.test(),
                           batch_size=128)

打印一下，观察一下mnist数据集

In[8]

temp_reader = paddle.batch(paddle.dataset.mnist.train(),
                           batch_size=1)
temp_data=next(temp_reader())
print(temp_data)

[(array([-1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -0.9764706 , -0.85882354, -0.85882354,
       -0.85882354, -0.01176471,  0.06666672,  0.37254906, -0.79607844,
        0.30196083,  1.        ,  0.9372549 , -0.00392157, -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -0.7647059 , -0.7176471 , -0.26274508,  0.20784318,
        0.33333337,  0.9843137 ,  0.9843137 ,  0.9843137 ,  0.9843137 ,
        0.9843137 ,  0.7647059 ,  0.34901965,  0.9843137 ,  0.8980392 ,
        0.5294118 , -0.4980392 , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -0.6156863 ,  0.8666667 ,
        0.9843137 ,  0.9843137 ,  0.9843137 ,  0.9843137 ,  0.9843137 ,
        0.9843137 ,  0.9843137 ,  0.9843137 ,  0.96862745, -0.27058822,
       -0.35686272, -0.35686272, -0.56078434, -0.69411767, -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -0.85882354,  0.7176471 ,  0.9843137 ,  0.9843137 ,
        0.9843137 ,  0.9843137 ,  0.9843137 ,  0.5529412 ,  0.427451  ,
        0.9372549 ,  0.8901961 , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -0.372549  ,  0.22352946, -0.1607843 ,  0.9843137 ,  0.9843137 ,
        0.60784316, -0.9137255 , -1.        , -0.6627451 ,  0.20784318,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -0.8901961 ,
       -0.99215686,  0.20784318,  0.9843137 , -0.29411763, -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        ,  0.09019613,
        0.9843137 ,  0.4901961 , -0.9843137 , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -0.9137255 ,  0.4901961 ,  0.9843137 ,
       -0.45098037, -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -0.7254902 ,  0.8901961 ,  0.7647059 ,  0.254902  ,
       -0.15294117, -0.99215686, -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -0.36470586,  0.88235295,  0.9843137 ,  0.9843137 , -0.06666666,
       -0.8039216 , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -0.64705884,
        0.45882356,  0.9843137 ,  0.9843137 ,  0.17647064, -0.7882353 ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -0.8745098 , -0.27058822,
        0.9764706 ,  0.9843137 ,  0.4666667 , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        ,  0.9529412 ,  0.9843137 ,
        0.9529412 , -0.4980392 , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -0.6392157 ,  0.0196079 ,
        0.43529415,  0.9843137 ,  0.9843137 ,  0.62352943, -0.9843137 ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -0.69411767,
        0.16078436,  0.79607844,  0.9843137 ,  0.9843137 ,  0.9843137 ,
        0.9607843 ,  0.427451  , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -0.8117647 , -0.10588235,  0.73333335,  0.9843137 ,  0.9843137 ,
        0.9843137 ,  0.9843137 ,  0.5764706 , -0.38823527, -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -0.81960785, -0.4823529 ,  0.67058825,  0.9843137 ,
        0.9843137 ,  0.9843137 ,  0.9843137 ,  0.5529412 , -0.36470586,
       -0.9843137 , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -0.85882354,  0.3411765 ,  0.7176471 ,
        0.9843137 ,  0.9843137 ,  0.9843137 ,  0.9843137 ,  0.5294118 ,
       -0.372549  , -0.92941177, -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -0.5686275 ,  0.34901965,
        0.77254903,  0.9843137 ,  0.9843137 ,  0.9843137 ,  0.9843137 ,
        0.9137255 ,  0.04313731, -0.9137255 , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        ,  0.06666672,  0.9843137 ,  0.9843137 ,  0.9843137 ,
        0.6627451 ,  0.05882359,  0.03529418, -0.8745098 , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        , -1.        ,
       -1.        , -1.        , -1.        , -1.        ], dtype=float32), 5)]

Step2:配置网络

以下的代码判断就是定义一个简单的多层感知器，一共有三层，两个大小为100的隐层和一个大小为10的输出层，因为MNIST数据集是手写0到9的灰度图像，类别有10个，所以最后的输出大小是10。最后输出层的激活函数是Softmax，所以最后的输出层相当于一个分类器。加上一个输入层的话，多层感知器的结构是：输入层-->>隐层-->>隐层-->>输出层。

In[9]

# 定义多层感知器
def multilayer_perceptron(input):
    # 第一个全连接层，激活函数为ReLU
    hidden1 = fluid.layers.fc(input=input, size=100, act='relu')
    # 第二个全连接层，激活函数为ReLU
    hidden2 = fluid.layers.fc(input=hidden1, size=100, act='relu')
    # 以softmax为激活函数的全连接输出层，大小为10
    prediction = fluid.layers.fc(input=hidden2, size=10, act='softmax')
    return prediction

定义输入层，输入的是图像数据。图像是2828的灰度图，所以输入的形状是[1, 28, 28]，如果图像是3232的彩色图，那么输入的形状是[3. 32, 32]，因为灰度图只有一个通道，而彩色图有RGB三个通道。

In[10]

# 定义输入输出层
image = fluid.layers.data(name='image', shape=[1, 28, 28], dtype='float32')  #单通道，28*28像素值
label = fluid.layers.data(name='label', shape=[1], dtype='int64')            #图片标签

在这里调用定义好的网络来获取分类器

In[11]

# 获取分类器
model = multilayer_perceptron(image)

接着是定义损失函数，这次使用的是交叉熵损失函数，该函数在分类任务上比较常用。定义了一个损失函数之后，还有对它求平均值，因为定义的是一个Batch的损失值。同时我们还可以定义一个准确率函数，这个可以在我们训练的时候输出分类的准确率。

In[12]

# 获取损失函数和准确率函数
cost = fluid.layers.cross_entropy(input=model, label=label)  #使用交叉熵损失函数,描述真实样本标签和预测概率之间的差值
avg_cost = fluid.layers.mean(cost)
acc = fluid.layers.accuracy(input=model, label=label)

接着是定义优化方法，这次我们使用的是Adam优化方法，同时指定学习率为0.001。

In[13]

# 定义优化方法
optimizer = fluid.optimizer.AdamOptimizer(learning_rate=0.001)   #使用Adam算法进行优化
opts = optimizer.minimize(avg_cost)

Step3:模型训练 & STEP4:模型评估

接着也是定义一个解析器和初始化参数

In[14]

# 定义一个使用CPU的解析器
place = fluid.CPUPlace()
exe = fluid.Executor(place)
# 进行参数初始化
exe.run(fluid.default_startup_program())

[]

输入的数据维度是图像数据和图像对应的标签，每个类别的图像都要对应一个标签，这个标签是从0递增的整型数值。

In[15]

# 定义输入数据维度
feeder = fluid.DataFeeder(place=place, feed_list=[image, label])

最后就可以开始训练了，我们这次训练5个Pass。在上面我们已经定义了一个求准确率的函数，所以我们在训练的时候让它输出当前的准确率，计算准确率的原理很简单，就是把训练是预测的结果和真实的值比较，求出准确率。每一个Pass训练结束之后，再进行一次测试，使用测试集进行测试，并求出当前的Cost和准确率的平均值。

In[16]

# 开始训练和测试
for pass_id in range(5):
    # 进行训练
    for batch_id, data in enumerate(train_reader()):                        #遍历train_reader
        train_cost, train_acc = exe.run(program=fluid.default_main_program(),#运行主程序
                                        feed=feeder.feed(data),             #给模型喂入数据
                                        fetch_list=[avg_cost, acc])         #fetch 误差、准确率
        # 每100个batch打印一次信息  误差、准确率
        if batch_id % 100 == 0:
            print('Pass:%d, Batch:%d, Cost:%0.5f, Accuracy:%0.5f' %
                  (pass_id, batch_id, train_cost[0], train_acc[0]))

    # 进行测试
    test_accs = []
    test_costs = []
    #每训练一轮 进行一次测试
    for batch_id, data in enumerate(test_reader()):                         #遍历test_reader
        test_cost, test_acc = exe.run(program=fluid.default_main_program(), #执行训练程序
                                      feed=feeder.feed(data),               #喂入数据
                                      fetch_list=[avg_cost, acc])           #fetch 误差、准确率
        test_accs.append(test_acc[0])                                       #每个batch的准确率
        test_costs.append(test_cost[0])                                     #每个batch的误差
    # 求测试结果的平均值
    test_cost = (sum(test_costs) / len(test_costs))                         #每轮的平均误差
    test_acc = (sum(test_accs) / len(test_accs))                            #每轮的平均准确率
    print('Test:%d, Cost:%0.5f, Accuracy:%0.5f' % (pass_id, test_cost, test_acc))
    
    #保存模型
    model_save_dir = "/home/aistudio/data/hand.inference.model"
    # 如果保存路径不存在就创建
    if not os.path.exists(model_save_dir):
        os.makedirs(model_save_dir)
    print ('save models to %s' % (model_save_dir))
    fluid.io.save_inference_model(model_save_dir,  #保存推理model的路径
                                  ['image'],      #推理（inference）需要 feed 的数据
                                  [model],        #保存推理（inference）结果的 Variables
                                  exe)            #executor 保存 inference model

Pass:0, Batch:0, Cost:2.45102, Accuracy:0.07812
Pass:0, Batch:100, Cost:0.40899, Accuracy:0.85156
Pass:0, Batch:200, Cost:0.29173, Accuracy:0.92969
Pass:0, Batch:300, Cost:0.24797, Accuracy:0.91406
Pass:0, Batch:400, Cost:0.16732, Accuracy:0.95312
Test:0, Cost:0.21080, Accuracy:0.93720
save models to /home/aistudio/data/hand.inference.model
Pass:1, Batch:0, Cost:0.15709, Accuracy:0.95312
Pass:1, Batch:100, Cost:0.22466, Accuracy:0.93750
Pass:1, Batch:200, Cost:0.23914, Accuracy:0.92969
Pass:1, Batch:300, Cost:0.13536, Accuracy:0.96094
Pass:1, Batch:400, Cost:0.25973, Accuracy:0.92188
Test:1, Cost:0.13641, Accuracy:0.95758
save models to /home/aistudio/data/hand.inference.model
Pass:2, Batch:0, Cost:0.11116, Accuracy:0.97656
Pass:2, Batch:100, Cost:0.11151, Accuracy:0.93750
Pass:2, Batch:200, Cost:0.17952, Accuracy:0.95312
Pass:2, Batch:300, Cost:0.09100, Accuracy:0.97656
Pass:2, Batch:400, Cost:0.20766, Accuracy:0.94531
Test:2, Cost:0.10600, Accuracy:0.96687
save models to /home/aistudio/data/hand.inference.model
Pass:3, Batch:0, Cost:0.12874, Accuracy:0.96094
Pass:3, Batch:100, Cost:0.07218, Accuracy:0.98438
Pass:3, Batch:200, Cost:0.05249, Accuracy:0.99219
Pass:3, Batch:300, Cost:0.06613, Accuracy:0.98438
Pass:3, Batch:400, Cost:0.11549, Accuracy:0.95312
Test:3, Cost:0.09244, Accuracy:0.97102
save models to /home/aistudio/data/hand.inference.model
Pass:4, Batch:0, Cost:0.15327, Accuracy:0.95312
Pass:4, Batch:100, Cost:0.13707, Accuracy:0.92188
Pass:4, Batch:200, Cost:0.05426, Accuracy:0.97656
Pass:4, Batch:300, Cost:0.05081, Accuracy:0.99219
Pass:4, Batch:400, Cost:0.09514, Accuracy:0.96875
Test:4, Cost:0.07361, Accuracy:0.97617
save models to /home/aistudio/data/hand.inference.model

Step5:模型预测

在预测之前，要对图像进行预处理，处理方式要跟训练的时候一样。首先进行灰度化，然后压缩图像大小为28*28，接着将图像转换成一维向量，最后再对一维向量进行归一化处理。

In[23]

# 对图片进行预处理
def load_image(file):
    im = Image.open(file).convert('L')                        #将RGB转化为灰度图像，L代表灰度图像，灰度图像的像素值在0~255之间
    im = im.resize((28, 28), Image.ANTIALIAS)                 #resize image with high-quality 图像大小为28*28
    im = np.array(im).reshape(1, 1, 28, 28).astype(np.float32)#返回新形状的数组,把它变成一个 numpy 数组以匹配数据馈送格式。
   # print(im)
    im = im / 255.0 * 2.0 - 1.0                               #归一化到【-1~1】之间
    print(im)
    return im

img = Image.open('data/6.png')
plt.imshow(img)   #根据数组绘制图像
plt.show()        #显示图像

In[27]

infer_exe = fluid.Executor(place)
inference_scope = fluid.core.Scope()

最后把图像转换成一维向量并进行预测，数据从feed中的image传入。fetch_list的值是网络模型的最后一层分类器，所以输出的结果是10个标签的概率值，这些概率值的总和为1。

In[28]

# 加载数据并开始预测
with fluid.scope_guard(inference_scope):
    #获取训练好的模型
    #从指定目录中加载 推理model(inference model)
    [inference_program,                                           #推理Program
     feed_target_names,                                           #是一个str列表，它包含需要在推理 Program 中提供数据的变量的名称。 
     fetch_targets] = fluid.io.load_inference_model(model_save_dir,#fetch_targets：是一个 Variable 列表，从中我们可以得到推断结果。model_save_dir：模型保存的路径
                                                    infer_exe)     #infer_exe: 运行 inference model的 executor
    img = load_image('data/6.png')

    results = exe.run(program=inference_program,     #运行推测程序
                   feed={feed_target_names[0]: img}, #喂入要预测的img
                   fetch_list=fetch_targets)         #得到推测结果,    

[[[[-0.9843137  -0.9843137  -0.9843137  -0.9843137  -0.9843137
    -0.9843137  -0.9843137  -0.9843137  -0.9843137  -0.9843137
    -0.9843137  -0.9843137  -0.9843137  -0.9843137  -0.9843137
    -0.9843137  -0.9764706  -0.9372549  -0.9372549  -0.96862745
    -0.9843137  -1.         -1.         -1.         -0.9607843
    -0.9843137  -0.9843137  -0.9843137 ]
   [-0.9843137  -0.9843137  -0.9843137  -0.9843137  -0.9843137
    -0.9843137  -0.9843137  -0.9843137  -0.9843137  -0.9843137
    -0.9843137  -0.9843137  -0.9843137  -0.9843137  -0.9843137
    -0.9843137  -0.99215686 -0.9529412  -0.92156863 -0.9607843
    -0.99215686 -0.81960785 -0.41960782 -0.654902   -0.9529412
    -0.9843137  -0.9843137  -0.9843137 ]
   [-0.9843137  -0.9843137  -0.9843137  -0.9843137  -0.9843137
    -0.9843137  -0.9843137  -0.9843137  -0.9843137  -0.9843137
    -0.9843137  -0.9843137  -0.9843137  -0.9843137  -0.9843137
    -0.9843137  -0.99215686 -1.         -0.9764706  -0.92156863
    -0.9529412  -0.29411763  0.827451    0.14509809 -0.9607843
    -0.9843137  -0.9843137  -0.9843137 ]
   [-0.9843137  -0.9843137  -0.9843137  -0.9843137  -0.9843137
    -0.9843137  -0.9843137  -0.9843137  -0.9843137  -0.9843137
    -0.9843137  -0.9843137  -0.9843137  -0.9843137  -0.9843137
    -0.99215686 -0.9372549  -0.90588236 -0.99215686 -1.
    -0.7647059   0.34901965  0.7176471  -0.30196077 -0.92941177
    -0.9843137  -0.9843137  -0.9843137 ]
   [-0.9843137  -0.9843137  -0.9843137  -0.9843137  -0.9843137
    -0.9843137  -0.9843137  -0.9843137  -0.9843137  -0.9843137
    -0.9843137  -0.9843137  -0.9843137  -0.9843137  -0.9843137
    -0.99215686 -0.92156863 -0.8352941  -0.8745098  -0.7254902
     0.01176476  0.6392157  -0.1372549  -0.9843137  -0.9607843
    -0.9843137  -0.9843137  -0.9843137 ]
   [-0.9843137  -0.9843137  -0.9843137  -0.9843137  -0.9843137
    -0.9843137  -0.9843137  -0.9843137  -0.9843137  -0.9843137
    -0.9843137  -0.9843137  -0.9843137  -0.9843137  -0.9843137
    -0.99215686 -0.9607843  -0.9764706  -0.77254903  0.09803927
     0.9372549   0.12941182 -0.96862745 -0.8901961  -0.96862745
    -0.9843137  -0.9843137  -0.9843137 ]
   [-0.9843137  -0.9843137  -0.9843137  -0.9843137  -0.9843137
    -0.9843137  -0.9843137  -0.9843137  -0.9843137  -0.9843137
    -0.9843137  -0.9843137  -0.9843137  -0.9843137  -0.9843137
    -0.9764706  -0.9137255  -0.85882354 -0.15294117  0.654902
     0.27843142 -0.5921569  -0.9529412  -0.9529412  -1.
    -0.9843137  -0.9843137  -0.9843137 ]
   [-0.9843137  -0.9843137  -0.9843137  -0.9843137  -0.9843137
    -0.9843137  -0.9843137  -0.9843137  -0.9843137  -0.99215686
    -0.9843137  -0.99215686 -0.9843137  -0.9764706  -0.96862745
    -1.         -1.         -0.2235294   0.7882353   0.35686278
    -0.77254903 -1.         -0.90588236 -1.         -0.9764706
    -0.9843137  -0.9843137  -0.9843137 ]
   [-0.9843137  -0.9843137  -0.9843137  -0.9843137  -0.9843137
    -0.9843137  -0.9843137  -0.9843137  -0.9843137  -0.99215686
    -0.9843137  -0.9764706  -0.99215686 -0.9843137  -0.92156863
    -0.8745098  -0.5058824   0.54509807  0.49803925 -0.56078434
    -1.         -0.9607843  -0.96862745 -0.9843137  -0.9529412
    -0.9843137  -0.9843137  -0.9843137 ]
   [-0.9843137  -0.9843137  -0.9843137  -0.9843137  -0.9843137
    -0.9843137  -0.9843137  -0.9843137  -1.         -0.9764706
    -0.9764706  -0.94509804 -0.92941177 -0.94509804 -0.7647059
    -0.18431371  0.56078434  0.4431373  -0.3960784  -0.8666667
    -0.96862745 -0.96862745 -0.9843137  -0.9529412  -0.99215686
    -0.9843137  -0.9843137  -0.9843137 ]
   [-0.9843137  -0.9843137  -0.9843137  -0.9843137  -0.9843137
    -0.9843137  -0.9843137  -0.9843137  -0.9843137  -0.9764706
    -0.96862745 -0.9764706  -0.9137255  -0.6784314  -0.1372549
     0.6156863   0.6156863  -0.41176468 -0.8745098  -0.8509804
    -0.92156863 -0.9529412  -0.9529412  -0.8980392  -1.
    -0.9843137  -0.9843137  -0.9843137 ]
   [-0.9843137  -0.9843137  -0.9843137  -0.9843137  -0.9843137
    -0.9843137  -0.9843137  -0.9764706  -0.92941177 -0.9764706
    -0.88235295 -0.9529412  -0.92156863 -0.10588235  0.7411765
     0.5529412  -0.38039213 -1.         -0.9137255  -0.827451
    -0.94509804 -0.9764706  -0.9843137  -0.94509804 -0.9764706
    -0.9843137  -0.9843137  -0.9843137 ]
   [-0.9843137  -0.9843137  -0.9843137  -0.9843137  -0.9843137
    -0.9843137  -0.9843137  -0.9843137  -0.9843137  -0.92941177
    -0.9843137  -0.8745098  -0.14509803  0.5921569   0.45882356
    -0.41176468 -0.85882354 -0.84313726 -0.9529412  -0.99215686
    -0.92941177 -0.9137255  -1.         -0.9843137  -0.92941177
    -0.9843137  -0.9843137  -0.9843137 ]
   [-0.9843137  -0.9843137  -0.9843137  -0.9843137  -0.9843137
    -0.9843137  -0.9843137  -0.9843137  -0.9372549  -0.99215686
    -0.8980392   0.04313731  0.9529412   0.3176471  -0.6156863
    -0.27843136  0.30980396  0.06666672 -0.32549018 -0.7490196
    -0.9137255  -0.92156863 -0.96862745 -0.9372549  -1.
    -0.9843137  -0.9843137  -0.9843137 ]
   [-0.9843137  -0.9843137  -0.9843137  -0.9843137  -0.9843137
    -0.9843137  -0.9843137  -0.9843137  -0.9843137  -0.90588236
    -0.19215685  0.7019608   0.92156863  0.6         0.5372549
     0.75686276  0.8117647   0.827451    0.7882353  -0.01960784
    -0.9843137  -0.9764706  -0.90588236 -0.8745098  -1.
    -0.9843137  -0.9843137  -0.9843137 ]
   [-0.9843137  -0.9843137  -0.9843137  -0.9843137  -0.9764706
    -0.9764706  -0.9764706  -0.9764706  -0.8901961  -0.05098039
     0.79607844  1.          0.8509804   0.8901961   0.78039217
     0.12941182 -0.31764704  0.37254906  1.          0.3411765
    -0.9843137  -0.92156863 -0.8666667  -0.9607843  -0.99215686
    -0.9843137  -0.9843137  -0.9843137 ]
   [-0.9764706  -0.99215686 -0.96862745 -0.9529412  -0.8980392
    -0.8509804  -0.8745098  -0.90588236 -0.3098039   0.69411767
     0.9529412   0.8117647   0.27058828 -0.27843136 -0.6313726
    -0.8352941  -0.8901961   0.1686275   0.81960785 -0.05098039
    -0.77254903 -0.8352941  -0.96862745 -0.9529412  -0.9372549
    -0.9843137  -0.9843137  -0.9843137 ]
   [-0.9372549  -0.9372549  -0.96862745 -0.99215686 -0.9843137
    -0.94509804 -0.9764706  -0.7882353   0.52156866  0.9529412
     0.6627451  -0.31764704 -0.8666667  -0.9764706  -0.92156863
    -0.9764706  -0.41960782  0.6627451   0.34901965 -0.58431375
    -0.9764706  -0.9607843  -0.96862745 -0.92156863 -0.9764706
    -0.9843137  -0.9843137  -0.9843137 ]
   [-0.9843137  -0.96862745 -0.96862745 -0.96862745 -0.9607843
    -0.88235295 -0.7882353   0.02745104  0.6862745   0.28627455
    -0.36470586 -0.84313726 -0.9137255  -0.90588236 -0.96862745
    -0.38039213  0.52156866  0.4901961  -0.30196077 -0.90588236
    -1.         -0.99215686 -0.92941177 -0.90588236 -1.
    -0.9843137  -0.9843137  -0.9843137 ]
   [-0.9843137  -1.         -0.9607843  -0.8901961  -0.96862745
    -0.9764706  -0.7254902   0.69411767  0.9529412  -0.58431375
    -0.9843137  -0.84313726 -0.96862745 -0.6392157   0.20784318
     0.79607844  0.5294118  -0.30196077 -0.79607844 -0.9607843
    -0.92156863 -0.9764706  -0.9843137  -0.96862745 -0.99215686
    -0.9843137  -0.9843137  -0.9843137 ]
   [-0.9529412  -1.         -0.96862745 -0.8901961  -0.9843137
    -1.         -0.827451    0.60784316  0.99215686  0.5686275
     0.54509807  0.5372549   0.36470592  0.60784316  0.8901961
     0.62352943 -0.17647058 -0.8745098  -0.9529412  -0.92156863
    -0.9372549  -0.99215686 -1.         -0.9843137  -0.9372549
    -0.9843137  -0.9843137  -0.9843137 ]
   [-0.9764706  -0.99215686 -0.99215686 -0.96862745 -0.9529412
    -0.9137255  -0.8901961  -0.02745098  0.654902    1.
     1.          1.          0.5529412   0.1686275  -0.3098039
    -0.7647059  -0.9372549  -1.         -0.9764706  -0.96862745
    -0.9843137  -0.94509804 -0.9372549  -0.9843137  -0.9372549
    -0.9843137  -0.9843137  -0.9843137 ]
   [-0.9764706  -0.96862745 -0.9843137  -1.         -0.9843137
    -0.92941177 -0.96862745 -0.79607844 -0.67058825 -0.64705884
    -0.6627451  -0.6156863  -0.654902   -0.84313726 -0.84313726
    -0.92156863 -1.         -0.99215686 -0.99215686 -1.
    -0.9764706  -0.88235295 -0.88235295 -0.9372549  -0.9764706
    -0.9843137  -0.9843137  -0.9843137 ]
   [-0.9843137  -0.9764706  -0.9529412  -0.9843137  -0.99215686
    -0.9607843  -0.96862745 -1.         -1.         -0.99215686
    -1.         -1.         -0.81960785 -0.8509804  -0.92941177
    -0.9529412  -0.9764706  -0.9843137  -0.99215686 -0.9843137
    -0.94509804 -0.9607843  -0.9529412  -0.9137255  -0.9764706
    -0.9843137  -0.9843137  -0.9843137 ]
   [-0.9843137  -0.9843137  -0.96862745 -0.9843137  -0.9843137
    -0.9764706  -0.9764706  -0.9843137  -0.9764706  -0.94509804
    -0.9529412  -0.94509804 -0.8980392  -0.90588236 -0.9843137
    -1.         -0.99215686 -0.99215686 -0.99215686 -0.9843137
    -0.9764706  -1.         -0.99215686 -0.96862745 -0.9843137
    -0.99215686 -0.99215686 -0.99215686]
   [-0.9843137  -0.9843137  -0.9843137  -0.9843137  -0.9843137
    -0.9843137  -0.9843137  -0.9843137  -1.         -1.
    -1.         -0.9764706  -0.99215686 -1.         -0.99215686
    -1.         -1.         -0.99215686 -0.99215686 -0.99215686
    -0.99215686 -0.99215686 -0.99215686 -1.         -0.99215686
    -0.99215686 -0.99215686 -0.99215686]
   [-0.9843137  -0.9843137  -0.9843137  -0.9843137  -0.9843137
    -0.9843137  -0.9843137  -0.9843137  -1.         -1.
    -0.99215686 -0.9764706  -0.9764706  -0.9843137  -0.99215686
    -1.         -1.         -0.99215686 -0.99215686 -0.99215686
    -0.99215686 -0.99215686 -0.99215686 -0.99215686 -0.99215686
    -0.99215686 -0.99215686 -0.99215686]
   [-0.9843137  -0.9843137  -0.9843137  -0.9843137  -0.9843137
    -0.9843137  -0.9843137  -0.9843137  -1.         -0.99215686
    -0.99215686 -0.9843137  -0.9843137  -0.99215686 -0.99215686
    -1.         -1.         -0.99215686 -0.99215686 -0.99215686
    -0.99215686 -0.99215686 -0.99215686 -0.99215686 -0.99215686
    -0.99215686 -0.99215686 -0.99215686]]]]

拿到每个标签的概率值之后，我们要获取概率最大的标签，并打印出来。

In[29]

# 获取概率最大的label
lab = np.argsort(results)                               #argsort函数返回的是result数组值从小到大的索引值
#print(lab)
print("该图片的预测结果的label为: %d" % lab[0][0][-1])  #-1代表读取数组中倒数第一列  

该图片的预测结果的label为: 6

五、总结

到这里是不是觉得深度学习非常神奇呢？它具体是怎么实现的呢？背后有什么数学原理？在了解数学原理之前，先学习一下深度学习中常见的数学知识，第二节课就会带领大家学习必备的数学知识~