图--最小生成树之解
**
Graph:
**
(应用:地图,社交关系等)
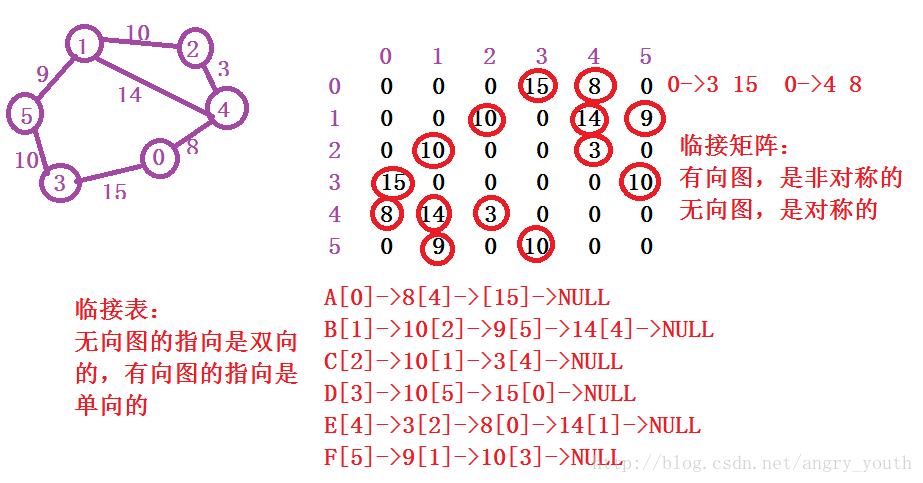
图是一种非线性结构,由顶点集合以及顶点间的关系集合组成的一种数据结构;
1) 完全图:如果一个N个顶点组成的无向图中有N*(N-1)/2条边,则为无向完全图(即任意两个顶点间都有边相连)
2) 权重:边具有与之相关的数值,则称为权重;
3) 临接顶点:if(u,v)是图中的一条边,则u和v互为临接顶点;
4) 度:与顶点相关联的边的数目称为顶点的度;
5) 连通图和强连通图:在无向图中v1到v2有路径,则称为v1,v2是连通的,如果任意两个顶点都是连通的,那么就是连通图;
强连通图:在有向图中,若每一对顶点之间都存在路径,那么就是强连通图
6) 生成树:一个无向连通图的生成树是它的极小连通图,若途中有N个顶点,则生成树也由N-1条边构成;
//临接矩阵
template <class V,class W,bool IsDirected = true>
class GraphMartix
{
protected:
vector* _next;
GraphListEdge(const int& src,const int& dst,const W& w)
:_src(src),_dst(dst),_w(w),_next(NULL)
{}
};
template <class V,class W,bool IsDirected = true>
class GraphList
{
typedef GraphListEdge List;
typedef GraphList Self;
protected:
vector **深度优先和广度优先:
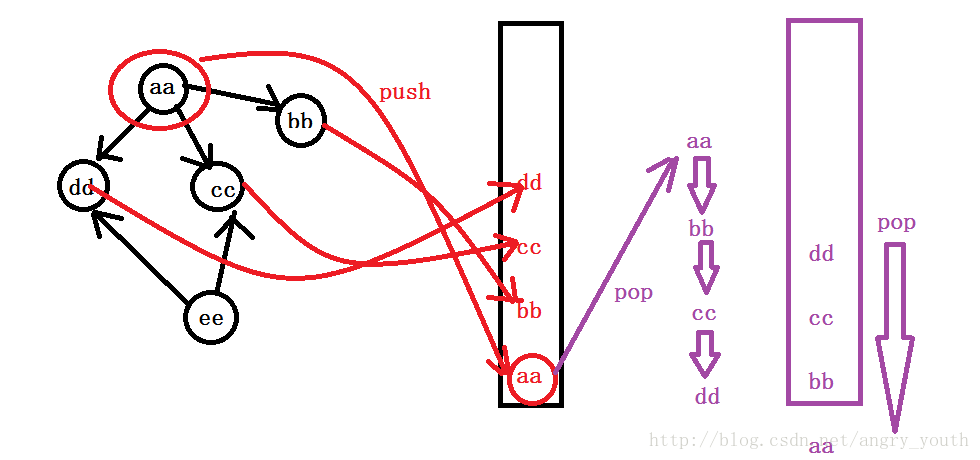
深度优先:标记走过的点——–>递归**
类似于迷宫问题:每次访问一个新的结点,将其标记,然后判断与这个新节点相连接的谁没有访问,如果有没有访问的结点就会进入访问,如果没有就会回退到上一个结点继续进行判断谁还没有访问,再这样一直循环,一直回退到起始结点,访问结束;
//深度优先----利用递归的方式
void DFS(const V& src)
{
size_t srcIndex = GetIndex(src);
vector<bool> visited;
visited.resize(_vertex.size(),false);
_DFS(srcIndex,visited);
cout<void _DFS(size_t src,vector<bool>& visited)
{
cout<<_vertex[src]<<"["<"]"<<"->";
visited[src] = true;
List* list = _LinkEdge[src];
while(list)
{
if(visited[list->_dst] == false)
{
_DFS(list->_dst,visited);
}
list = list->_next;
}
} 广度优先:利用queue,先进先出,做标记
思想:将与某个结点有关联的所有结点都push进如队列中,然后在一个一个pop取出访问,做标记
//广度优先----利用队列的方式
void BFS(const V& src)
{
size_t srcIndex = GetIndex(src);
vector<bool> visited;
visited.resize(_vertex.size(),false);
queue<int> q;
q.push(srcIndex);
while(!q.empty())
{
size_t src = q.front();
q.pop();
if(visited[src] == false)
{
visited[src] = true;
cout<<_vertex[src]<<"["<"]"<<"->";
List* list = _LinkEdge[src];
while(list)
{
if(visited[list->_dst] == false)
{
q.push(list->_dst);
}
list = list->_next;
}
}
}
cout< 找出最小生成树的方法:
Kruskal:
设计思想:把所有边根据权值大小建一个小堆,然后每次取出权值最小的边(top并pop),然后利用并查集判断边的两端顶点是否在同一个集合,如果是就舍弃该边,如果不是就添加这条边到最小生成树里面,再重新取出最小权值的边(top并pop),然后继续重复以上步骤,直到队列为空,或者已经找到最小生成树后退出;
判断两个节点是否相连———并查集(判断是否构成环)
每次都要找出一条最短的路径———-优先级队列(建小堆)

//克鲁斯卡尔算法
bool Kruskal(Self& minTree)
{
minTree._vertex = _vertex;
minTree._LinkEdge.resize(_vertex.size(),NULL);
minTree._indexMap = _indexMap;
struct EdgeCompare
{
bool operator()(const List* src,const List* dst)
{
return src->_w > dst->_w;
}
};
priority_queuevector,EdgeCompare> pq;
for(size_t i = 0; i < _LinkEdge.size(); i++)
{
List* list = _LinkEdge[i];
while(list)
{
if(IsDirected == false)
{
if(list->_src > list->_dst)
{
pq.push(list);//建小堆
}
}
else
pq.push(list);
list = list->_next;
}
}
UnionFindSet ufs(_vertex.size());
size_t N = _vertex.size() - 1;//最小生成树的结点个数是N-1个
while(!pq.empty())
{
List* list = pq.top();
pq.pop();
if(ufs.IsOneUnion(list->_src,list->_dst) == false)
{
minTree._AddEdge(list->_src,list->_dst,list->_w);
if(IsDirected == false)
{
minTree._AddEdge(list->_dst,list->_src,list->_w);
}
ufs.SetUnion(list->_src,list->_dst);
if(--N == 0)
{
return true;
}
}
}
return false;
}