Python数据挖掘—回归—一元非线性回归

1、使用scatter_matrix判断个特征的数据分布及其关系

散步矩阵(scatter_matrix)

Pandas中散步矩阵的函数原理

1 def scatter_matrix(frame, alpha=0.5, figsize=None, ax=None, diagonal='hist', marker='.', density_kwds=None,hist_kwds=None, range_padding=0.05, **kwds)

参数如下：

• frame:(DataFrame)，DataFrame对象
• alpha:(float,可选)，图像透明度，一般取(0,1]
• figsize:((float,float),可选)，以英寸单位的图像大小，一般以元组(width,height)形式设置
• ax:(Matplotlib axis object,可选)，一般取None
• diagonal:({"hist","kde"})，必须只能从这两个中选一个，"hist"表示直方图(Histogram plot)，“kde”表示核密度估计(Kernel Density Estimation);该参数是scatter_matrix函数的关键参数
• marker：（str，可选），Matplotlib可用的标记类型，如：‘，’，‘.’，‘o’
• density_kwds：（other plotting keyword argumentss，可选），与kde相关的字典参数
• hist_kwds：(other plotting keyword arguments，可选)，与hist相关的字典参数
• range_padding：（float，可选），图像在x轴，y轴原点附近的留白(padding)，该值越大，留白距离越大，图像远离坐标原点
• kwds:(other plotting keyword argumentss，可选)与scatter_matrix函数本身相关的字典参数

kde值

diagonal参数取’kde’值时，表示散布矩阵的对角线上的图形为数据集各特征的核密度估计(Kernel Density Estimation，KDE)。核密度估计是在概率论中用来估计未知的密度函数，属于非参数检验方法之一。简单来说，核密度估计就是在当前数据集(连续型数据样本)已知的情况下，通过计算来获取该样本分布的概率密度函数；在计算获取时需要用到核函数，如Gaussian Kernel Density、Exponential Kernel Density、Cosine Kernel Density等，不同核函数可以得到样本整体趋势和密度分布规律性基本一致的结果；影响该结果的还包括带宽（bandwidth），带宽值过大或过小都会影响估计结果；

---- 来自 Felix_YU_Q 的CSDN 博客 ，全文地址请点击：https://blog.csdn.net/hurry0808/article/details/78573585?utm_source=copy 

 

步骤：

1、导入模块：pandas、matplotlib

2、读取数据

3、为项目设置matplotlib参数

　　设置参数有两种方法：调用命令matplotlib.rc()；通过传入关键字元组，修改参数

　　　　　　　　　　　　使用参数字典：matplotlib.rcparams；

 

　　为了能让matplotlib能正常显示中文和能正常显示符号，需调用以下语句　

　　　　matplotlib.rcParams['font.sans-serif']=['SimHei']   #用来正常显示正文

　　　　matplotlib.rcParams['axes.unicode_minus']=False    #用来正常显示负号

4、使用scatter_matrix画图　

 1 import pandas
 2 import matplotlib
 3 
 4 data=pandas.read_csv(
 5             "C:\\Users\\Jw\\Desktop\\python_work\\Python数据挖掘实战课程课件\\4.3\\data.csv")
 6 
 7 x=data[["等级"]]
 8 y=data[["资源"]]
 9 
10 font={
11       "family":"SimHei"}
12       
13 matplotlib.rc('font', **font);
14 matplotlib.rcParams["axes.unicode_minus"]=False
15 
16 from pandas.tools.plotting import scatter_matrix
17 
18 scatter_matrix(
19         data[["等级", "资源"]],
20         alpha=0.8,figsize=(10,10),diagonal="kde")

 

2、根据得到的图形与已经的模型对比

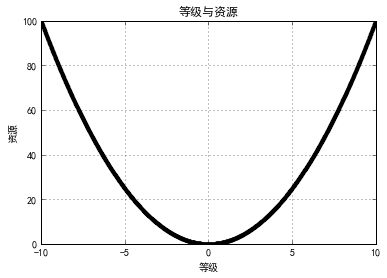
 scatter_matrix得到的kde图符合一元二次方程，与一元二次方程进行对比

 1 import numpy;
 2 x_ = numpy.arange(-10, 10, 0.01);
 3 y_ = x_**2
 4 
 5 from matplotlib import pyplot as plt;
 6 
 7 plt.figure();
 8 plt.title('等级与资源')
 9 plt.xlabel('等级')
10 plt.ylabel('资源')
11 plt.grid(True)
12 plt.plot(x_, y_, 'k.')
13 plt.show()

与scatter_matrix得到的相符合，degree设置为2

3、使用PolynomialFeaturess来构建特征

它是使用多项式的方法来进行的，如果有a，b两个特征，那么他的2次多项式为(1，a，b，a^2，b^2)

PolynomialFeatures有三个参数：

　　degree：空值多项式的度

　　interaction_only:默认为False，如果指定为True，那么就不会有特征自己和自己结合的项，上面的二次项中没有a^2，b^2

　　include_bias:默认为True，如果为True的话，就会有上面的1 那一项

 

解决方法:

把一元非线性方程转化为多元一次方程；

确定了一元非线性方程中的n，就可以作为degree传入PolynomialFeatures类；

预测的时候不能直接使用转换前的因变量作为参数传入模型，需要fit_transform转换才能进行预测

 1 from sklearn.linear_model import LinearRegression
 2 from sklearn.preprocessing import PolynomialFeatures
 3 
 4 
 5 pf=PolynomialFeatures(degree=2)
 6 x_2_fit=pf.fit_transform(x)  #一元二次的方程就转化为二元一次的方程
 7 
 8 lrModel=LinearRegression()
 9 lrModel.fit(x_2_fit,y)
10 
11 lrModel.score(x_2_fit,y)    #模型拟合程度
12 
13 x_2_predict=pf.fit_transform([[21],[22]])
14 lrModel.predict([[21],[22]])

 

小结：

一元n次方程，转换为多元线性方程：

　　pf=sklearn.preprocessing.PolynomialFeatures(degree=2)

转换方法：

　　x_2_fit=pf.fit_trasform(x)

预测：

　　LinearRegression().predict(x_2_fit)

转载于:https://www.cnblogs.com/U940634/p/9741922.html