深度增强学习（DRL）漫谈 - 从AC（Actor-Critic）到A3C（Asynchronous Advantage Actor-Critic）

前言

之前在文章《深度增强学习（DRL）漫谈 - 从DQN到AlphaGo》扯了一些关于DRL的内容，但因为是以DQN为主线，其中大部分谈的是value-based方法。我们知道传统增强学习（Reinforcement learning, RL）中除了value-based方法，还有一大类就是policy-based方法。在RL任务中，我们本质上最终要学习的是策略（Policy）。前者用的是间接方法，即通过学习值函数（value function）或者动作值函数（action-value function）来得到policy。而后者是直接对policy进行建模和学习，因此后者也称为policy optimization。Policy-based方法又可分为两大类：gradient-based方法和gradient-free方法。前者也称为policy gradient（PG）方法。而policy gradient方法又可细分为几类，如finite difference，Monte-Carlo和Actor-Critic等。Actor-Critic（AC）方法其实是policy-based和value-based方法的结合。因为它本身是一种PG方法，同时又结合了value estimation方法，所以有些地方将之归为PG方法的一种，有些地方把它列为policy-based和value-based以外的另一种方法，都好理解。在AC框架中，actor负责policy gradient学习策略，而critic负责policy evaluation估计value function。可以看到，一方面actor学习策略，而策略更新依赖critic估计的value function；另一方面critic估计value function，而value function又是策略的函数。Policy和value function互为依赖，相互影响，因此需要在训练过程中迭代优化。这种多元优化的迭代思想其实在机器学习中有很多体现。

有了critic和actor的概念，再看当时其它的方法，就可以分为critic-only方法和actor-only方法两类。前者基于value estimation。它广泛应用于各种领域，但有一些缺点使它的应用受到局限。如 1） 比较难应用到随机型策略（stochastic policy）和连续的动作空间。2） value function的微小变化会引起策略变化巨大，从而影响训练收敛性。尤其是引入函数近似（function approximation，FA）后，虽然算法泛化能力提高了，但也引入了bias，从而使得训练的收敛性更加难以保证。而后者通过将策略参数化，从而直接学习策略。这样做的好处是与前者相比拥有更好的收敛性，以及适用于高维连续动作空间及stochastic policy。但缺点包括梯度估计的variance比较高，且容易收敛到非最优解。另外因为每次梯度的估计不依赖以往的估计，意味着无法充分利用老的信息，因此数据利用率低。

可以看到，两类方法各有利弊，而AC算法结合了两者的优点。其实AC的历史其实非常悠久。反直觉地，它比critic-only和actor-only方法更早。我们知道，学术中很多时候一般是先有了牛逼算法A，再有了牛逼算法B。但A，B算法一般都有缺点，于是有一天有人将两者整合，结合了两者优点，避免了两者缺点，皆大欢喜，喜大普奔。但对于AC算法来说其架构可以追溯到三、四十年前。 最早由Witten在1977年提出了类似AC算法的方法，然后Barto, Sutton和Anderson等大牛在1983年左右引入了actor-critic架构。但由于AC算法的研究难度和一些历史偶然因素，之后学界开始将研究重点转向value-based方法。之后的一段时间里value-based方法和policy-based方法都有了蓬勃的发展。前者比较典型的有TD系的方法。经典的Sarsa, Q-learning等都属于此列；后者比如经典的REINFORCE算法。之后AC算法结合了两者的发展红利，其理论和实践再次有了长足的发展。直到深度学习（Deep learning, DL）时代，AC方法结合了DNN作为FA，产生了化学反应，出现了DDPG，A3C这样一批先进算法，以及其它基于它们的一些改进和变体。可以看到，这是一个先分后合的圆满故事。

理论背景

前面主要简略瞎扯了AC算法相关的发展史。下面罗列下本文涉及的几篇论文的主要相关理论背景。前面也提到，PG方法是一大类基于梯度的策略学习方法。经典的REINFORCE算法和AC算法都可以纳入其框架。我们就以它开始。其基本做法是先定义policy为参数$\theta$的函数，记作$\pi (\theta )$，然后定义$J(\theta )$为目标函数（Objective function，or performance objective），接着通过利用目标函数相对于参数的梯度更新参数$\theta$，从而达到目标函数的局部最大值。记作：
$$\Delta \theta =\alpha {\nabla }_{\theta }J(\theta )$$
在Sutton的奠基性论文《Policy Gradient Methods for Reinforcement Learning with Function Approximation》中证明了结合可微FA的PG方法可收敛到局部最优点。论文中提出了两种objective function定义，但结论是一致的 。以average reward formulation为例，它把$J$定义为平均回报（average reward），对其求导，得到了(Stochastic) Policy Graidient定理。详细证明请见论文附录。其核心结论给出了目标函数相对于策略参数的梯度公式：
$$\frac{\partial J(\theta )}{\partial \theta }=\sum _s{d}^{\pi }(s)\sum _a\frac{\partial \pi (s,a)}{\partial \theta }{Q}^{\pi }(s,a)$$
重点是它其中不含有状态稳态分布$d^{\pi }(s)$对于策略参数的导数，这意味着参数的变化对于状态稳态分布没有影响，这样有利于通过采样来逼近和估计梯度。因为这样的话通过执行策略$\pi$来得到状态的分布就可以得到无偏估计。注意如果其中的$Q$函数用真实的累积回报来估计，那就是REINFORCE算法。但结合了FA，即$Q_w(s,a)$后，会引入bias。因此Sutton还证明了如果FA是compatible的，那就不会有bias。但注意机器学习bias只是一方面，因为error=bias+variance。因此即使no bias，但variance大，算法收敛不了，那也白瞎。后面会看到一些减小variance的方法。

曾经有一段时间大家普遍认为online的TD方法在有linear FA时只有在on-policy情况下才有收敛性保证。而off-policy方法（如Q-learning）虽然在tabular情况下可以保证收敛，但是在有linear FA情况下就无法保证收敛。而least-squares方法（如LSTD, LSPI）虽能解决off-policy和linear FA下的收敛性问题，但计算复杂度比较高。Sutton和Maei等人提出的GTD（Gradient-TD）系方法（如Greedy-GQ）解决了off-policy，FA，online算法的收敛性问题。它最小化目标MSPBE（mean-squared projected Bellman error），通过SGD优化求解。但因为它仍是TD方法，因此仍然逃不了TD方法在上面提到的固有缺点。要避免这些缺点，一般的做法是用PG算法（如AC算法）。在Degris等人的论文《Off-Policy Actor-Critic》中将AC算法扩展到off-policy场景，提出了OffPAC算法，它是一种online, off-policy的AC算法。 OffPAC中的critic部分采用了上面提到的GTD系方法-GTD(λ)算法。

相关论文选读

好了，下面看下目前业界比较领先的DRL算法-A3C算法。我们先来看下其它两篇近年AC发展历史中比较重要的论文，最后再来看A3C算法。

• ICML 2014 DeepMind 《Deterministic Policy Gradient Algorithms》

这篇文章主要提出了用于连续动作空间的deterministic policy gradient(DPG)定理，和一种学习确定性目标策略（Deterministic target policy）的off-policy AC算法。回忆之前的stochastic policy ${\pi }_{\theta }(a|s)$ 定义为动作的分布。而deterministic policy则为状态到动作的映射$a={\mu }_{\theta }(s)$。背后的基本思想是，虽然policy可以用概率分布表示，但我们想要的其实就是一个动作而已。以往一般认为deterministic policy gradient不存在，而这篇论文将PG框架推广到deterministic policy，证明了deterministic policy gradient不仅存在，而且是model-free形式且是action-value function的梯度，形式简单。Deterministic Policy Gradient（DPG）定理给出了目标函数对于策略参数的梯度：
$${\nabla }_{\theta }J({\mu }_{\theta })={\int }_{\mathcal{S}}{\rho }^{\mu }(s){\nabla }_{\theta }{\mu }_{\theta }(s){\nabla }_a{Q}^{\mu }(s,a){|}_{a={\mu }_{\theta }(s)}ds$$

并且证明了它是之前stochastic policy gradient定理当policy的variance趋向于0时的极限。这意味着compatible FA，natural gradients等一众理论都可以应用到DPG场景。用stochastic policy gradient算法时，当学习进行到后期，policy的分布的variance变小。因为policy对其参数的导数在均值附近会变得非常大（比如高斯分布），从而导致变化很大。另外，在高维动作空间问题中，stochastic policy gradient定理中的梯度内积需要在高维空间中采样，而deterministic policy gradient不需要积分，有解析解。这些都是引入deterministic policy后带来的好处。

但deterministic policy又会导致exploration不足。解决方案是选择动作时用stochastic behavior policy，而学习目标为deterministic target policy。这就意味着需要off-policy。定义behavior policy $\beta (a|s)$，target policy为${\pi }_{\theta }(a|s)$。这off-policy和stochastic policy下，根据论文《Off-Policy Actor-Critic》中的结论，performance objective和其对于$\theta$的梯度可写为：
$${\nabla }_{\theta }{J}_{\beta }({\pi }_{\theta })\approx {\mathbb{E}}_{s\sim {\rho }^{\beta },a\sim \beta }\frac{{\pi }_{\theta (a|s)}}{{\beta }_{\theta }(a|s)}{\nabla }_{\theta }\log {\pi }_{\theta }(a|s)Q^{\pi }(s,a)]$$
对应的OffPAC算法中crtic部分用了gradient TD方法。Actor和critic是基于target policy，通过importance sampling进行估计。

接下来，理论指导实践，该论文根据DPG定理论文提出了deterministic AC算法。先是基于on-policy(Sarsa)和off-policy（Q-learning）情况提出了deterministic AC算法，然后基于OffPAC算法提出了OPDAC（off-policy deterministic actor-critic algorithm）算法。OPDAC算法将前面的OffPAC中的梯度公式扩展到deterministic policy，给出off-policy deterministic policy gradient：
$${\nabla }_{\theta }{J}_{\beta }({\mu }_{\theta })\approx {\mathbb{E}}_{s\sim {\rho }^{\beta }}[{\nabla }_{\theta }{\mu }_{\theta }(s){\nabla }_a{Q}^{\mu }(s,a){|}_{a={\mu }_{\theta }(s)}]$$
但它们自然不是最牛的，就和电影一样，是为了将剧情一波一波推向高潮，大boss总是最后出来的。前面这些只是作为更清楚解释原理的引子 。它们都有收敛性问题（因为FA引入的bias和off-policy引入的不稳定性），于是论文最后放出大招，结合compatible FA和gradient TD给出了COPDAC-GQ算法。

• ICLR 2016 DeepMind 《Continuous Control with Deep Reinforcement Learning》

之前是前DL时代的研究。近年来随着DL的兴起，PG进入DL时代就成了必然趋势了。我们看到value-based方法已和DQN结合产生了DQN，而DL在其中其实主要充当了FA的角色。而另一方面PG中也需要FA，那PG和DL的结合也很自然了。这篇论文提出model-free, off-policy，actor-critic的DRL算法。称为Deep DPG，即DDPG算法 。我们知道原始的DQN无法应用到连续动作空间。直觉上当然可以通过离散化动作空间解决，但会导致维度灾难（curse of dimensionality）。DDPG基于DPG算法，它将AC方法与DQN结合。回顾一下DQN的理论意义，在它之前，学术界普遍认为大型非线程FA用于学习value function或者action-value function理论上收敛不可保证，且实际学习效果也不稳定。不用大型非线性FA，算法又扩展不到大型状态空间，只能在小规模场景中用用，没啥意思，用了么又没收敛性保证，挺尴尬的。而DQN有力地推翻了这个认识，这才是DQN比较大的理论贡献。它证明了用非线程FA来表示value function也可以稳定收敛。当然这很大程度上归功于replay buffer和target Q network。前者直观上就是让observation（或称为sample, experience）不要立即用于更新，而是存下来再从中随机选取来更新，从而解决了sample之间相互关联的问题；后者作用上起到参数更新的平滑作用，即不是基于sample更新参数后立即生效，而是通过"soft"的方式更新到目标网络（通过参数$\tau$控制其比例）。从而解决了Q函数更新的发散问题，使训练过程更加稳定。DDPG同样用到了这两大法器，同时再加上2015年Ioffe和Szegedy提出的batch normalization（它是DNN优化上general的方法，在DNN的优化中广泛应用）。在一些问题，尤其是低维问题中，不同的components的物理单位是不同，或者说相差很大。这会影响学习效率和使通用超参数学习更困难。面对这种不同状态不同分量scale不同的问题第一反应当然是normalization。一种是在input feature阶段就做scale，另一种就是batch normalization。它维护mean和variance的running average，将每一维度在minibatch中的sample间进行normalization，使它们有unit mean & variance。该方法减少了深度网络训练过程中的covariance shift，使得算法可以更好地适应各种不同任务，处理各种不同类型输入。

综合以上方法，DDPG算法（具体参见论文中的Algorithm 1）将DPG中的linear FA扩展到nonlinear FA，即DNN，并使之适用于online情况和高维状态和动作空间。

另外还有就是连续动作空间中的exploration问题。这里使用了加一个noise process中产生的noise sample到actor policy来得到 exploration policy（也就是behaviour policy）。

算法中actor和critic均用DNN表示，分为称为actor network和critic network。它们分别是deterministic policy $\mu$和value-action function $Q$的FA，参数分别为${\theta }^Q$和${\theta }^{\mu }$。在维度比较低时，有下面的结构：

而当输入为image（即raw pixels）时，按套路需要加卷积层和全连接层（这里是3层Conv，2层FC）来学习特征。这里用的深度网络优化方法为Adam optimizer（当前DNN主流优化算法之一）。在迭代更新过程中，先积累experience replay buffer直到达到minibatch指定个数，然后根据sample分别更新两个DNN。先更新critic，通过loss函数$L$更新参数${\theta }^Q$。然后，通过critic得到$Q$函数相对于动作$a$的梯度，因为在actor的更新公式（也就是DPG定理）中会用到，然后应用actor更新公式更新参数。刚才得到的${\theta }^{\mu }$和${\theta }^Q$，对于$\theta$的更新，会按比例（通过参数$\tau$）更新到target network。这个target network会在下一步的训练中用于predict策略和$Q$函数值。

这篇文章主打解决高维连续动作控制问题，最大的特点就是简单。实验包括cartpole swing-up, dexterous manipulation, legged locomotion和car driving（Torcs）等各种控制场景。

• ICML 2016 DeepMind 《Asynchronous Methods for Deep Reinforcement Learning》

这篇论文中提出了A3C（asynchronous advantage actor-critic）算法。它不仅适用于离散也适用于连续动作空间的控制问题。这是2016提出的方法，到现在已有不少基于该算法的改进，但基本思想和框架没有大改，如今仍是最牛逼的DRL算法之一。之前一想到DRL，言必集群，言必GPU，不提这些不好意思跟人打招呼。当然，DRL领域也确实有很成功的分布式机器学习系统，比如Google的Gorila。这篇文章另辟蹊径，发明了“平民版”的DRL算法，证明了我们这些架不起集群，买不起GPU的穷人也照样能玩转前沿高端科技，而且效果还不比前者差。

传统经验认为，online的RL算法在和DNN简单结合后会不稳定。主要原因是观察数据往往波动很大且前后sample相互关联。像Neural fitted Q iteration和TRPO方法通过将经验数据batch，或者像DQN中通过experience replay memory对之随机采样，这些方法有效解决了前面所说的两个问题，但是也将算法限定在了off-policy方法中。本文提出了另一种思路，即通过创建多个agent，在多个环境实例中并行且异步的执行和学习。于是，通过这种方式，在DNN下，解锁了一大批online/offline的RL算法（如Sarsa, AC, Q-learning）。它还有个潜在的好处是不那么依赖于GPU或大型分布式系统。A3C可以跑在一个多核CPU上。总得来说，这篇论文更多是工程上的设计和优化。另外，将value function的估计作为baseline可以使得PG方法有更低的variance。这种设定下，$R_t-b_t(s_t)$，即$A(s_t,s_t)=Q(a_t,s_t)-V(s_t)$就是advantage function的估计。这也是A3C名字中其中一个A - advantage的由来。

这篇文章将one-step Sarsa, one-step Q-learning, n-step Q-learning和advantage AC扩展至多线程异步架构。注意这几种方法特点迥异，AC是on-policy的policy搜索方法，而Q-learning是off-policy value-based方法。这也体现了该框架的通用性。简单地说，每个线程都有agent运行在环境的拷贝中，每一步生成一个参数的梯度，多个线程的这些梯度累加起来，一定步数后一起更新共享参数。它有几个显著优点：1）它运行在单个机器的多个CPU线程上，而非使用parameter server的分布式系统，这样就可以避免通信开销和利用lock-free的高效数据同步方法（Hogwild!方法）。2）多个并行的actor可以有助于exploration。在不同线程上使用不同的探索策略，使得经验数据在时间上的相关性很小。这样不需要DQN中的experience replay也可以起到稳定学习过程的作用，意味着学习过程可以是on-policy的。其它好处包括更少的训练时间，另外因为不需要experience replay所以可以使用on-policy方法（如Sarsa），且能保证稳定。

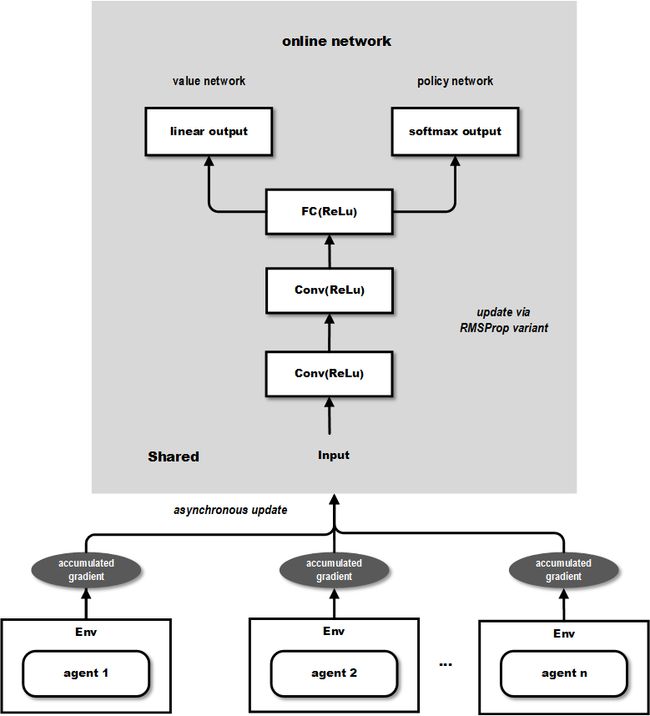
在这篇文章中提出的几种算法中主打的是A3C（asynchronous advantage actor-critic）算法（具体参见论文中的Algorithm S3）。该算法和DDPG类似，通过DNN维护了policy和value function的估计，但它没用deterministic policy。在学习过程中使用n-step回报来同时更新policy和value function。网络结构使用了CNN，其中一个softmax output作为policy $\pi (a_t|s_t;\theta )$，而另一个linear output为value function $V(s_t;{\theta }_v)$，其余layer都共享。另外，作者还发现一个古老的技巧，即将policy的entropy加到目标函数可以避免收敛到次优确定性解。直观上，加上该正则项后目标函数更鼓励找entropy大的，即形状“扁平”的分布，这样就不容易在训练过程中聚集到某一个动作上去。在优化方法上，作者使用了基于RPMProp的一种变体。整个过程大致如图

作者在Atari 2600（游戏模拟器），TORCS（赛车游戏），MoJoCo（物理模拟器，连续动作空间电机控制任务）和Labyrinth（随机生成的迷宫）这几个平台上做了实验。 实验证明在Atari的一些游戏中n-steps方法比one-step方法快，这个好理解。另外policy-based advantage actor-critic方法比value-based method牛逼些。实验中通过6个游戏学习了超参数，然后在其它57个游戏中固定这些参数，证明了算法的通用性。如前面所说，A3C通过并行使得计算效率提升，可以用CPU达到之前用GPU达到的训练效率。使用了16 core的CPU只用了1~4天，而其它方法用了Nvidia K40 GPU，还训练了8~10天。而A3C只用了其它方法一半的训练时间就在57个游戏中超过了其它方法的平均得分。

Labyrinth非常有挑战之处在于它每次episode都会生成一个新的迷宫，所以学习到的策略必须够general。显然，走迷宫和MuJoCo不像前面的任务（Atari, TORCS都是反应式的，即看着当前的画面，就能得到最优策略），它更需要“记忆”。因此这里A3C也使用了RNN（在最后的hidden layer后加了额外的256个LSTM cell）。接下来，论文讨论了算法的scalability。毕竟我们知道对于多线程方法，最怕的是线程是开了一坨，结果由于数据依赖或是其它原因并行不起来，那就白瞎了。但既然是牛方法，自然不会差。结果显示当工作线程增多时，算法可以获得显著的加速。16个线程的时候，就加速一个数量级了。而且在一些算法中（如one-step Q-learning和Sarsa）还达到了不科学的超过线性的加速比。当然，这样的严肃出版物中怎么能有不科学的东西呢，作者们用多线程减少了one-step方法的有偏性来解释了这一现象。可以看到，这论文里做的实验很充分。总而言之，言而总之，从实验数据可以看到，A3C方法，无论是离散还是连续动作空间问题，都完爆前面的state-of-the-art方法就对了。