二进制及原码反码补码介绍、八进制、十六进制及Java中移位运算详解

1.二进制

二进制，是计算技术中广泛采用的一种数制，二进制数据是用0和1两个数码来表示的数。它的基数为2，进位规则是“逢二进一”，借位规则是“借一当二”。

二进制的最高位是符号位，0是正数，1是负数，所以8位二进制的取值范围用二进制表示是[11111111,01111111]，用十进制表示是[-128,127]，二进制中约定正数的原码反码补码相同。
java中二进制表示为0b开头，如

    int b = 0b00010001;//对应十进制为2的4次方+2的0次方=17

8位最大的二进制有符号数对应的十进制计算规则如下：

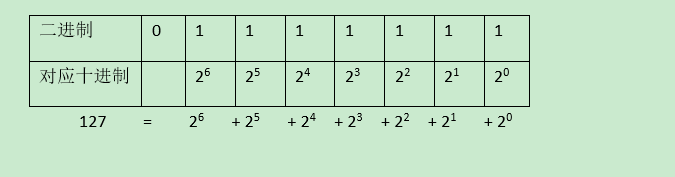
再举个例子，将0b00010101转换为十进制，计算规则如下：

0b00010101 => 2⁴ +2² +2⁰ = 16 + 4 + 1 = 21

1.1.原码

原码即二进制本身

1.2.反码

正数的反码与原码相同；
    如：00001000 反码为 00001000
负数保持符号位为1，其他位按位取反得到的即是负数的反码；
    如：10001000 反码为 11110111

1.3.补码

正数的补码与原码、反码相同；
    如：00001000 补码为 00001000
负数的补码为反码+1
    如：10001000 反码为 11110111 ，则它的补码为 1 111 0111 +0 000 0001 = 1 1111000，即它的补码为11111000

1.4.浮点数的二进制与十进制转换

• 二进制转十进制

0101.011 ==> 1=0*2³ + 1*2² + 0*2¹ + 1*2⁰ + 0*1/2¹ + 1*1/2² + 1*1/2³ ==> 5.375

• 十进制转二进制

整数部分采用"除2取余，逆序排列"法。具体做法是：用2整除十进制整数，可以得到一个商和余数；再用2去除商，又会得到一个商和余数，如此进行，直到商为小于1时为止，然后把先得到的余数作为二进制数的低位有效位，后得到的余数作为二进制数的高位有效位，依次排列起来。
小数部分采用"乘2取整，顺序排列"法。具体做法是：用2乘十进制小数，可以得到积，将积的整数部分取出，再用2乘余下的小数部分，又得到一个积，再将积的整数部分取出，如此进行，直到积中的小数部分为零，此时0或1为二进制的最后一位。或者达到所要求的精度为止。

如将6.125转换为二进制

• 处理正数部分
  6/2=3 ----> 余0
  3/2=1----->余1
  1/2=0----->余1
  即正数部分为110
• 处理小数部分
  0.1252=0.25 ----->整数位为0
  0.252=0.5 ----->整数位为0
  0.5*2=1.0 ----->整数位为1
  即小数部分为001
  即最终结果为110.001

2.八进制

八进制的数据是用0,1,2,3,4,5,6,7来表示，它的基数是8，逢8进1。
java中八进制表示为0开头，如：

   int c = 0023;//对应十进制为2*8的1次方+3*8的0次方=19

4位最大的八进制数对应的十进制计算规则如下：

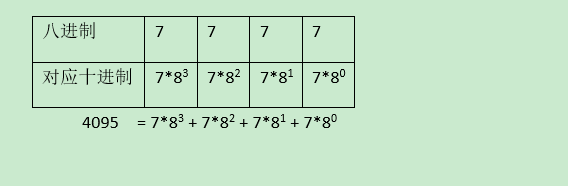
再举个例子，将0235转换为十进制，计算规则如下：

0235=> 2*8² +3*8¹ +5*8⁰ = 128 + 24 + 5 = 157

3.十六进制

十六进制的数据是用0,1,2,3,4,5,6,7,8,9,a,b,c,d,e,f来表示，它的基数为16，逢16进1。
java中十六进制表示用0x开头，如：

    int d = 0x1ed;//对应16进制为1*16的2次方+14*16的1次方+15*16的0次方=493

16进制基础值对应的十进制为：

4位最大的十六进制数对应的十进制计算规则如下：

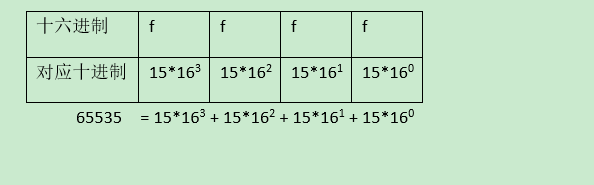
再举个例子，将0xe3f转换为十进制，计算规则如下：

0xe3f=> 14*16² +3*16¹ +15*16⁰ = 3584 + 48 + 15 = 3647

4.位运算

4.1.位运算规则

• 所有的位运算都是补码之间的运算
• 所有的位运算得到的都是补码，需要将补码转换为原码才是最终结果
• 正数的原码与反码补码相同，负数的原码为补码-1之后再取反码

4.2.与（&）运算

二进制中两个操作数都为1,结果才为1，即：
1 & 1 = 1
1 & 0 = 0
0 & 1 = 0
0 & 0 = 1
将两个操作数转换为二进制后，进行按位与运算。如：

56 & 78 => 00111000 & 01001110 = 00001000 = 8

4.3.或（|）运算

二进制中两个操作数至少有一个为1,结果才为1，即：
1 | 1 = 1
1 | 0 = 1
0 | 1 = 1
0 | 0 = 0
将两个操作数转换为二进制后，进行按位或运算。如：

56 | 78 => 00111000 | 01001110 = 01111110 = 126

4.4.非（~）运算

非运算是二进制中对每个操作数取反，即~0=1，~1=0，二进制数经过非运算后得到是补码，如果结果是正数（最高位为0）则补码即是原码，如果结果是负数（最高位为1）则需要将补码转换为原码如：
35 对应的二进制为 00100011
~00100011结果为 11011100 最高位是1即为负数，需要将此补码转换为原码，负数的原码计算规则为 补码-1然后取反码，先将补码-1即11011100 -1 = 11011011，再按位取反，即10100100 = 36，故~35 = -36

4.5.异或（^）运算

二进制中两个操作数相同为0,两个操作数不同为1，即：
1 ^ 1 = 0
1 ^ 0 = 1
0 ^ 1 = 1
0 ^ 0 = 0
将两个操作数转换为二进制后，进行按位异或运算。如：

56 ^ 78 => 00111000 ^ 01001110 = 01110110 = 118

4.6.移位（<<   >>   >>>）运算

4.6.1 <<运算符

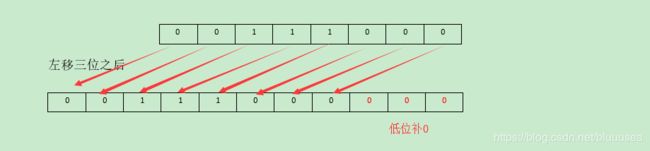
左移运算符，将对象转换为二进制后每个操作数向左移动指定位数，低位补0

56 << 3 ==> 00111000 << 3 ==> 001 11000000 ==> 2⁸ + 2⁷ + 2⁶ = 448

过程如下：

4.6.2 >>运算符

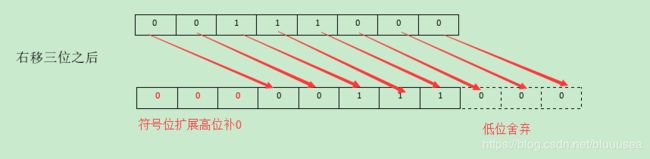
有符号右移运算符，将对象转换为二进制后每个操作数向右移动指定位数，采用符号位扩展机制：正数（符号位为0）高位补0；负数（符号位为1）高位补1

• 正数的有符号右移运算如下：

56>>3 ==> 00111000 >> 3 ==>00000111 ==> 7
过程如下：

• 负数的有符号右移运算如下：

-56 >> 3
-56原码为10111000，先转为补码为11001000，再将补码右移2位（高位）结果为11111001，
得到的补码为负数，需要将此补码转换为原码，即先-1再取反码，即
11111001 - 1 =11111000 再取反码为 10000111 ，即最终结果为-7

4.6.3 >>>运算符

无符号右移运算符将对象转换为二进制后每个操作数向右移动指定位数，无论正数负数都是高位补0，所以正数的有符号右移运算和无符号右移运算结果相同，负数的有符号右移运算和无符号右移运算结果不同。无符号右移运算仅对32位和64位有意义，因为在表达式中较小的值会自动提升为int值，这意味着符号扩展并且位移只发生在32位值上而不是8位或16位值上。

• 正数的无符号移位运算如下：

56>>>3 ==> 00111000 >>> 3 ==>00000111 ==> 7

• 负数的无符号右移如下：

-56 >>> 3
-56原码为10111000，先转为补码为11001000，再将补码右移3位，因为高位补0并且会自动转换为int值即32位，因此需要将32位补码全部修改，故右移后得到的值为00011111 11111111 11111111 11111001，最高位为0即为正数，即原码与补码相同，故最终结果为 2²⁸ + 2²⁷ + 2²⁶ + … + 2⁵ + 2⁴ + 2³ + 2⁰ = 2²⁹ - 2² - 2¹ = 536870905

5.java中基础类型取值范围

java虚拟机中一个字节占用8位，其中short占用2字节，int占用4字节，long占用8字节。

• short占用2个字节，即二进制位16位，其中最高位为符号位，则short的取值范围二进制为[11111111 11111111,01111111 11111111]，十进制为[-2¹⁵, 2¹⁵-1]
• int占用4个字节，即二进制位32位，其中最高位为符号位，则int的取值范围二进制为[11111111 11111111 11111111 11111111,01111111 11111111 11111111 11111111]，十进制为[-2³¹, 2³¹-1]
• long占用8个字节，即二进制位64位，其中最高位为符号位，则long的取值范围十进制为[-2⁶³, 2⁶³-1]
• float占用4个字节，即二进制32位，其中1位符号位，8位指数位即指数位即指数最大值为2⁷-1=127，23位小数部分尾数，即float最大值为2¹²⁸-1
  
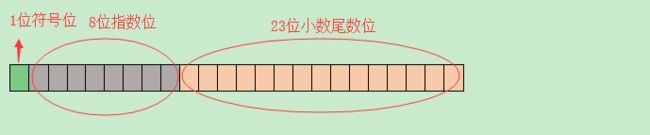
• double占用8字节，即二进制64位，其中1位符号位，11位指数位即指数最大值为2¹⁰-1=1023，52位小数部分尾数，即double最大值为2¹⁰²⁴-1