【图表示学习】word2vec与DeepWalk
一、word2vec
在自然语言处理中,词向量是一种常见的词分布式表示。词表中的每个单词均由一个维度固定的连续向量表示。word2vec是2013年Google公布的训练词向量的工具,其包含了两个模型,分别是:CBOW和SkipGram。这里仅简单介绍SkipGram模型,更加详细的原理介绍见文章【自然语言处理】【Word2Vec(二)】超详细的原理推导(包含负采样和层次softmax)。
1. SkipGram模型结构
如果词表为V,那么SkipGram就是某个单词的one-hot编码,其是一个维度为|V|的向量。其结构如图所示
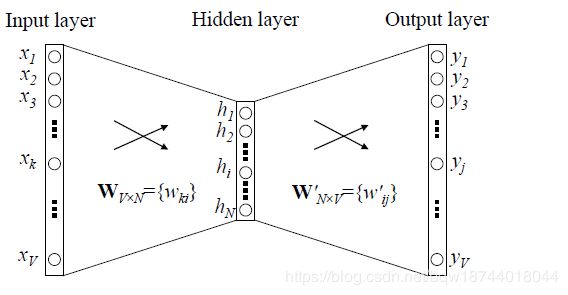
该模型可以看做是不带激活函数的双层全连接神经网络。更正式的来说,输入向量 x ∈ R ∣ V ∣ x\in\mathbb{R}^{|V|} x∈R∣V∣,输入层权重为 W ∈ R V × N W\in\mathbb{R}^{V\times N} W∈RV×N,输出层权重为 W ′ ∈ R N × V W^{'}\in\mathbb{R}^{N\times V} W′∈RN×V。其前向传播过程中,输入层到隐藏层为
h = W T x ∈ R N h=W^Tx\in\mathbb{R}^N h=WTx∈RN
隐藏层到输出层为
u = W ′ T h ∈ R V u=W^{'T}h\in\mathbb{R}^V u=W′Th∈RV
使用softmax层转换为概率分布
y = softmax ( u ) ∈ R V y=\textbf{softmax}(u)\in\mathbb{R}^V y=softmax(u)∈RV
2. SkipGram主要思想
SkipGram的主要思想是使用输入词来预测上下文。举例来说,给定一个句子"Named entity recognition plays an important role"。那么在一次训练中输入为单词"recognition",需要预测的是其上下文单词"Named"、“entity”、“plays”、“an”。SkipGram的最终目标是获得输入层到隐藏层的权重矩阵 W W W,其大小为 V × N V\times N V×N。由于 W W W是由V个N维向量组成,每个向量就对应词表中的一个词。所以 W W W就是词表V中单词的词向量集合。
3. SkipGram训练过程
上面说“使用输入词来预测上下文”,但是模型结构决定其不能同时预测多个上下文。因此在实际的训练过程当中,依次使用输入词预测上下文单词。例如,使用“recogniton”预测“Named”,然后使用“recogniton”预测“entity”,再使用“recogniton”预测“plays”,最后使用“recogniton”预测“an”。常见的SkipGram的结构图如下图,但其实该图是SkipGram结构图和训练过程的结合。

4. 层次Softmax
通常来说,词表的大小|V|会十分的巨大,在计算softmax时需要进行幂运算,因此计算量十分巨大。层次softmax就是为了解决这个问题,将原始的时间复杂度 O ( ∣ V ∣ ) O(|V|) O(∣V∣)降低至 O ( l o g ∣ V ∣ ) O(log|V|) O(log∣V∣)。
原始softmax可以将输入转换为概率分布,而层次softmax则是将|V|个单词的概率值分配到二叉树的叶节点上。其结构如下图

词表中的|V|个单词,分别是 w 1 , w 2 , … , w V w_1,w_2,\dots,w_V w1,w2,…,wV。该树中的每个非叶节点都对应一个线性二分类器(也就是逻辑回归LR),也就是说每个叶节点都有一个需要进行学习的参数。那么,这个树是如何替代原始softmax来表示某个词的概率呢?由于每个非叶节点的分类器都会输出一个概率值,某个词的概率就是由根节点到对应词路径上的所有概率乘积来表示的。举例来说,前向传播过程中预测单词 w 2 w_2 w2的概率,则是由节点 n ( w 2 , 1 ) n(w_2,1) n(w2,1)预测为左的概率 P ( n ( w 2 , 1 ) , l e f t ) P(n(w_2,1),left) P(n(w2,1),left)乘以节点 n ( w 2 , 2 ) n(w_2,2) n(w2,2)预测为左的概率 P ( n ( w 2 , 2 ) , l e f t ) P(n(w_2,2),left) P(n(w2,2),left),再乘以节点 n ( w 2 , 3 ) n(w_2,3) n(w2,3)预测为右是概率 P ( n ( w 2 , 3 ) , r i g h t ) P(n(w_2,3),right) P(n(w2,3),right)来决定的,即 w 2 w_2 w2为目标输出词 w o w_o wo的概率为
P ( w 2 = w o ∣ w i ) = P ( n ( w 2 , 1 ) , l e f t ) × P ( n ( w 2 , 2 ) , l e f t ) × P ( n ( w 2 , 3 ) , r i g h t ) P(w_2=w_o|w_i)=P(n(w_2,1),left)\times P(n(w_2,2),left)\times P(n(w_2,3),right) P(w2=wo∣wi)=P(n(w2,1),left)×P(n(w2,2),left)×P(n(w2,3),right)
之后只要使用最大似然估计来更新所有参数即可。这里再做几点说明
- 原始softmax的时间复杂度为O(|V|),而层次softmax每次前向传播时仅仅需要计算树的高度log|V|个值。因此,其时间复杂度为log|V|.
- 为了使频繁出现的单词,尽量少的更新,从而进一步降低时间复杂度。可以统计各个词出现的频数,然后构造Huffman树,使得从根节点到点频繁出现单词的路径尽量短。
- 在Huffman树中,|V|个单词有|V|-1个非叶节点,那么也就会导致模型多出来|V|-1个参数需要更新。
二、DeepWalk
DeepWalk是一种图嵌入方法,其可以将图中的顶点转换为固定维度的向量,这个向量可以捕获到该顶点的结构信息,并用于后续的顶点分类、聚类等问题。
1. 使用随机游走(Random Walk)获取训练数据
图 G = ( V , E ) G=(V,E) G=(V,E),其中 V V V是顶点集合, E E E是边的集合。随机游走:从图中随机选择一个顶点作为开始,之后再从该顶点的邻居节点随机的选择一个作为下一个节点,依次类推可以得到一个以该节点为起始的顶点序列。那么将这些顶点序列看做是一种语料,其包含了该顶点的结构信息。
2. 使用SkipGram学习图中顶点的表示
将通过随机游走获得的顶点序列看做是自然语言中的语料,并使用SKipGram对其进行序列就能得到图中顶点的向量表示。
3.并行
由随机游走产生的顶点序列具有长尾效应。因此,当使用SkipGram训练,模型反向传播时更新会比较稀疏(即某些顶点的出现频率不会过于集中)。所以,使用异步SGD也是可以的。而且,实验也证明异步SGD对最终的效果没有显著的影响。