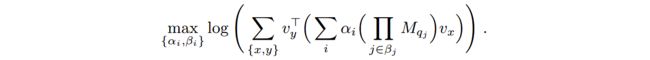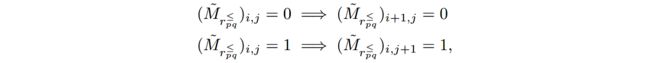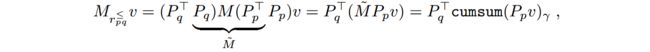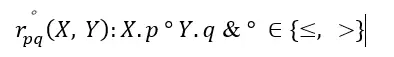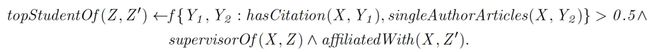【论文解读 ICLR 2020】Differentiable Learning of Numerical Rules in Knowledge Graphs

论文题目：Differentiable learning of numerical rules in knowledge graphs

论文来源：ICLR 2020 CMU, Bosch Center for AI

论文链接：https://openreview.net/forum?id=rJleKgrKwS

关键词：知识图谱，数值规则，规则的学习（抽取），知识推理

---

---

1 摘要

本文解决的是规则的学习问题，学习出来的规则可用于知识推理任务，例如链接预测等。

KG上的规则捕获了数据中可解释的模式，并且可以用于KG的清洗和补全。

可微逻辑框架TensorLog将规则推理编译成了可微的操作序列。受TensorLog的启发，最近提出的Neural LP方法可用于学习参数和规则的结构。

然而，它在处理age, weight, scicentific measurements等数字特征方面受限。本文对Neural LP进行扩展，使其能学习有数字值的规则，例如“People younger than 18 typically live with their parents”。

本文还展示了如何使用动态规划和累积和操作来确保扩展的效率。本文的方法可以实现使用聚合抽取出更具表达性的规则，并且这些规则和state-of-the-art的方法学习到的规则相比质量更高。

2 引言

链接预测是知识图谱领域的一项常见任务。大多数针对此任务的工作聚焦于规则抽取技术，近期有一些方法使用深度学习解决此任务，但是绝大多数基于深度学习的方法不具有可解释性。

Yang等人提出的Neural LP方法[1]可为链接预测任务学习到具有可解释性的规则，同时保留了学习方法的灵活性。但是Neural LP方法能表示的规则种类有限，它不能学习到依赖于数值（numerical）特征的规则。

本文提出Neural LP的扩展，可实现对数值规则的快速学习。在通用的Neural LP方法中，数值规则会导致稠密的矩阵操作，作者使用动态规划和累积求和运算，有效地表达了用于数值比较的操作符。

通过隐式地定义相关的操作符，实现了对Neural LP的扩展，使其可以有效地利用数值特征进行规则的学习，同时保留了Neural LP框架的可解释性。

在多个KG数据集上进行了实验，证明了本文的方法和Neural LP方法相比，可以更准确地回答queries，并且比state-of-the-art的规则抽取方法（AnyBurl[2]）准确率更高。在两个合成的真实数据集上进行了实验，证明了本文的方法可以依赖于数值信息更准确地恢复出规则，以实现在KG上进行更精准的链接预测。和纯图嵌入方法不同的是，本文的方法抽取出的规则仍然具有可解释性。

3 相关工作

（1）关系数据挖掘

从数据中学习规则可以看成是关系数据挖掘和归纳式逻辑编程（ILP）问题。

和本文工作最相关的是从关系数据中学习具有聚合的决策树。但是这些方法的可扩展性不好，不能处理真实世界中的KG。

在KG上进行规则的学习吸引了许多研究学者的关注，Ortona等人[3]提出的方法考虑到了带有否定词的规则，和本文的方法一样也支持数值比较。但是与本文的方法不同的是，Ortona等人的方法目的是找到一小组规则，以涵盖大多数的正例和尽可能少的负例，而本文的方法是在无监督的情况下进行规则的学习。

（2）基于神经的规则学习

有许多学者利用了嵌入模型和神经架构以进行规则的学习任务，和本文工作最相关的是Yang等人提出的方法[4]，该方法将规则学习问题简化成了对给定KG的neural-embedding-based表示进行的代数运算。但是该方法只能处理非数值型的规则。

（3）使用数值的嵌入模型

针对KG的不完备性，可以预测已有实体间的关系连边来对KG进行补全。许多方法依赖于统计并且包括张量的分解。本文的模型是基于神经嵌入的。

和本文工作最相关的是Garc´a-Dur´an和Niepert的工作[5]，他们提出了一个结合了关系、隐层和数值特征的新方法，但是该方法不具有可解释性。

4 一些定义与准备工作

（1）知识图谱

• $\mathcal{C}$为常量集合，例如实体；
• $\mathcal{N}\in \mathbb{R}$是数值（numerical values）；
• $\mathcal{R}$是二元关系，例如谓词；
• 知识图谱$\mathcal{G}$定义成有限的原子（例如 事实）集合，表示为$p(x,y)$，其中$p\in \mathcal{R},x\in \mathcal{C},y\in \mathcal{C}\cup \mathcal{N}$。例如$citedIn(john,article1)$。
• 集合${\mathcal{R}}_n\subseteq \mathcal{R}$存储了所有的数值型谓词$p$，例如$p(x,y)\in \mathcal{G},x\in \mathcal{C},y\in \mathcal{N}$。
• 数值型的事实定义为${\mathcal{G}}_n\subseteq \mathcal{G}$

使用小写字母表示常量，大写字母表示变量。

由于KG是不完备的，我们可以假定缺失的事实是未知的或者是错误的。开放世界假设（OWA）认为缺失的事实应该看成是未知的，而不是错误的。局部封闭世界假设（LCWA）则认为KG是局部完全的，缺失的事实是错误的。

（2）数值规则

规则可表示成如下的形式：

其中$p,q_1,...,q_n\in \mathcal{R}$，左边是规则头，右边是规则体，规则头或规则体中的每一个合取符可以看成是一个原子。

数值规则指的是规则中包含变量间或变量和一个数值常量间的数值比较，例如两个学者的被引用量。

为了简化表示，与$\mathcal{C}$中的某一实体相连的$\mathcal{N}$中的数值，可以看成是其“特征”，而在${\mathcal{R}}_n$中的数值关系可视为依赖于这些特征的函数。在这种情况下，对于$p(X,Y)$，还可以表示成$X.p=Y$。例如$john.hasCitation=124$是$hasCitation(john,124)$的另一种表示形式。为了简洁，$r_{pq}^{\circ }(X,Y)$代表$X.p\circ Y.q$，其中$\circ \in \{\le ,>\}$。若$p=q$，则$r_{pq}^{\circ }$下标中的第二个值可省略。

---

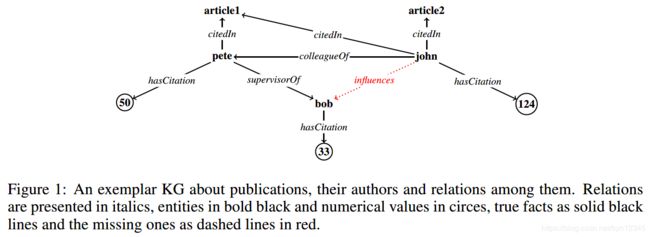
例子 1：考虑图 1所示的KG和如下的规则：

这个规则表示学生受有较高引用量的导师的同事的影响。

---

我们还可以定义一个分类关系，将特征映射为logistic分类的概率，例如$\sigma (w^{T}X.features+b)$。我们后面将讲述这样的规则可以使用Neural LP框架学习到。

（3）规则学习

给定一个知识图谱$\mathcal{G}$，规则学习的目的是从$\mathcal{G}$中抽取出规则，使得它们在$\mathcal{G}$中的应用接近于储存了所有正确的事实的理想的知识图谱。

Neural LP方法[1]就是一种规则学习的方法，它以端到端的模式并使用基于梯度的优化方法，学习到了没有比较操作符的式（1）形式的规则的分布。

Neural LP方法依赖于TensorLog框架，TensorLog将规则应用和稀疏的矩阵乘法连接了起来。在TensorLog中，所有的实体被映射为了整数，每个实体$i$都和一个one-hot向量$v_i\in \{0,1{\}}^{|\mathcal{C}|}$相关联，向量中的对应位置为1。

例如，图 1中的每个实体$c\in \mathcal{C}$都编码成了一个长度为5的0/1向量。对于每个关系$p\in \mathcal{R}$ \ ${\mathcal{R}}_n$和每个实体对$x,y\in \mathcal{C}$，定义一个矩阵$M_p\in \{0,1{\}}^{|\mathcal{C}|\times |\mathcal{C}|}$。矩阵的entry $(y,x)$定义为$(M_p)yx$，若$p(x,y)\in \mathcal{G}$，则其值为1。例如考虑图 1中的KG，对于关系$p=citedIn$，我们有：

TensorLog的思想是通过进行矩阵相乘来模拟对任意实体$X=x$应用规则，具体来说是：$M_{q_n}...M_{q_2}{M}_{q_1}{v}_x=s$，其中$v_x$表示实体$x$。向量$s$中非零的元素值指向的实体$y$表示：在$\mathcal{G}$上应用上述规则可以得到$p(x,y)$。例如，规则$influences(X,Y)\leftarrow colleagueOf(X,Z),supervisorOf(Z,Y)$的推断可以翻译成：

通过设置$v_x=[1,0,0,0,0{]}^T$做为john的指示器，并应用矩阵相乘，我们可以得到$bob$的指示器$s=[0,0,1,0,0{]}^T$。由于$M_{q_1},...,M_{q_n}$是稀疏的，可以高效地进行matrix-vector相乘操作，并在GPU上并行进行推断过程。

在Neural LP中，使用上述的操作符用于学习每个规则头：

其中$i$是所有可能规则的索引，${\alpha }_i$是和规则$r_i$相关联的可信度，${\beta }_i$是在这些规则中出现的所有关系的有序列表。规则是从如下的优化问题的解中得出的：

5 使用数值特征和否定词进行规则学习

本文的主要贡献是对Neural LP框架进行扩展，使得我们可以在规则体中使用带有数值的比较操作符，同时也可以处理原子的否定。

原始的Neural LP框架不能直接支持有数值的事实：朴素的做法是将数值常量作为$\mathcal{C}$中的实体，但这将会非常难以处理，因为各自矩阵中非零的元素值非常非常多。类似地，朴素的处理否定原子的操作会引入操作不可行的稠密矩阵。

本文方法的主要思想是：隐式地表示必要的矩阵操作，可以使用动态规划、累积求和和排列（用于数值比较特征），也可以使用低秩分解（用于否定原子）。使用这一结构，我们可以形成相关的TensorLog操作符，并将其高效地集成到Neural LP框架中用于规则的抽取。

5.1 比较操作符

（1）Pair-wise Comparison

首先，隐式地表示和数值比较符相关的操作符。令$p,q\in (\mathbb{R}\cup \{NaN\}{)}^{|\mathcal{C}|}$表示两个特定特征的向量，其中$NaN$表示缺失值。比较操作符$M_{r_{pq}^{\le }}$定义为：

这一矩阵是针对KG上所有包含$p,q$的实体对的，因此$M_{r_{pq}^{\le }}$通常是稠密的，因此朴素的具体化将超过GPU内存的限制。而且，在现实中通常不需要明确地具体化TensorLog的关系矩阵。注意，在我们上面提到的Neural LP推理链中，所需要做的就是有效地计算关系矩阵和表示推理链中当前概率的某个向量之间的matrix-vector积。

---

考虑到特殊的情况：$p$和$q$都以升序进行排列，记为$\tilde{p},\tilde{q}$，相对应的比较矩阵记为${\tilde{M}}_{r_{pq}^{\le }}$。因为${\tilde{q}}_i\le {\tilde{q}}_{i+1},{\tilde{p}}_j\le {\tilde{p}}_{j+1}$，所以有如下的属性（P1）：

定义${\gamma }_i=argma{x}_j$使$({\tilde{M}}_{r_{pq}^{\le }}{)}_{ij}=1$，例如 ${\gamma }_i$是值为1的最后一个元素的索引。对于任意的向量$v$，我们可以使用这个$\gamma$向量计算需要的matrix-vector乘积：

$\gamma$值可以预先在CPU上进行计算，使用动态规划可以实现线性的复杂度，因为根据P1可知它的值是单调增的。另外，累积求和操作（cumsum）可以在$O(|C|)$内的时间内完成。

---

考虑一般的情况，也就是$p,q$没有进行排序：首先对输入的$v$进行排序，进行matrix-vector相乘操作，然后对结果重新排序为原始的顺序。令$P_p,P_q$分别表示$p,q$的转置矩阵（permutation matrices）。对应于比较操作符的matrix-vector乘积可写为：

（2）通过多原子符号匹配有效地使用数值比较

尽管上述的符号比较操作符为在Neural LP框架内实现这种比较，提供了一种有效的方法，但是也有明显的缺点。特别地，由于比较操作符是稠密的，当使用它去匹配图中的潜在实体时，就有可能生成大量的候选匹配。例如，操作符$(X.p\le Y.p)$将会连接有着最小的$p$值的实体和其他所有拥有属性$p$的实体，这将会降低找到正确目标的可能性。为使比较操作符更加有用，很自然地想到将其和其他的一些稀疏的操作符联合起来，例如：

如上所示的规则只会对$X$在图中的邻居进行搜索，同时遵循数值关系。令这两个并行的关系分别对应于操作符$M_{colleagueOf},M_{r_{pq}^{\le }}$。上述的合取操作可以通过如下的式子在TensorLog中执行：

其中$\odot$定义了element-wise乘积操作。不幸的是，上述的关系在标准的Neural LP框架中是不可学习的，因为Neural LP只支持matrix-vector操作的单个链$M_{q_n}...M_{q_2}{M}_{q_1}{v}_x$。然而，作者注意到，在乘法链中简单地缓存$v$的中间值是很简单的，并且用这种方式可以方便地计算Hadamard乘积。在KG的设置中，这正好对应了推理链中多处整合符号匹配的能力。

（3）分类操作符

作者也考虑到了更多的一般规则，在这种规则中，不一定非要对实体的两个数值属性间进行比较，也可以对这些属性的functions进行比较。

这种对于所有的实体进行这样的比较，可以很容易地通过TensorLog操作符得到，即给定数值$Z$相应的矩阵是一个对角矩阵。我们使用一个logistic模型对数值$Z$进行建模。即对于每个实体我们收集到特征向量$\varphi$，其中包含了从$\mathcal{N}$中得到的，和给定实体相关联的所有的数值（numerical values）。$M$对角线中的第$i$个元素可定义成$sigmoid(w^T\varphi +b)$，其中权重向量$w$和偏置向量$b$需要学习得到。在Neural LP框架中，可以使用反向传播很容易地学习到这些参数。

（4）否定操作符（Negated Operators）

对于一个关系$p\in \bar{\mathcal{R}}$，要想得到它的否定（negation），可以将对应的（稀疏）矩阵$M_p$中的所有0翻转为1以得到稠密的矩阵，但TensorLog不能直接支持这一操作。

为了计算出negated operator ${\bar{M}}_p\in \{0,1{\}}^{|\mathcal{C}|\times |\mathcal{C}|}$，我们使用了局部封闭世界的假设（local closed-world assumption）。对于给定的$M_p$，对那些要被翻转的元素进行了限制，即要被翻转的元素所在的行至少要有一个非零元素。negated operator ${\bar{M}}_p$的matrix-vector乘积可以写为：

其中$1_p\in \{0,1{\}}^{|\mathcal{C}|}$是$p$的indicator vector，当$p_i=NaN$时，使得$(1_p{)}_i=0$。$1$表示元素值全为1的向量。

等式（3）可以推广为比较操作符$M_{r_{pq}^{\circ }}$，即：

例如，${\bar{M}}_{r_{pq}^{\le }}v=1_p{1}_p^{T}v-M_{r_{pq}^{>}}v$。使用这种方式，我们就可以学习到规则体中有否定原子（negated atoms）的规则。

通过本文的方法学习到了规则后，作者和Yang等人[4]使用一样的过程，即将它们编码回等式（1）中的形式。

（5）Connection to Rules with Aggregates over Knowledge Graphs

使用上述方法抽取出来的规则属于带有外部计算的逻辑规则语言，并与知识表示中聚合的概念相关联。事实上，我们在这里展示的大部分公式都可以被看作是从知识图谱中获得聚合的学习规则的实例。这是当前研究的一个活跃领域，我们提出了使用(有限形式的)这样的聚合来学习规则的最初方法之一。

见附录A

6 实验

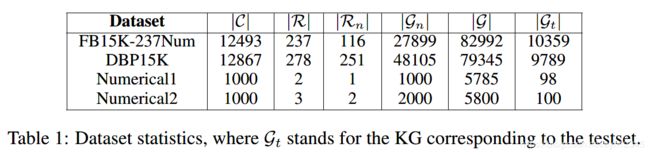
1、数据集

2、实验任务：链接预测

3、对比方法

本文的方法称为Neural-Num-LP，和以下两个baselines进行对比：

• AnyBURL：用于学习Horn规则的自底向上的方法（Horn规则：例如只有positive atoms没有比较操作符的规则）；
• Neural-LP：可微的规则学习系统。

4、实验结果

本文的方法和baselines对比的实验结果：

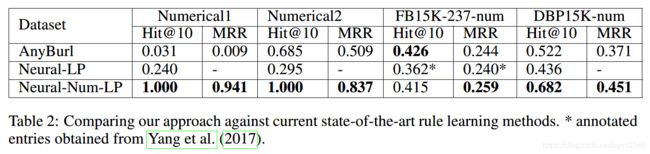
实验结果可以看出，本文基于Neural-LP拓展出的方法Neural-Num-LP在自造的数据集上，达到了一种很好的效果，而另外俩个相关的baseline因为没有加入数值推理的逻辑，所以效果不行；同时，在俩个标准知识图谱上，Neural-Num-LP也能达到一个较好的效果，体现出框架的一方面很好的保存了关系推理的功能，又较好的建模了数值推理的逻辑。

图 3展示了本文的方法抽取出来的一个规则例子。规则$r^1,r^2$分别从Numerical1和Numerical2数据集中抽取出来，规则$r^3$来自FB15K-237-num数据集，其他的规则来自于DBPedial15K数据集。

其中函数$f$是自变量数值属性的线性组合。

7 总结

本文解决的任务是从大型的KG中学习数值型的规则。

特别地，作者考虑到了在规则体中，允许使用数值比较操作符和聚合（例如 外部oracle查询）来聚合实体的数值属性。

Neural-LP方法是基于TensorLog的最近流行的方法，但是它不支持数值型的规则，因为会导致稠密的矩阵操作。本文提出了Neural-LP框架的扩展，允许通过高效地表示比较和分类操作符、否定和多原子符号匹配从KG中学习这些规则。

未来的工作：对本文的模型进行进一步的扩展，允许更一般的规则，包括复杂的外部计算，以及在规则头有存在变量的规则。

---

以下转自[6]：ICLR 2020|知识图谱推理框架：基于向量空间的推理和数值逻辑推理

先前的基于Neural-LP（Neural Logic Programming）框架的模型一般只能在由<实体，关系，实体>组成的知识图谱结构谓词上进行推理，而不能解决涉及到实体属性数值方面的问题，例如“比A年长的人是谁？”本文是在Neural-LP框架上进行了拓展，加入了数值推理的逻辑，解决了数值比较，属性聚合以及求反等三个方面的推理。

具体来说，文中把实体属性的数值比较也定义了成了一种谓词操作：

其中，p, q表示待比较的属性，这样就可以自然的将属性谓词使用类似于Neural-LP的谓词矩阵运算来实现。但是与关系谓词不同，属性谓词矩阵通常是稠密的，因为属性在实体上较为通用，而稠密矩阵的相乘复杂度特别高，所以文中定义了一种排序正则化的思路，将矩阵相乘转化为排序后的累加，极大地降低了复杂度。有了之前的定义，求反操作就比较容易得出，即对于之前得到的属性谓词矩阵的每一维取非(0->1, 1->0)，但会遵循Local Closed-world Assumption(LCWA)，即至少有一个非0值的行才会取非。

基于定义的数值比较和求反操作，通过在之上施加聚合函数 F 去达到多个属性操作聚合作用的效果，例如下面一条逻辑表达式：

其中 F 代表的聚合操作就是由俩种基础的属性比较操作的某种联合作用，聚合函数可用任意的神经网络来替换，文中使用了简单的MLP。

参考文献

[1] Fan Yang, Zhilin Yang, and William W. Cohen. Differentiable learning of logical rules for knowledge base reasoning. In NeurIPS, pp. 2316–2325, 2017.

[2] Christian Meilicke, Melisachew Wudage Chekol, Daniel Ruffinelli, and Heiner Stuckenschmidt. Anytime bottom-up rule learning for knowledge graph completion. In Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence, IJCAI 2019, Macao, China, August 10-16, 2019, pp. 3137–3143, 2019.

[3] Stefano Ortona, Venkata Vamsikrishna Meduri, and Paolo Papotti. Rudik: Rule discovery in knowledge bases. PVLDB, 11(12):1946–1949, 2018b.

[4] Fan Yang, Zhilin Yang, and William W. Cohen. Differentiable learning of logical rules for knowledge base reasoning. In NeurIPS, pp. 2316–2325, 2017.

[5] Alberto Garc´a-Dur´an and Mathias Niepert. Kblrn: End-to-end learning of knowledge base representations with latent, relational, and numerical features. In UAI, pp. 372–381, 2018.

[6] ICLR 2020|知识图谱推理框架：基于向量空间的推理和数值逻辑推理 https://www.bilibili.com/read/cv5893715/