leetcode---动态规划(3)
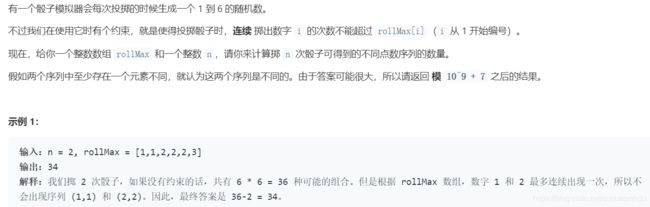
377. 组合总和 Ⅳ
class Solution {
public int combinationSum4(int[] nums, int target) {
int[] dp = new int[target+1];
Arrays.fill(dp, -1);
return f(nums, target, dp);
}
private int f(int[] nums, int target, int[] dp){
if(target < 0){
return 0;
}
if(dp[target] != -1){
return dp[target];
}
if(target == 0){
return dp[target] = 1;
}
int ans = 0;
for(int i = 0; i < nums.length; i++){
ans += f(nums, target-nums[i], dp);
}
return dp[target] = ans;
}
}
1223. 掷骰子模拟
class Solution {
private int mod = 1000000007;
public int dieSimulator(int n, int[] rollMax) {
int[][][] dp = new int[n+1][7][16]; // 抛k次,数字i最后连续出现j次,的结果
for(int k = 1; k < 7; k++){
dp[1][k][1] = 1;
}
for(int k = 2; k <= n; k++){
for(int i = 1; i <= 6; i++){
for(int j = 1; j <= rollMax[i-1]; j++){
if(j > 1){
dp[k][i][j] = dp[k-1][i][j-1] % mod;
}else{
for(int p = 1; p <= 6; p++){
if(p == i){
continue;
}
for(int cnt = 1; cnt <= rollMax[p-1]; cnt++){
dp[k][i][j] = (dp[k][i][j] % mod + dp[k-1][p][cnt] % mod) % mod;
}
}
}
}
}
}
int res = 0;
for(int i = 1; i <= 6; i++){
for(int j = 1; j <= rollMax[i-1]; j++){
res = (res % mod + dp[n][i][j] % mod) % mod;
}
}
return res;
}
// 下面回溯法是错的,题目说的是不能【连续】出现,不是出现次数。。。
// 调用下面函数之前对rollMax数组进行处理,凡是大于等于n的都搞成n
// private int f(int[] a, int n){
// if(n == 0){
// return 1;
// }
// int ans = 0;
// for(int i = 0; i < a.length; i++){
// if(a[i] >= 1){
// a[i] -= 1;
// ans += f(a, n-1);
// a[i] += 1;
// }
// }
// return ans;
// }
}
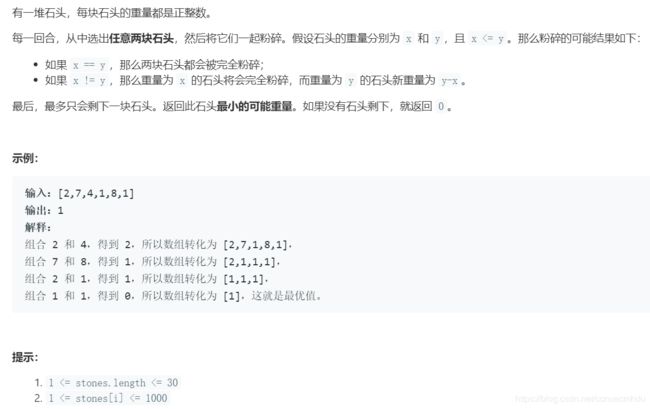
1049. 最后一块石头的重量 II
class Solution {
// 题目据说是转化成不断加减最终得到的最小值。。。
// 笔者无法给出细致证明,但是考虑一下确实是的。。。
public int lastStoneWeightII(int[] stones) {
Map<String, Integer> dp = new HashMap<>();
return f(stones, 0, 0, dp);
}
private int f(int[] stones, int i, int sum, Map<String, Integer> dp){
if(i == stones.length){
dp.put(""+i+"_"+sum, sum);
return sum;
}
if(dp.containsKey(i+"_"+sum)){
return dp.get(i+"_"+sum);
}
int res = Math.min(Math.abs(f(stones, i+1, sum-stones[i], dp)),
Math.abs(f(stones, i+1, sum+stones[i], dp)));
dp.put(i+"_"+sum, res);
return res;
}
}
467. 环绕字符串中唯一的子字符串
class Solution {
public int findSubstringInWraproundString(String p) {
// 本题转化成求以a~z结尾的最长子串长度之和,注意s是循环的。。
// 如zab,结果是1+2+3=6
int[] dp = new int[26];
char[] cs = p.toCharArray();
int last = 1; // 一直连续就加 ,否则从1开始
for(int i = 0; i < cs.length; i++){
dp[cs[i]-'a'] = dp[cs[i]-'a'] > 1 ? dp[cs[i]-'a'] : 1;
if(i > 0 && (cs[i]-cs[i-1]==1 || cs[i-1]-cs[i]==25)){
last += 1;
dp[cs[i]-'a'] = dp[cs[i]-'a'] < last ? last : dp[cs[i]-'a'];
}else{
last = 1;
}
}
int res = 0;
for(int i = 0; i < 26; i++){
res += dp[i];
}
return res;
}
}
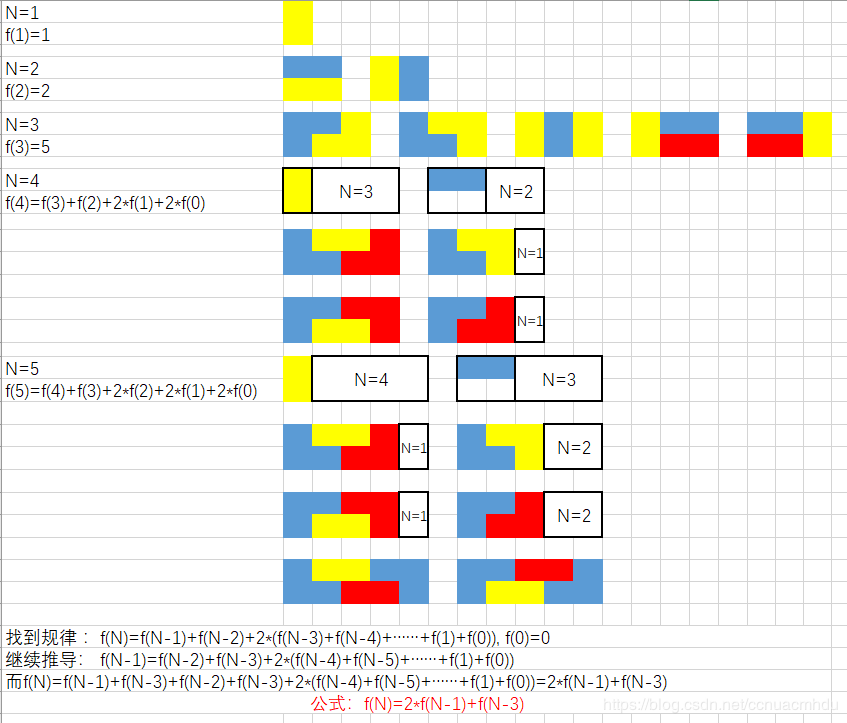
790. 多米诺和托米诺平铺
class Solution {
private int mod = 1000000007;
public int numTilings(int N) {
int[] dp = new int[N+3];
dp[0] = 1;
dp[1] = 1;
dp[2] = 2;
dp[3] = 5;
for(int i = 4; i <= N; i++){
dp[i] = (2*(dp[i-1] % mod) % mod + dp[i-3] % mod) % mod;
}
return dp[N] % mod;
}
}
152. 乘积最大子序列
class Solution {
// 暴力枚举以nums[i]结束的最优解
public int maxProduct(int[] nums) {
int ans = Integer.MIN_VALUE;
for(int i = 0; i < nums.length; i++){
int product = 1;
int tmp = nums[i];
for(int j = i; j >= 0; j--){
product *= nums[j];
tmp = Math.max(product, tmp);
ans = Math.max(ans, tmp);
}
}
return ans;
}
}
【代码二】错误—动态规划
// [-2,3,-4],以nums[i]结尾的最优解,状态转移是错的。。
class Solution {
public int maxProduct(int[] nums) {
int[] dp = new int[nums.length];
dp[0] = nums[0];
int ans = dp[0];
for(int i = 1; i < nums.length; i++){
dp[i] = dp[i-1]*nums[i] <= nums[i] ? nums[i] : dp[i-1]*nums[i];
ans = Math.max(ans, dp[i]);
}
return ans;
}
}
【代码三】通过—动态规划
class Solution {
// 2,3,-2,4
// max: 2,6,-2,4
// min: 2,3,-12,-48
public int maxProduct(int[] nums) {
int[] dpMin = new int[nums.length]; // 以nums[i]结尾的连续子数组的最大值
int[] dpMax = new int[nums.length]; // 以nums[i]结尾的连续子数组的最小值
dpMin[0] = dpMax[0] = nums[0];
int ans = dpMax[0];
for(int i = 1; i < nums.length; i++){
if(nums[i] < 0){
dpMax[i] = Math.max(dpMin[i-1]*nums[i], nums[i]);
dpMin[i] = Math.min(dpMax[i-1]*nums[i], nums[i]);
}else{
dpMax[i] = Math.max(dpMax[i-1]*nums[i], nums[i]);
dpMin[i] = Math.min(dpMin[i-1]*nums[i], nums[i]);
}
ans = Math.max(ans, dpMax[i]);
}
return ans;
}
}
5. 最长回文子串
class Solution {
// 转化成最长公共子串
// "aacdefcaa" -> 不该返回aac,而该返回aa
public String longestPalindrome(String s) {
if(s.length() == 0){
return "";
}
if(s.length() == 1){
return s.charAt(0) + "";
}
String s2 = new String(new StringBuilder(s).reverse());
// 求最长公共子串
int[][] dp = new int[s.length()][s.length()];
int ans = 0;
int x = 0;
int y = 0;
for(int i = 0; i < s.length(); i++){
dp[0][i] = s.charAt(0) == s2.charAt(i) ? 1 : 0;
dp[i][0] = s.charAt(i) == s2.charAt(0) ? 1 : 0;
}
for(int i = 1; i < s.length(); i++){
for(int j = 1; j < s2.length(); j++){
dp[i][j] = (s.charAt(i) == s2.charAt(j)) ? dp[i-1][j-1] + 1 : 0;
if(ans < dp[i][j]
&& i-dp[i][j]+1 == s.length()-1-j
&& i == s.length()-1-(j-dp[i][j]+1)){
ans = dp[i][j];
x = i;
y = j;
}
}
}
int tmpX = x;
int tmpY = y;
while(x-- > 0 && y-- > 0 && s.charAt(x) == s2.charAt(y)){}
return s.substring(x+1, tmpX+1);
}
}
下面红色的两个aa才是匹配的。。逆序后的字符串再逆着打上下标,下图此时,j=i-1,i=j+1。结合图可理解i-dp[i][j]+1 == s.length()-1-j && i == s.length()-1-(j-dp[i][j]+1)

【代码二】通过
class Solution {
// 回文串本身长度可为奇偶,所以回文串中心可能是某个元素,也有可能是两个元素之间的空隙
// a b b a
// a b a
public String longestPalindrome(String s) {
if(s == null || s.length() == 0){
return "";
}
int L = 0;
int R = 0;
for(int i = 0; i < s.length(); i++){
int len1 = f(s, i, i); // 奇
int len2 = f(s, i, i+1); // 偶
int len = (len1 > len2) ? len1 : len2;
// 下面是合并了奇偶两种情况
if(len > R-L+1){
L = i - (len-1)/2;
R = i + len/2;
}
}
return s.substring(L, R+1);
}
private int f(String s, int L, int R){
while(L >= 0 && R < s.length() && s.charAt(L) == s.charAt(R)){
L--;
R++;
}
return R-L-1; // (R-1)-(L+1)+1
}
}
368. 最大整除子集
class Solution {
// 排序后,i
// 转化成最长上升子序列。。dp[i]表示以nums[i]结尾的最长上升子序列长度。
// dp[i] = Math.max(1, dp[k]+1)
public List<Integer> largestDivisibleSubset(int[] nums) {
if(nums.length == 0){
return new ArrayList<>();
}
if(nums.length == 1){
return Arrays.asList(nums[0]);
}
Arrays.sort(nums);
int[] dp = new int[nums.length];
dp[0] = 1;
int ans = dp[0];
int pos = 0;
int[] path = new int[nums.length];
Arrays.fill(path, -1);
for(int i = 1; i < nums.length; i++){
dp[i] = 1;
for(int j = 0; j < i; j++){
if(nums[i] % nums[j] == 0 && dp[i] < dp[j] + 1){
dp[i] = dp[j] + 1;
path[i] = j; // 之所以可以这么记录,主因是i的前任一旦定了,后续根本就不会变了
}
}
if(ans < dp[i]){
ans = dp[i];
pos = i; // 递推过程中,记录最大的dp对于的位置下标
}
}
List<Integer> resList = new ArrayList<>();
while(pos != -1){
resList.add(0, nums[pos]);
pos = path[pos];
}
return resList;
}
}
375. 猜数字大小 II
class Solution {
public int getMoneyAmount(int n) {
int[][] dp = new int[n+2][n+2];
for(int i = 0; i <= n; i++){
Arrays.fill(dp[i], -1);
}
return f(1, n, dp);
}
// [L, R]中选一个直到最后猜出所耗费的在保证能赢游戏的前提下的至少的钱
private int f(int L, int R, int[][] dp){
if(L >= R){ // 这里有可能L=n+1,dp开n+2
return dp[L][R] = 0;
}
if(dp[L][R] != -1){
return dp[L][R];
}
int ans = Integer.MAX_VALUE;
for(int i = L; i <= R; i++){
// 为确保必赢游戏,下面用到了max
ans = Math.min(ans, i + Math.max(f(L, i-1, dp), f(i+1, R, dp)));
}
return dp[L][R] = ans;
}
}
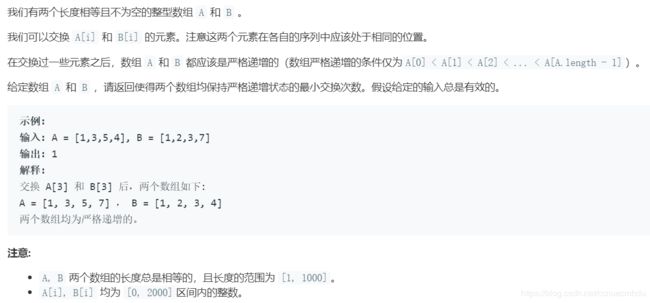
801. 使序列递增的最小交换次数
class Solution {
// 1.暴力想法。先找出导致不严格递增的点,交换必发生在这些点上,然后尝试
// 交换任意一个点,检查整个数组是否严格递增,若是返回1,否则,尝试交换
// 任意两个点,检查整个数组是否严格递增,若是返回2,否则,继续尝试。。。
// (时间复杂度太大。。)
// 2.暴力想法。每个位置要么交换要么不交换,全都搞一遍。。
// 3.注意到导致不严格递增的点,可以交换这两个点,也可以交换该点前面的那一对点。
// 最终的最少交换次数应该就是这两种方式中的较小值。(解释:若到i位置不严格递增了,那么
// 对于i-1和i位置,若都不交换维持原状,不能恢复严格递增;若两位置都交换,也不
// 能恢复严格递增,那么必定要交换一处)。
// 4.【最终必有(A[i]>A[i-1] && B[i]>B[i-1]) 或 (A[i]>B[i-1] && B[i]>A[i-1])成立】
// 利用这句话写代码。。。对于某位置来说要么换,要么不换。。。
public int minSwap(int[] A, int[] B) {
int n = A.length;
int[] change = new int[n]; // 本次交换,到本次的最小交换次数
int[] notChange = new int[n]; // 本次不交换,到本次的最小交换次数
change[0] = 1;
notChange[0] = 0;
for(int i = 1; i < n; i++){
// 两种情况都成立,可换可不换,随意
if((A[i] > A[i-1] && B[i] > B[i-1]) && (A[i] > B[i-1] && B[i] > A[i-1])){
notChange[i] = Math.min(change[i-1], notChange[i-1]);
change[i] = Math.min(change[i-1], notChange[i-1]) + 1;
}
// 只满足第一种情况,i和i-1位置要么都换,要么都不换
if((A[i] > A[i-1] && B[i] > B[i-1]) && !(A[i] > B[i-1] && B[i] > A[i-1])){
notChange[i] = notChange[i-1];
change[i] = change[i-1] + 1;
}
// 只满足第二种情况,i和i-1位置必须换其一
if(!(A[i] > A[i-1] && B[i] > B[i-1]) && (A[i] > B[i-1] && B[i] > A[i-1])){
notChange[i] = change[i-1];
change[i] = notChange[i-1] + 1;
}
}
return Math.min(change[n-1], notChange[n-1]);
}
}
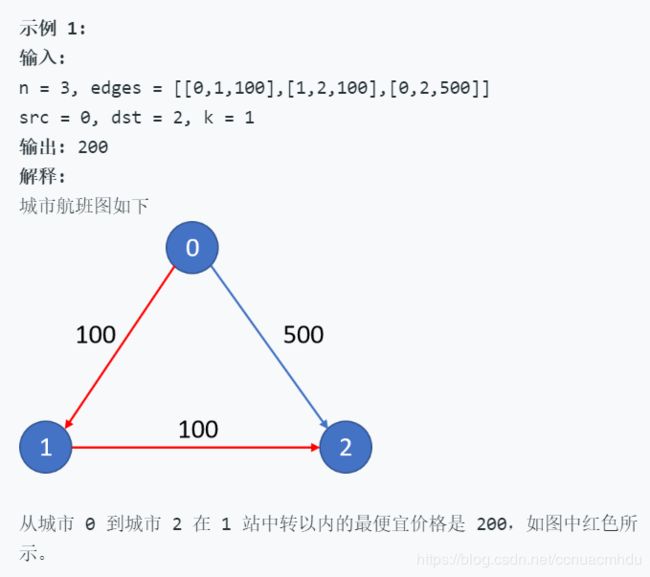
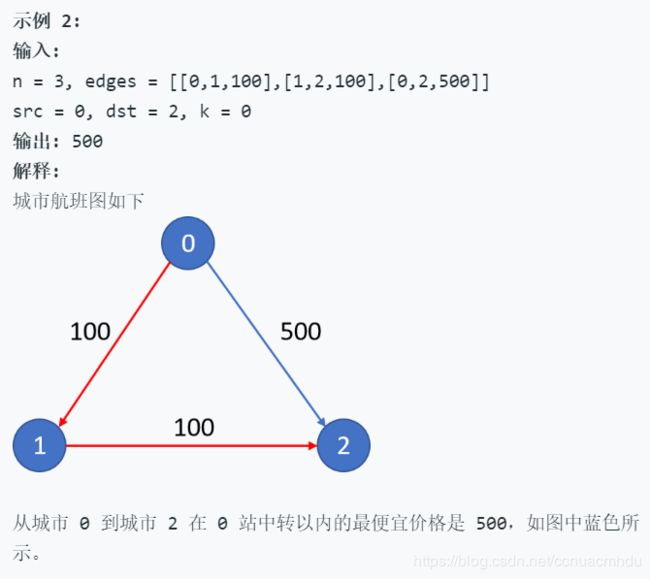
787. K 站中转内最便宜的航班
1218. 最长定差子序列
class Solution {
// 1.暴力(超时)
// 2.DP(超时)。以i结尾的最长等差自序列长度是dp[i]
// dp[i] = max(dp[i], dp[j]), arr[i] - arr[j] == difference
// 3.DP(通过)。以arr[i]结尾的最长等差自序列长度是dp[arr[i]]
// dp[arr[i]] = max(dp[arr[i]], dp[arr[i]-difference] + 1) // i-difference有可能为负,可用map记录
public int longestSubsequence(int[] arr, int difference) {
int[] dp = new int[arr.length];
int res = 1;
Map<Integer, Integer> map = new HashMap<>();
for(int i = 0; i < arr.length; i++){
if(map.containsKey(arr[i]-difference)){
dp[i] = map.get(arr[i]-difference) + 1;
}else{
dp[i] = 1;
}
map.put(arr[i], dp[i]);
res = Math.max(res, dp[i]);
}
return res;
}
}
464. 我能赢吗
class Solution {
public boolean canIWin(int maxChoosableInteger, int desiredTotal) {
if(desiredTotal <= 0){ // 刚开始就达到了,我方(先手)赢
return true;
}
if((maxChoosableInteger+1)*maxChoosableInteger/2 < desiredTotal){ // 永远达不到,我方败
return false;
}
char[] vis = new char[maxChoosableInteger+1];
Arrays.fill(vis, '0');
Map<String, Boolean> map = new HashMap<>();
return f(desiredTotal, vis, map);
}
// 回溯法+记忆化
private boolean f(int desired, char[] vis, Map<String, Boolean> map){
if(desired <= 0){ // 我方不可选,我方败。。
return false;
}
String key = new String(vis);
if(map.containsKey(key)){
return map.get(key);
}
boolean ans = false;
// 我方随机选一个,看对方成败
for(int i = 1; i < vis.length; i++){
if(vis[i] == '0'){
vis[i] = '1'; // 选择i
ans = !f(desired-i, vis, map); // 对手的反
vis[i] = '0'; // 回溯,每次搞完后,恢复原状,供下一轮搞
if(ans == true){
break;
}
}
}
map.put(new String(vis), ans);
return ans;
}
}
673. 最长递增子序列的个数
class Solution {
// 以nums[i]结束的最长递增自序列长度dp[i]
// dp[i] = max(dp[i], dp[j] + 1), nums[i] > nums[j], i>=j
public int findNumberOfLIS(int[] nums) {
int[] dp = new int[nums.length];
Arrays.fill(dp, 1);
int maxLen = 1;
for(int i = 1; i < nums.length; i++){
for(int j = i-1; j >= 0; j--){
if(nums[i] > nums[j]){
dp[i] = Math.max(dp[i], dp[j]+1);
}
}
maxLen = Math.max(maxLen, dp[i]);
}
List<Integer> indexes = new ArrayList<>();
for(int i = 0; i < nums.length; i++){
if(dp[i] == maxLen){
indexes.add(i);
}
}
List<List<Integer>> G = new ArrayList<>(); // 建立图
for(int i = 0; i < nums.length; i++){
G.add(new ArrayList<>());
}
for(int i = 0; i < nums.length; i++){ // 建立图,邻接表
for(int j = i-1; j >= 0; j--){
if(nums[i] > nums[j] && dp[i] == dp[j]+1){
G.get(i).add(j);
}
}
}
int ans = 0;
for(int i = 0; i < indexes.size(); i++){
ans += dfs(G, indexes.get(i), maxLen);
}
return ans;
}
private int dfs(List<List<Integer>> G, int i, int len){
if(len == 1){
return 1;
}
int ans = 0;
for(int k = 0; k < G.get(i).size(); k++){
ans += dfs(G, G.get(i).get(k), len-1);
}
return ans;
}
}
1186. 删除一次得到子数组最大和
898. 子数组按位或操作
class Solution {
// 想暴力搞定,但一看数据10^5,O(N^2)会超时。。
// 参考题解(https://leetcode-cn.com/u/wdw87/)
// dp[i][j]表示以arr[i]结尾的删除j次的最大和,j<=i+1
// dp[i][j] = max(dp[i-1][j]+arr[i], dp[i-1][j-1])
public int maximumSum(int[] arr) {
int k = 1; // 删除k次
int[][] dp = new int[arr.length][k+1];
dp[0][0] = arr[0];
int max = dp[0][0];
for(int i = 1; i < arr.length; i++){
dp[i][0] = dp[i-1][0] <= 0 ? arr[i] : dp[i-1][0] + arr[i];
max = Math.max(max, dp[i][0]);
}
for(int i = 1; i < arr.length; i++){
for(int j = 1; j <= k; j++){
dp[i][j] = Math.max(dp[i-1][j]+arr[i], dp[i-1][j-1]);
max = Math.max(dp[i][j], max);
}
}
return max;
}
}
【代码一】通过—暴力(对暴力优化)
class Solution {
// 参考官方题解
// 根据后面附注的暴力法优化。暴力过程中,比如以i结尾的数不断向前进行或运算,
// 在或运算过程中,都是在A[i]的基础上变化,都是对A[i]的某些位进行改变。。
// 每次有可能增加几个二进制位1,最多增加到32个都是1为止。。。也就是说,如果
// 每次只增加一个1二进制位,最多进行32次都变成1就不会再变了。。也就是说,最
// 多只会导致有32个数。。。然后拿着这些数再和A[i+1]进行或运算。。往后推进。。
public int subarrayBitwiseORs(int[] A) {
Set<Integer> cur = new HashSet<>();
Set<Integer> ans = new HashSet<>();
for(int i = 0; i < A.length; i++){
Set<Integer> next = new HashSet<>();
next.add(A[i]);
for(Integer x : cur){
next.add(x | A[i]);
}
ans.addAll(next);
cur = next;
}
return ans.size();
}
// 暴力法(超时)。暴力可以根据以某数结束来分类,也可以根据在某区间段内分类。
// public int subarrayBitwiseORs(int[] A) {
// Set set = new HashSet<>();
// for(int i = 0; i < A.length; i++){
// int res = A[i];
// set.add(res);
// for(int j = i-1; j >= 0; j--){
// res |= A[j];
// set.add(res);
// }
// }
// return set.size();
// }
}
837. 新21点
class Solution {
// 根据暴力法可得:
// dp[i] = 1/W(dp[i+1] + dp[i+2] + …… + dp[i+W])
public double new21Game(int N, int K, int W) {
if(K == 0){
return 1.0;
}
double[] dp = new double[20000];
for(int cur = K; cur <= N; cur++){
dp[cur] = 1.0;
}
for(int cur = N+1; cur >= K && cur <= K-1+W; cur++){
dp[cur] = 0.0;
}
int pos = K-1+W-W;
double sum = 0.0;
for(int j = 1; j <= W; j++){
sum += 1.0/W*dp[pos+j];
}
dp[pos] = sum;
for(int i = pos-1; i >= 0; i--){
// 这就是关键优化所在。。相当于滑动窗口的思想,避免每次都重复计算i+1,……,i+W
dp[i] = 1.0/W*dp[i+1] + dp[i+1] - 1.0/W*dp[i+1+W];
}
return dp[0];
}
// // 记忆化搜索(超时),这道题说明记忆化搜索缺陷,不方便继续优化。。
// public double new21Game(int N, int K, int W) {
// double[] dp = new double[20000];
// Arrays.fill(dp, -1.0);
// return f(N, K, W, 0, dp);
// }
// private double f(int N, int K, int W, int cur, double[] dp){
// if(dp[cur] >= 0.0){
// return dp[cur];
// }
// if(cur >= K){
// return cur <= N ? 1 : 0;
// }
// double ans = 0.0;
// for(int i = 1; i <= W; i++){
// double res = f(N, K, W, cur+i, dp);
// if(res > 0.0){
// ans += 1.0/W*res;
// }
// }
// return dp[cur] = ans;
// }
}
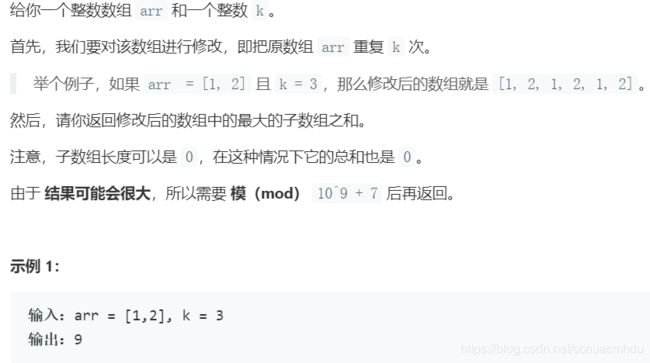
1191. K 次串联后最大子数组之和
class Solution {
private int mod = 1000000007;
// 都说了,变成原来的2倍的就能搞定了。。只需要求一下2倍的最大和以及所有数之和就OK
public int kConcatenationMaxSum(int[] arr, int k) {
if(k == 1){
return f(arr) % mod;
}
int[] a = new int[arr.length * 2];
long sum = 0;
for(int i = 0; i < arr.length; i++){
a[i] = arr[i];
a[i+arr.length] = arr[i];
sum += a[i];
}
return (int)(f(a) + (k-2)*Math.max(sum, 0) % mod);
}
// 常规DP,求子数组最大和
private int f(int[] arr){
int cur = 0;
int ans = 0;
for(int i = 0; i < arr.length; i++){
cur = cur <= 0 ? arr[i] : cur + arr[i];
ans = ans < cur ? cur : ans;
}
return ans;
}
}
523. 连续的子数组和
class Solution {
public boolean checkSubarraySum(int[] nums, int k) {
// 暴力(辅助数组优化)
int[] help = new int[nums.length];
help[0] = nums[0];
for(int i = 1; i < nums.length; i++){
help[i] = help[i-1] + nums[i];
}
for(int i = 0; i < nums.length; i++){
for(int j = i+1; j < nums.length; j++){
int sum = help[j] - help[i] + nums[i];
if((sum==0 && k==0) || (k!=0 && sum%k==0)){
return true;
}
}
}
return false;
}
}
特别说明
本文参考leetcode官方网站题库及相关讨论区解答。链接地址