【笔记3-2】CS224N课程笔记+作业参考代码 - 词向量表示 word2vec
CS224N(二)Word Vectors
- 如何表示字的含义
- 基于SVD的方法
- 基于迭代的方法 - Word2vec
- CBOW (continuous bag of words)
- skip-gram
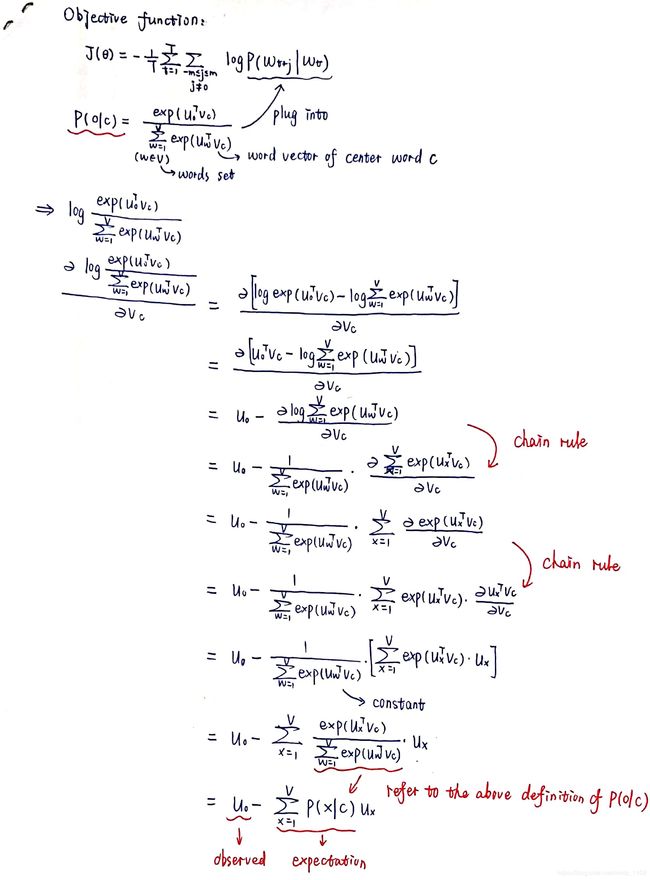
- 梯度的推导过程
- skip-gram和CBOW的改进
- Assignment 1 参考代码
【笔记3-1】CS224N课程笔记 - 深度自然语言处理
【笔记3-3】CS224N课程笔记 - 高级词向量表示
【笔记3-4】CS224N课程笔记 - 分类与神经网络
【笔记3-5】CS224N课程笔记 - 依存分析
【笔记3-6】CS224N课程笔记 - RNN和语言模型
【笔记3-7】CS224N课程笔记 - 神经机器翻译seq2seq注意力机制
【笔记3-8】CS224N课程笔记 - 卷积神经网络
CS224n:深度学习的自然语言处理(2017年冬季)1080p https://www.bilibili.com/video/av28030942/
涉及到的论文:
Efficient Estimation of Word Representations in Vector Space (2013,Tomas Mikolov, Kai Chen, Greg Corrado, Jeffrey Dean)
https://arxiv.org/pdf/1301.3781.pdf
Distributed Representations of Words and Phrases and their Compositionality (2013, Tomas Mikolov, Ilya Sutskever, Kai Chen, Greg Corrado, Jeffrey Dean)
https://arxiv.org/pdf/1310.4546.pdf
关键词:词向量,SVD,skip-gram,CBOW,负采样,word2vec,hierarchical softmax
如何表示字的含义
meaning=denotation:
signifier (symbol) ⇔ \Leftrightarrow ⇔ signified (idea or thing)
Usable meaning in computer:
以往会使用WordNet来查找同义词以及重名词
WorldNet的缺点:
- 缺乏字词之间的细微差别
- 丢失字词的新含义
- 带有主观色彩
- 需要大量的人力劳动进行标注
- 难以准确计算字词之间的相似性
出发点:字典里面有许多不同的单词,如果要对字典里的N个单词进行表示,需要将其映射到一个N维的空间,但是,实际上很多单词之间存在关联,由此出发,必定存在一个K维的空间,K< 字词的离散型符号表示: 缺点: 所有向量之间都是正交的,无法获取词语之间的相似性。 用上下文来表示单词: 构建词向量的方法: (word embedding/representation) 对于SVD构造的词向量,先对整个数据集进行遍历,并统计所有单词的共现现象,来生成一个矩阵X。然后对这个矩阵进行奇异值分解,即 X = U S V T X = USV^T X=USVT,然后取矩阵U的行向量作为整个字典中单词的词向量表示。 矩阵X的构造方法: 上述方法能够给我们提供单词的语义和词性信息,但是这个方法依旧存在一定的问题: 因此提出基于迭代的方法-word2vec来解决上述问题。 与上述需要遍历整个文档库的SVD方法不同,word2vec的方法每次迭代都会对单词基于上下文的概率进行更新。 大致思想:设计一个模型,用模型的参数来作为单词的向量表示,然后对模型进行训练,在每次迭代中根据loss对参数进行更新,最终得到的更新过后的参数就是单词的向量表示。 word2vec当中包含两种算法:CBOW(根据上下文词汇的词向量来预测中心词)skip-gram(根据中心词来预测上下文单词的概率分布) CBOW是根据上下文预测或生成中心词的方法。 了解CBOW的算法之后,就是对矩阵U和V的构造过程,需要根据目标损失函数使用梯度下降的方法求解。 根据信息论当中对两个分布的距离的计算方法,使用交叉熵来计算损失函数: H ( y ^ , y ) = − ∑ j = 1 ∣ V ∣ y j l o g ( y ^ j ) = − y i l o g ( y ^ i ) H(\hat{y},y)=-\sum_{j=1}^{|V|}y_jlog(\hat{y}_j)=-y_ilog(\hat{y}_i) H(y^,y)=−j=1∑∣V∣yjlog(y^j)=−yilog(y^i)因此优化目标为: m i n J = − l o g P ( w c ∣ w c − m , . . . , w c − 1 , w c + 1 , . . . , w c + m ) = − l o g P ( u c ∣ v ^ ) = − l o g e x p ( u c T v ^ ) ∑ j = 1 ∣ V ∣ e x p ( u j T v ^ ) = − u c T v ^ + l o g ∑ j = 1 ∣ V ∣ e x p ( u j T v ^ ) min J = -logP(w_c|w_{c-m},...,w_{c-1},w_{c+1},...,w_{c+m})\\ =-logP(u_c|\hat{v})=-log\frac{exp(u_c^T\hat{v})}{\sum_{j=1}^{|V|}exp(u_j^T\hat{v})}\\ =-u_c^T\hat{v}+log\sum_{j=1}^{|V|}exp(u_j^T\hat{v}) minJ=−logP(wc∣wc−m,...,wc−1,wc+1,...,wc+m)=−logP(uc∣v^)=−log∑j=1∣V∣exp(ujTv^)exp(ucTv^)=−ucTv^+logj=1∑∣V∣exp(ujTv^)优化的过程中使用SGD对参数进行更新。 思想与CBOW类似,但是这里是利用中心词来对上下文单词出现的概率进行预测。 同样的,定义目标函数: m i n J = − l o g P ( w c − m , . . . , w c − 1 , w c + 1 , . . . , w c + m ∣ w c ) = − l o g ∏ j = 0. j ≠ m 2 m P ( w c − m + j ∣ w c ) = − l o g ∏ j = 0 , j ≠ m 2 m P ( u c − m + j ∣ v c ) = − l o g ∏ j = 0 , j ≠ m 2 m e x p ( u c − m + j T v c ) ∑ k = 1 ∣ V ∣ e x p ( u k T v c ) = − ∑ j = 0 , j ≠ m 2 m u c − m + j T v c + 2 m l o g ∑ k = 1 ∣ V ∣ e x p ( u k T v c ) minJ=-logP(w_{c-m},...,w_{c-1},w_{c+1},...,w_{c+m}|w_c)\\=-log\prod_{j=0.j\neq m}^{2m}P(w_{c-m+j}|w_c)\\=-log\prod_{j=0,j\neq m}^{2m}P(u_{c-m+j}|v_c)\\=-log\prod_{j=0,j\neq m}^{2m}\frac{exp(u_{c-m+j}^Tv_c)}{\sum_{k=1}^{|V|}exp(u_k^Tv_c)}\\=-\sum_{j=0,j\neq m}^{2m}u_{c-m+j}^Tv_c+2mlog\sum_{k=1}^{|V|}exp(u_k^Tv_c) minJ=−logP(wc−m,...,wc−1,wc+1,...,wc+m∣wc)=−logj=0.j̸=m∏2mP(wc−m+j∣wc)=−logj=0,j̸=m∏2mP(uc−m+j∣vc)=−logj=0,j̸=m∏2m∑k=1∣V∣exp(ukTvc)exp(uc−m+jTvc)=−j=0,j̸=m∑2muc−m+jTvc+2mlogk=1∑∣V∣exp(ukTvc)同样的,对于这个目标函数,也可以使用SGD来进行优化和参数更新。 skip-gram示例: 注意: 最小化目标函数 ⇔ \Leftrightarrow ⇔ 最大化预测准确率 为什么要用到两个向量? 提高训练效率的方法: 负采样 在前文中,对单词预测时计算的概率是一个softmax函数(max: 表示放大最大值的概率; soft: 表示对较小的值依旧分配一定的概率)在计算的过程中,分母包含对所有点乘的加和,每一次迭代都需要对分母进行一次计算,这样会导致巨大的计算量,因此需要找到更加高效的训练方法——负采样,negative sampling 使用负采样的方法对loss进行近似,此时参数的求解就变成了对下述问题的求解: θ = a r g m a x θ ∏ ( w , c ) ∈ D P ( D = 1 ∣ w , c , θ ) ∏ ( w , c ) ∈ D ~ P ( D = 0 ∣ w , c , θ ) = a r g m a x θ ∏ ( w , c ) ∈ D P ( D = 1 ∣ w , c , θ ) ∏ ( w , c ) ∈ D ~ ( 1 − P ( D = 1 ∣ w , c , θ ) ) = a r g m a x θ ∑ ( w , c ) ∈ D l o g P ( D = 1 ∣ w , c , θ ) + ∑ ( w , c ) ∈ D ~ l o g ( 1 − P ( D = 1 ∣ w , c , θ ) ) = a r g m a x θ ∑ ( w , c ) ∈ D l o g 1 1 + e x p ( − u w T v c ) + ∑ ( w , c ) ∈ D ~ l o g ( 1 − 1 1 + e x p ( − u w T v c ) ) = a r g m a x θ ∑ ( w , c ) ∈ D l o g 1 1 + e x p ( − u w T v c ) + ∑ ( w , c ) ∈ D ~ l o g ( 1 1 + e x p ( u w T v c ) ) \theta = argmax_{\theta}\prod_{(w,c)\in D}P(D=1|w,c,\theta)\prod_{(w,c)\in \tilde{D}}P(D=0|w,c,\theta)\\=argmax_{\theta}\prod_{(w,c)\in D}P(D=1|w,c,\theta)\prod_{(w,c)\in \tilde{D}}(1-P(D=1|w,c,\theta))\\=argmax_{\theta}\sum_{(w,c)\in D}logP(D=1|w,c,\theta)+\sum_{(w,c)\in \tilde{D}}log(1-P(D=1|w,c,\theta))\\=argmax_{\theta}\sum_{(w,c)\in D}log\frac{1}{1+exp(-u_w^Tv_c)}+\sum_{(w,c)\in \tilde{D}}log(1-\frac{1}{1+exp(-u_w^Tv_c)})\\=argmax_{\theta}\sum_{(w,c)\in D}log\frac{1}{1+exp(-u_w^Tv_c)}+\sum_{(w,c)\in \tilde{D}}log(\frac{1}{1+exp(u_w^Tv_c)}) θ=argmaxθ(w,c)∈D∏P(D=1∣w,c,θ)(w,c)∈D~∏P(D=0∣w,c,θ)=argmaxθ(w,c)∈D∏P(D=1∣w,c,θ)(w,c)∈D~∏(1−P(D=1∣w,c,θ))=argmaxθ(w,c)∈D∑logP(D=1∣w,c,θ)+(w,c)∈D~∑log(1−P(D=1∣w,c,θ))=argmaxθ(w,c)∈D∑log1+exp(−uwTvc)1+(w,c)∈D~∑log(1−1+exp(−uwTvc)1)=argmaxθ(w,c)∈D∑log1+exp(−uwTvc)1+(w,c)∈D~∑log(1+exp(uwTvc)1)进而损失函数为: J = − ∑ ( w , c ) ∈ D l o g 1 1 + e x p ( − u w T v c ) + ∑ ( w , c ) ∈ D ~ l o g ( 1 1 + e x p ( u w T v c ) ) J=-\sum_{(w,c)\in D}log\frac{1}{1+exp(-u_w^Tv_c)}+\sum_{(w,c)\in \tilde{D}}log(\frac{1}{1+exp(u_w^Tv_c)}) J=−(w,c)∈D∑log1+exp(−uwTvc)1+(w,c)∈D~∑log(1+exp(uwTvc)1) softmax的改进:分层softmax 一般而言,分层softmax适用于对非常用词,非频繁词的改进,而负采样则更适用于频繁词即低纬向量。 分层softmax的思想是根据词频构造一棵二叉树,词汇越频繁,该词汇对应的叶节点距离根节点就越近。每次需要根据一个给定的词去预测另外一个词时,只需要对二叉树上位于被预测的词路径上的节点向量进行更新。因此,对于频繁词汇的更新比较快速,且整个模型的算法复杂度低。 给定词汇 w i w_i wi预测词汇 w w w的概率为 P ( w ∣ w i ) = ∏ j = 1 L ( w ) − 1 σ ( [ n ( w , j + 1 ) = c h ( n ( w , j ) ) ] v n ( w , j ) T v w i ) P (w|w_i)=\prod_{j=1}^{L(w)-1}\sigma([n(w,j+1)=ch(n(w,j))]v_{n(w,j)}^Tv_{w_i}) P(w∣wi)=j=1∏L(w)−1σ([n(w,j+1)=ch(n(w,j))]vn(w,j)Tvwi)其中, σ \sigma σ表示sigmoid函数, L ( w ) L(w) L(w)代表从根节点到词汇w的叶节点路径上所需要经过的节点总数。 n ( w , j ) n(w,j) n(w,j)表示从根节点到词汇w叶节点路径上的第j个节点,其中 n ( w , 1 ) n(w,1) n(w,1)表示根节点。 c h ( ) ch() ch()表示某一个节点的子节点,可能是左子节点也可能是右子节点。函数 [ x ] [x] [x]的含义是,当x为真时,该函数值取1,否则取0, v n ( w , j ) v_{n(w,j)} vn(w,j)是节点 n ( w , j ) n(w,j) n(w,j)的向量表示,即需要学习的向量。 模型训练的目标函数则为 − l o g P ( w ∣ w i ) -logP(w|w_i) −logP(w∣wi),训练过程中只需要对二叉树中位于路径上的节点的向量进行更新。 Question 1.1: Implement distinct_words Question 1.2: Implement compute_co_occurrence_matrix Question 1.3: Implement reduce_to_k_dim Question 1.4: Implement plot_embeddings
独热码向量表示: 向量的维度 = 字典当中单词的个数。
根据字典中单词的个数N构造一个N维的向量,对于第i个单词,在第i维对该单词赋值为1,其余值为零。由于只有一个数字为1,称为独热码,即one-hot vector。
解决方法: 自动学习向量之间的相似性表示,用更低维度的向量来表示每一个单词。
由于单词的意思可以通过上下文来得到反映,因此可以使用单词周边的上下文来对中心词的词表示进行构建。
对每一个单词构建一个密集向量,使得会出现在相同的上下文当中的具有相同含义的词语具有相似的向量表示。基于SVD的方法
这个矩阵构造方法基于一个假设,即认为相似的单词总是会经常在一个文档当中同时出现,所以在构造的时候会遍历所有的M个文档,看字典中的V个单词是否在文档中出现过,对于每个单词i在文档j中出现一次,就对Xij加一。但是这样构造出来的矩阵会十分庞大 X ∈ R V ∗ M X \in \mathbb{R}^{V*M} X∈RV∗M因此需要采用一个更好的X矩阵的构造方式。
这个方法的思想和前面所述的方法类似,但是不再是对所有文档进行遍历,而是对单词窗口内的共现单词进行统计。步骤如下:
(1)构造一个维度V x V的共现矩阵X
(2)对X进行SVD,得到 X = U S V T X = USV^T X=USVT
(3)选择矩阵U的前K列作为K维的单词向量表示
(4)得到K维的向量表示之后, ∑ i = 1 k σ i ∑ i = 1 ∣ V ∣ σ i \frac{\sum_{i=1}^{k}\sigma_i}{\sum_{i=1}^{|V|}\sigma_i} ∑i=1∣V∣σi∑i=1kσi代表该K维向量表示所包含的字典整体的方差比例。
基于迭代的方法 - Word2vec
还包含两种训练方法:负采样(通过采集负样本来构造新的目标函数)分层softmax(使用不对称的树结构来高效地计算每个词出现的概率)CBOW (continuous bag of words)
skip-gram
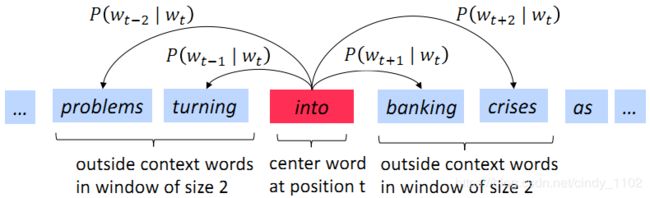
本例中, w t w_t wt = “into”, 是前面提到过的中心词 c.
中心词会随着遍历位置的改变而不断改变 (中心词: “into” --> “banking” --> “crises”…)梯度的推导过程
优化的过程当中会更简单,最后会对两个向量取平均,作为最后的向量表示。skip-gram和CBOW的改进
另外还有一个对softmax进行改进的方法,即分层softmax(hierarchical softmax)Assignment 1 参考代码
def distinct_words(corpus):
""" Determine a list of distinct words for the corpus.
Params:
corpus (list of list of strings): corpus of documents
Return:
corpus_words (list of strings): list of distinct words across the corpus, sorted (using python 'sorted' function)
num_corpus_words (integer): number of distinct words across the corpus
"""
corpus_words = []
num_corpus_words = -1
# ------------------
# Write your implementation here.
flattened_corpus = [y for x in corpus for y in x]
num_corpus_words += 1
for word in flattened_corpus:
if word not in corpus_words:
corpus_words.append(word)
num_corpus_words += 1
corpus_words.sort()
# ------------------
return corpus_words, num_corpus_words
def compute_co_occurrence_matrix(corpus, window_size=4):
""" Compute co-occurrence matrix for the given corpus and window_size (default of 4).
Note: Each word in a document should be at the center of a window. Words near edges will have a smaller
number of co-occurring words.
For example, if we take the document "START All that glitters is not gold END" with window size of 4,
"All" will co-occur with "START", "that", "glitters", "is", and "not".
Params:
corpus (list of list of strings): corpus of documents
window_size (int): size of context window
Return:
M (numpy matrix of shape (number of corpus words, number of corpus words)):
Co-occurence matrix of word counts.
The ordering of the words in the rows/columns should be the same as the ordering of the words given by the distinct_words function.
word2Ind (dict): dictionary that maps word to index (i.e. row/column number) for matrix M.
"""
words, num_words = distinct_words(corpus)
M = None
word2Ind = {}
# ------------------
# Write your implementation here.
flattened_corpus = [y for x in corpus for y in x]
for index, word in enumerate(words):
word2Ind[word] = index
M = np.zeros((len(words),len(words)))
for index, word in enumerate(flattened_corpus):
left = max(0,index-window_size)
right = min(len(flattened_corpus),index+window_size)
for i in range(left,right):
if i != index:
co_word = flattened_corpus[i]
if word in ["START","END"] and co_word in ["STRAT","END"]:
pass
else:
M[word2Ind[word]][word2Ind[co_word]] += 1.
M[word2Ind[co_word]][word2Ind[word]] += 1.
# ------------------
return M, word2Ind
def reduce_to_k_dim(M, k=2):
""" Reduce a co-occurence count matrix of dimensionality (num_corpus_words, num_corpus_words)
to a matrix of dimensionality (num_corpus_words, k) using the following SVD function from Scikit-Learn:
- http://scikit-learn.org/stable/modules/generated/sklearn.decomposition.TruncatedSVD.html
Params:
M (numpy matrix of shape (number of corpus words, number of corpus words)): co-occurence matrix of word counts
k (int): embedding size of each word after dimension reduction
Return:
M_reduced (numpy matrix of shape (number of corpus words, k)): matrix of k-dimensioal word embeddings.
In terms of the SVD from math class, this actually returns U * S
"""
n_iters = 10 # Use this parameter in your call to `TruncatedSVD`
M_reduced = None
print("Running Truncated SVD over %i words..." % (M.shape[0]))
# ------------------
# Write your implementation here.
svd = TruncatedSVD(n_components=k, n_iter=n_iters)
M_reduced = svd.fit_transform(M)
# ------------------
print("Done.")
return M_reduced
def plot_embeddings(M_reduced, word2Ind, words):
""" Plot in a scatterplot the embeddings of the words specified in the list "words".
NOTE: do not plot all the words listed in M_reduced / word2Ind.
Include a label next to each point.
Params:
M_reduced (numpy matrix of shape (number of unique words in the corpus , k)): matrix of k-dimensioal word embeddings
word2Ind (dict): dictionary that maps word to indices for matrix M
words (list of strings): words whose embeddings we want to visualize
"""
# ------------------
# Write your implementation here.
for i,type in enumerate(words):
x = M_reduced[i][0]
y = M_reduced[i][1]
plt.scatter(x, y, marker='x', color='red')
plt.text(x, y, type, fontsize=9)
plt.show()
# ------------------