动态规划应用——盗贼选重物和硬币找零问题的python实现
算法定义:
1.采用更为条理的方式得到问题的最优解
2.从最简单问题的最优解开始,逐步叠加到问题的解法
例如:找零兑换的动态规划解法就是在金额递加时,设法保证每一分钱的递加都是最优解,因此,待到求解金额数,自然得到最优解。
3. 动态规划求解关键条件:问题的最优解包含了更小规模子问题的最优解,其实采用动态规划策略解决的必要条件。
找零问题:动态规划解法
def dpmakechange(coinvaluelist,change,mincoins):
for cents in range(1,change+1): #从1增加到change,逐个计算最少硬币数
coincount=cents #初始化一个最大值
for j in [c for c in coinvaluelist if c<=cents]:
if mincoins[cents-j]+1< coincount:
coincount=mincoins[cents-j]+1
mincoins[cents]=coincount
return mincoins[change]
print(dpmakechange([1,5,10,25],63,[0]*64))
动态规划总结:
- 从最简单的情况开始,直至到达所需找零的循环
- 其中每一步都依靠以前的最优解,来获得本步骤的最优解,直至找到答案
问题拓展:打印出硬币情况
代码实现:
def dpmakechange(coinvaluelist,change,mincoins,coinsused):
for cents in range(1,change+1): #从1增加到change,逐个计算最少硬币数
coincount=cents #初始化一个最大值
newcoin=1 #初始化一个新加硬币
for j in [c for c in coinvaluelist if c<=cents]:
if mincoins[cents-j]+1< coincount:
coincount=mincoins[cents-j]+1
newcoin=j #对应的最下数量,所减的硬币
mincoins[cents]=coincount
coinsused[cents]=newcoin #记录本步骤增加的1个硬币
return mincoins[change]
def printcoins(coinsused,change):
coin=change
while coin >0:
thiscoin=coinsused[coin]
print (thiscoin)
coin=coin-thiscoin
print(dpmakechange([1,5,10,25],63,[0]*64,[0]*64))
## printcoins ([0]*64,63) 陷入死循环,无法停止
小结
对比递归算法和动态规划算法知:动态规划的代码更加简洁,理解起来也更加容易,但递归算法也能解决该类问题
递归调用解法参考博客:https://blog.csdn.net/cy15625010944/article/details/106385008
博物馆大盗问题
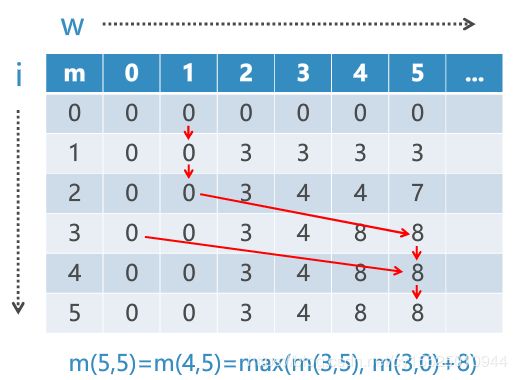
问题描述:大盗潜入博物馆,面前有五件宝贝,分别有重量和价值,可是盗贼背包仅能负重20公斤,请问如何选择宝物,总价值最高?
| item | weight | value |
|---|---|---|
| 1 | 2 | 3 |
| 2 | 3 | 4 |
| 3 | 4 | 8 |
| 4 | 5 | 8 |
| 5 | 9 | 10 |
tr=[None,{'w':2,'v':3},{'w':3,'v':4},{'w':4,'v':8},
{'w':5,'v':8},{'w':9,'v':10}] #宝物的价值
max_w=20 #最大承重量
m={(i,w):0 for i in range(len(tr))
for w in range(max_w+1)} #初始化二维表格
for i in range(1,len(tr)): #逐个填写二维表格
for w in range(1,max_w+1):
if tr[i]['w']> w :
m[(i,w)]=m[(i-1,w)]
else:
m[(i,w)]=max(m[(i-1,w)],m[(i-1,w-tr[i]['w'])]+tr[i]['v'])
#输出结果
print(m[(len(tr)-1,max_w)]) #29
问题拓展:递归调用解法
##博物馆大盗问题
tr={(2,3),(3,4),(4,8),(5,8),(9,10)} #宝物的重量和价值
max_w=20 #最大承重量
m={} #初始化表格 key是(宝物组合,最大重量),value是最大价值
def thief(tr,w):
if tr==set() or w==0:
m[(tuple(tr),w)]=0 #tuple是key的要求
return 0
elif (tuple(tr),w) in m:
return m[(tuple(tr),w)]
else:
vmax=0
for t in tr:
if t[0]<=w: ##逐个去掉某个宝物,递归调用
v=thief(tr-{t},w-t[0])+t[1]
vmax=max(vmax,v)
m[(tuple(tr),w)]=vmax
return vmax
##输出结果
print(thief(tr,max_w))
小结
用动态规划和递归分别解决了博物馆大盗问题,观察知:主要递归和记忆化应用得当,也能高效解决该类问题。