后缀自动机构造后缀树

http://www.elijahqi.win/archives/3945
今天研究一天怎么构造始终想不明白 看到这篇blog之后顿悟

为了帮助其他人避免像蒟蒻我一样 想不明白感到难过

于是随便写一写

要是有错误 qwq麻烦指出

(emm退役之后不知道还会不会上blog)

https://www.cnblogs.com/hehe54321/p/8694839.html

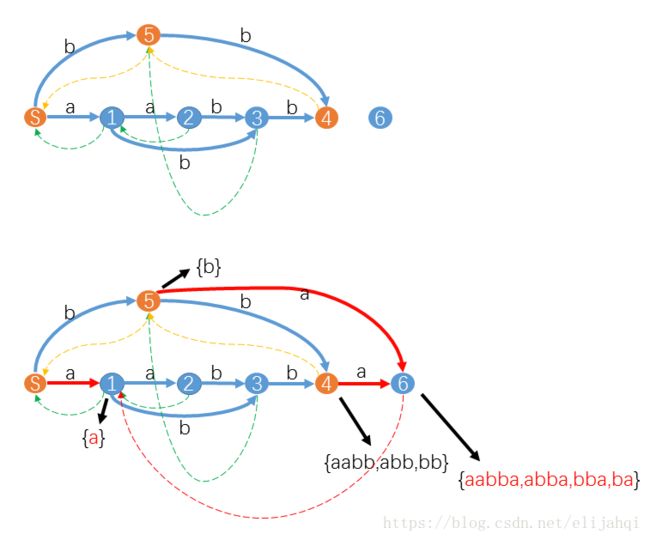
看上面两张图中，上面的那张图：后缀链接对应的后缀树上的边是：

5->S===>b，4->5===>baa，3->5===>aa，2->1===>a，1->s===>a，也就是后缀链接起点能接受的所有长度的串，按长度从小到大排，各取第一个字符组成的串

后缀树的根就是S

从某一节点沿着后缀链接走到S，记录下经过所有边代表的串，翻转序列，连成一个字符串，然后翻转整个字符串，就是该节点在后缀自动机上能接受的最长串

某一节点能接受的最长串为S，则该节点能接受的所有串都是S的后缀，往后缀链接跳一步到的节点能接受的串则也是S的

板子

知道一个性质 sam上的parent树就是反串的后缀树

那么我们要求后缀树的时候把原串反过来建SAM即可 这样保证状态节点数什么的都是线性o(n)

那么我们考虑 后缀自动机 par树的含义是 针对我这个节点所能表示的串的最长后缀的位置

我们参照这个图 反串建立后缀自动机的时候我们尝试沿着par树行走 发现反串的par树其实相当于原串的一些前缀 然后每次跳par树的时候都相当于在找一个后缀的前缀

然后那么如果要看后缀树上表示的边到底压缩了哪些字母我们可以考虑 在后缀自动机上用我当前的节点能表示的最长串-fa[当前节点]表示的最长串 然后将其反过来就是后缀树上压缩的边了
贴一道题:

Lyra 是一个灵巧的女孩子，她特别喜欢玩一种叫“石头剪刀布”的游戏，在这个游戏中，每回合双方同时打出一种手势，为石头(r)，剪刀(s)，布(p)之一，规定石头打败剪刀，剪刀打败布，布打败石头，若手势一样则视为平局。

虽然 Lyra 是一个灵巧的女孩子，她发现她依然赢不了 Evan，潜心研究多日 Evan 的策略后，发现在第二天的 n

n

轮游戏中，Evan 一定以某种固定策略出手势。

这个固定策略（一个长度为 n

n

的由 r,s,p

r,s,p

组成的字符串）就藏在 Evan 的电脑里，被 Evan 加密存储。Evan 的加密方式很奇怪，他先选取一个特定的 d

d

，然后把整个字符串循环右移 d

d

个位置。

Lyra 拿到了加密后的策略串，她想在第二天的石头剪刀布比赛中大败 Evan，注意 Lyra 的策略不一定必须是开始前固定的，可以根据前若干回合的结果修正之后的策略。

在这场石头剪刀布大赛中，对于第 i

i

个回合，获胜可以获得 wi

wi

分，平局获得 di

di

分，而失败获得 0

0

分。Lyra 想知道自己采取最优策略的话，最坏情况下至少从这 n

n

个回合中获得多少分。

输入格式
第一行三个正整数 n

n

表示回合数。

第二行一个长度为 n

n

的字符串 S

S

表示 Evan 的序列的某个轮换。

接下来 n

n

行每行两个整数 wi,di

wi,di

，表示获胜得分，平局得分。

输出格式
一行一个正整数表示 Lyra 至少获得的分数。

样例输入输出
样例输入1
5
rrsrr
3 1
3 1
3 1
3 1
3 1
样例输出1
12
样例输入2
6
rsprsp
3 1
3 1
3 1
3 1
3 1
3 1
样例输出2
15
在苏州训练的时候lzz的一道题 暴力做法就是暴力建出后缀trie之后在trie上dp 对于题意我是理解了很久

其实是在我出的所有方案中 每种方案对应一种最坏的情况 然后我选择这三种情况中最好的一种情况

那么 将串复制一遍 然后在反过来建sam就可以得到后缀树 然后后缀树就是精简之后的后缀trie所以我们在后缀trie上dp可以得到同样的效果 因为这题我们边上只有一种对应的情况所以我们总能赢所以预处理一下能赢的前缀和 到时候减去即可 关于如何确定这个被压缩起来的是哪个我们可以考虑我们现在在sam上的len其实表示的是我原串的一个前缀的长度 所以假如我知道一个节点对应原串的位置我就可以知道他转移到下一个节点是哪里 然后我用我当前位置+下一个节点最长长度-我的最长长度就得到我这条边压缩起来的大小是多少 另外被压缩的字符 恰好就是原串这个对应位置的一个串

#include
#define ll long long
using namespace std;
inline char gc(){
    static char now[1<<16],*S,*T;
    if(T==S){T=(S=now)+fread(now,1,1<<16,stdin);if (T==S) return EOF;}
    return *S++;
}
inline int read(){
    int x=0,f=1;char ch=gc();
    while(!isdigit(ch)) {if (ch=='-') f=-1;ch=gc();}
    while(isdigit(ch)) x=x*10+ch-'0',ch=gc();
    return x*f;
}
const int N=4e5+20;
const ll inf=1ll<<60;
int s[N],last=1,cnt=1,root=1,ch[N][3],len[N],fa[N],p[N];
ll dp[N],pre[N];int n,w[N],d[N],trans[N][3];bool visit[N];
inline void reads(){
    char ch=gc();while(ch!='r'&&ch!='p'&&ch!='s') ch=gc();
    int tot=0;while(ch=='r'||ch=='p'||ch=='s') {++tot;
        if (ch=='r') s[tot]=0;else if (ch=='s') s[tot]=1;
        else s[tot]=2;ch=gc();
    }
}
inline void insert1(int x){
    int p=last,np=++cnt;len[np]=len[p]+1;
    for (;p&&!ch[p][x];p=fa[p]) ch[p][x]=np;
    if (!p) fa[np]=root;else{
        int q=ch[p][x];
        if (len[p]+1==len[q]) fa[np]=q;else{    
            int nq=++cnt;fa[nq]=fa[q];len[nq]=len[p]+1;
            memcpy(ch[nq],ch[q],sizeof(ch[q]));fa[np]=fa[q]=nq;
            for (;p&&ch[p][x]==q;p=fa[p]) ch[p][x]=nq;
        }
    }last=np;
}
inline void init(){
    for (int i=1;i<=n<<1;++i){
        int now=p[i];
        while(!visit[now]){
            int f=fa[now];visit[now]=1;
            trans[f][s[i+len[f]]]=now;now=f;
        }
    }
    for (int i=1;i<=n;++i) pre[i]=pre[i-1]+w[i];
}
inline void dfs(int x){
    if(visit[x]) return;visit[x]=1;
    for (int i=0;i<=2;++i){
        ll mn=inf;
        for (int j=0;j<=2;++j){
            int y=trans[x][j];if (!y) continue;
            ll sum=pre[min(n,len[y])]-pre[len[x]+1];
            if(len[y]if((i+1)%3==j) sum+=w[len[x]+1];
            if(i==j) sum+=d[len[x]+1];
            mn=min(mn,sum);
        }
        dp[x]=max(dp[x],mn);
    }
}
int main(){
    freopen("d.in","r",stdin);
    n=read();reads();
    for (int i=1;i<=n;++i) w[i]=read(),d[i]=read();
    for (int i=n;i;--i) insert1(s[i]),p[i+n]=last;
    for (int i=n;i;--i) insert1(s[i]),p[i]=last,s[i+n]=s[i];
    visit[1]=1;init();memset(visit,0,sizeof(visit));dfs(1);
    printf("%lld\n",dp[1]);
    return 0;
}