《异常监控系统 Kale(skyline&oculus)》

异常监控系统 Kale(skyline&oculus) – 标点符

Kale 系统是 Etsy 公司开源的一个监控分析系统。Kale 分为两个部分：skyline 和 oculus。skyline 负责对时序数据进行概率分布校验，对校验失败率超过阈值的时序数据发报警，oculus 负责给被报警的时序，找出趋势相似的其他时序作为关联性参考。

Skyline 简介

Skyline 是一个实时的异常监测系统，它被动地接收 metrics 数据，并使用一系列算法自动地判断 metrics 是否异常，此外，用户可以很容易地根据自己应用数据的特点，提供自己的异常检测算法。Skyline 还提供了一个 web Ui 接口，异常的 metrics 会在 webapp 中得到展示。

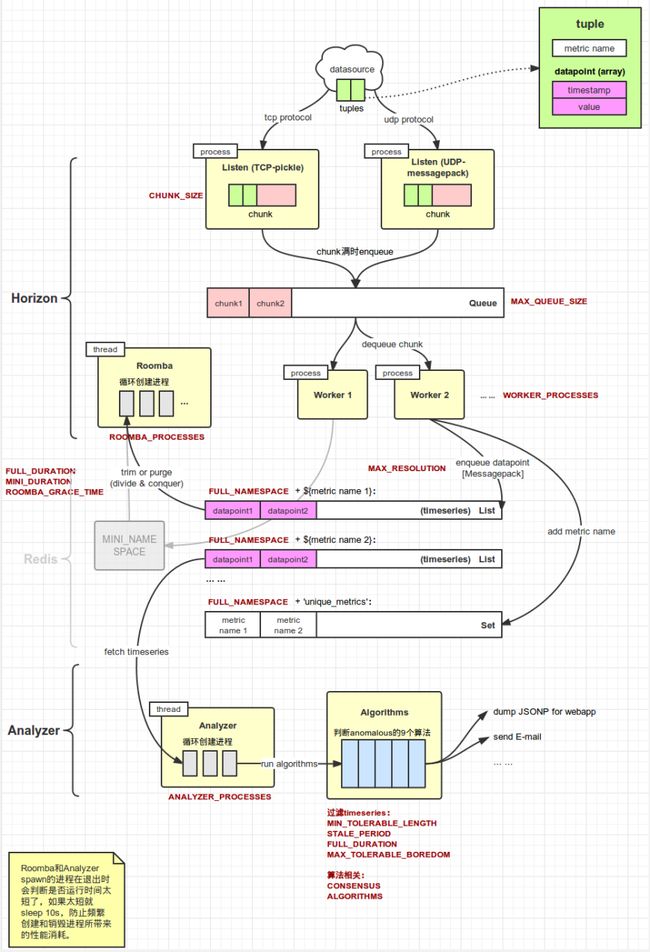
Skyline 内部由 3 个组件组成：Horizon、Analyzer、Webapp。Horizon 负责接收外部发送过来的 datapoint 并转发到 Redis，同时从 Redis 中删除过时的 datapoint（所谓 datapoint 是指某个 metric 在一个特定时间点的数据，它包含 timestamp 和 value）。Analyzer 从 Redis 获取 metrics 数据，并使用算法判断是否异常。最后 Webapp 以图表的方式向用户展示异常的 metrics。Horizon 和 Analyzer 的工作流程如下图所示，红色字体标注的是 settings.py 中定义的配置项：

 

 

Horizon

Horizon 是 Skyline 的数据收集器，它由 3 个角色组成：Listener、Worker、Roomba。Horizon 通过 bin/horizon.d 启停。

Listener

Listener 负责接收外部发送过来的数据，每个 Listener 是一个进程，目前会启动两种类型的 Listener：TCP 和 UDP，它们使用的应用层协议不同，且数据的序列化方式也不同。应用向 horizon 发送 metric 数据时是以 tuple 为单位的，一个 tuple 的格式如下所示，表示某个 metric 在某个时刻的值：

 

 

 

Python

 

1	tuple == (metric_name, datapoint) == (metric_name, [timestamp,value])

TCP pickle

TCP 类型的 Listener 使用的序列化方式是 cPickle，应用层协议如下：

 

 

 

 

Python

 

1 2 3

+----------------------------+-------------------------------------------------------------------------------+ | length(4 bytes)            | [ [tuple1,tuple2...(of metric 'A')], [tuple1,tuple2...(of metric 'B')], ...]  | +----------------------------+-------------------------------------------------------------------------------+

前 4 个字节是 length，表示后续数据的长度。接下来是一个使用 cPickle 序列化的数组，tuple 根据 metric name 分组，每组是该数组内的一个元素。

UDP messagepack

UDP 类型的 Listener 使用的序列化方式是 msgpack，应用层协议为：

 

 

 

Python

 

1 2 3

+---------+ |  tuple  | +---------+

是的，很简单，把 tuple 用 msgpack 序列化后发送即可。因为 UDP 可以保持消息边界的特性，因此不需要 length 字段。

Listener 接收 datapoint 后将其缓存在内部的 Chunk 队列中，其长度由 CHUNK_SIZE 决定；Chunk 满后被放入一个公共的队列 Queue 中，该队列的长度为 MAX_QUEUE_SIZE。

Worker

Worker 负责处理公共队列 Queue 中的 Chunk，Horizon 在启动时会创建 WORKER_PROCESSES 个 worker 进程，不停地从 Queue 中出队 Chunk，将 Chunk 内的 datapoint 经 msgpack 序列化后，按其所属的 metric 添加到对应的 Redis 队列中。

Skyline 在 Redis 中定义了两个 namespace：FULL_NAMESPACE 和 MINI_NAMESPACE，MINI 的作用稍微次要一点，我们先忽略它，后面提及 Roomba 时再讲解。两个 namespace 下的结构都是一致的：

 

 

 

 

Python

 

1	FULL_NAMESPACE + ${metric name} ==> List [ datapoint1,datapoint2,datapoint3 …] (timeseries)

每个 metric 都有一个 List 保存着它所对应的 datapoint 集合，这个 List 在 Skyline 中又被称为 timeseries，它保存着该 metric 在一段时间内的取值序列。

 

 

 

Python

 

1	FULL_NAMESPACE + 'unique_metrics' ==> Set [metric name 1, metric name 2, …]

该 Set 保存着所有 metric 的名字以便快速查找。

Worker 根据 Chunk 内 tuple 所携带的 metric name 信息，将 datapoint 发送到 Redis 的两个 namespace 中以供 Analyzer 模块分析。

Roomba

Roomba 负责清除 Redis 各 timeseries 中过时的 datapoint，只留下最近某段时间内的 datapoint，保证 Redis 不爆掉。Horizon 启动时会启动 Roomba 线程（Roomba 和 Worker 不太一样，它是继承 Thread 的，虽然它的实际工作都是靠创建的进程完成的），对 FULL 和 MINI 两个 namespace 分别创建 ROOMBA_PROCESSES 个进程，从 FULL/MINI_NAMESPACE + ‘unique_metrics’ 中找到所有的 metrics 并均匀地分配给每个进程处理。后者对每个分配的 timeseries，删除距当前 FULL/MINI_DURATION + ROOMBA_GRACE_TIME 秒前的 datapoint；如果整个 timeseries 都过时了，则该 metric 的 List 会从 Redis 中删除，同时 metric name 也会从 set 中删除。

所有进程都退出后，Roomba 线程继续循环，即将进行下一轮进程的创建。为了防止 Redis 中数据很少时，进程快速的创建和退出带来的性能消耗，每个进程在退出时都会判断运行的时间，如果小于 30s，则休眠 10s。

因此，Roomba 的工作其实就是保证 Redis 两个 namespace 下各个 timeseries 始终是 “最近的” 一段数据，其时间跨度由 FULL_DURATION/MINI_DURATION（以及 ROOMBA_GRACE_TIME）指定。FULL 命名空间下的 timeseries 是 Analyzer 分析的对象，MINI 下的并不会被分析，它的作用只在于在 web UI 中为用户提供某个 metric 最近一个小时间段（MINI_DURATION）内的概览。此外，MINI namespace 还用于和 Oculus 配合工作，Oculus 是 Esty 公司出品的另一个系统，我们这里忽略掉。

Analyzer

经过 Horizon 的处理，Redis 中已经保存了若干 timeseries，Analyzer 负责对其进行分析，同时提供了一系列算法判断 timeseries 是否异常的（anomalous）。

Analyzer

Analyzer 也是一个线程，它的工作方式和 Roomba 几乎一致，启动后创建 ANALYZER_PROCESSES 个进程，平均分配 FULL_NAMESPACE 下的所有 timeseries，每个 timeseries 被送入 Algorithms 模块处理，判断是否异常并返回异常的 datapoint、报告异常的算法。

所有进程分析完毕后，Analyzer 将异常 metrics 的相关信息 dump 到 webapp 的 anomalies.json 文件中，随后 webapp 将会通过 JSONP 请求该文件，得到异常信息并展示。此外，Analyzer 还将根据配置的 Email 信息发送预警邮件。

最后，Analyzer 线程判断整个分析过程耗时，如果 < 5s，则休眠 10s，醒后重新进入下一轮进程创建。这里和 Roomba 有点差别，Roomba 的休眠由各个进程判断，而这里是由 Analyzer 线程进行。

Algorithms

这里是判断异常的核心所在，Skyline 内置了 9 个算法来判断一个 datapoint 序列是否异常，用户可以根据自己应用的特征配置要使用的算法（ALGORITHMS 配置项），或者自定义自己的判定算法。

run_selected_algorithm(timeseries) 方法中，timeseries 首先会经过一系列合法性验证：

• datapoint 数目太少（< MIN_TOLERABLE_LENGTH）：TooShort 异常
• 过时（最后一个 datapoint 在 STALE_PERIOD 秒前）：Stable 异常
• 时间跨度太短（两端 datapoint 时间之差 < FULL_DURATION）：Incomplete 异常
• 重复数据太多（最后 MAX_TOLERABLE_BOREDOM 个 datapoint 都是一个值）：Boring 异常

验证后将 timeseries 送入所选算法中进行异常判断。每个算法都会返回 Boolean 值，true 表示异常，false 表示正常。当有 > CONSENSUS 个算法判断为异常时，该 timeseries 才会被认为是 anomalous 的。最终返回 3 个值：是否异常 | 判定为异常的算法集合 | 异常 datapoint，异常 datapoint 目前统一为序列最后 3 个 datapoint 的平均值，这和判断异常的算法是相关的，关于 Skyline 内置的 9 个算法的分析参见这里。

Webapp

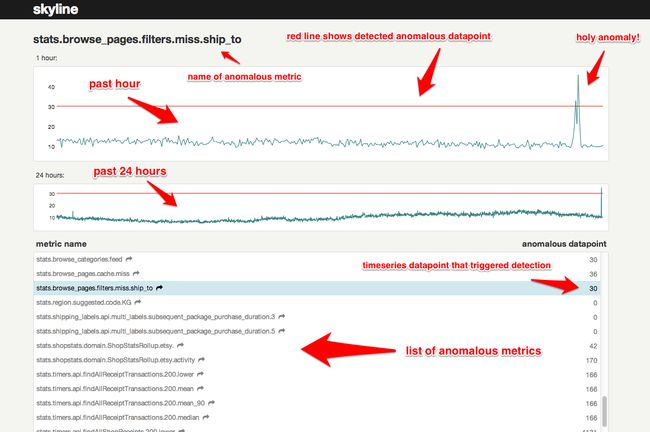
Webapp 基于 Flask 框架提供异常 metrics 的图表展现，是一个比较简单的模块，就不展开了。基本原理是向后台轮询 anomalies.json，得到异常的 metrics 名称及对应的异常 datapoint，之后根据 metrics name 向后台请求 Redis 中的 timeseries 序列（包括 FULL/MINI namespace），并用图表展示出来。借用官网的一张图：

 

 

需要一提的是，图中所示 1 hour 和 24 hour 下的图表，分别是从 MINI 和 FULL NAMESPACE 中取得的 timeseries 数据，它们的时间跨度分别由参数 MINI_DURATION 和 FULL_DURATION 决定，并非固定的 1 小时或 24 小时，只不过页面上是这么写死的。

其他版本：

• etsy 开源版 (9 个检测器，简单投票)：https://github.com/etsy/skyline
• etsy 未开源版的介绍 (小波分解后分别过 KS 和广义 ESD 检验)：https://vimeo.com/131581331
• lytics 公司用 golang 重写的：https://github.com/lytics/anomalyzer
• 社区版 (加入 Ionosphere 模块做反馈修正，使用 tsfresh 库)：https://github.com/earthgecko/skyline
• 360 公司开源的异常检测，和 skyline 一样简单投票，不过自己另写了几个 EWMA、iForest、同环比等检测器：https://github.com/jixinpu/aiopstools/tree/master/aiopstools/anomaly_detection

Skyline 异常判定算法

同样作为时间序列存储的 rrdtool 和 graphite，都偏重在预测算法，也就是说根据现有数据推测下一个数据应该是多少，而 skyline 则是根据现有数据统计最新数据是否异常。

Skyline 内部提供了预定义的算法，这些算法要解决这样一个问题：

• input：一个 timeseries
• output：是否异常

异常检测算法实际写在了 src/analyzer/algorithms.py 里。

3-sigma

一个很直接的异常判定思路是，拿最新 3 个 datapoint 的平均值（tail_avg 方法）和整个序列比较，看是否偏离总体平均水平太多。怎样算 “太多” 呢，因为 standard deviation 表示集合中元素到 mean 的平均偏移距离，因此最简单就是和它进行比较。这里涉及到 3-sigma 理论：

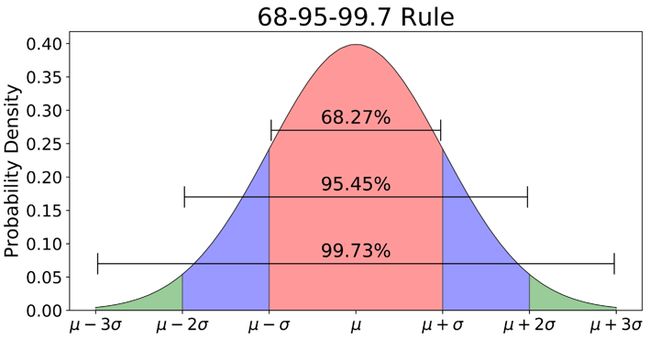
In statistics, the 68-95-99.7 rule, also known as the three-sigma rule or empirical rule, states that nearly all values lie within 3 standard deviations of the mean in a normal distribution.

About 68.27% of the values lie within 1 standard deviation of the mean. Similarly, about 95.45% of the values lie within 2 standard deviations of the mean. Nearly all (99.73%) of the values lie within 3 standard deviations of the mean.

 

 

简单来说就是：在 normal distribution（正态分布）中，99.73% 的数据都在偏离 mean 3 个σ(standard deviation 标准差) 的范围内。如果某些 datapoint 到 mean 的距离超过这个范围，则认为是异常的。Skyline 初始内置的算法几乎都是基于该理论的：

median_absolute_deviation

 

 

 

Python

 

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22

def median_absolute_deviation(timeseries):     """     A timeseries is anomalous if the deviation of its latest datapoint with     respect to the median is X times larger than the median of deviations.     """       series = pandas.Series([x[1] for x in timeseries])     median = series.median()     demedianed = np.abs(series - median)     median_deviation = demedianed.median()       # The test statistic is infinite when the median is zero,     # so it becomes super sensitive. We play it safe and skip when this happens.     if median_deviation == 0:         return False       test_statistic = demedianed.iget(-1) / median_deviation       # Completely arbitary...triggers if the median deviation is     # 6 times bigger than the median     if test_statistic > 6:         return True

具体实现是：序列的最后一个值，比该序列的绝对中值大 6 倍以上，即判断为异常。注意这里是中值，不是平均值。

该算法的优势在于对异常更加敏感：假设 metric 突然变很高并保持一段时间，基于标准差的算法可能在异常出现较短时间后即判断为正常，因为少量 outlier 对标准差的计算是有影响的；而计算 MAD 时，若异常 datapoint 较少会直接忽略，因此感知异常的时间会更长。但正如 Median 的局限性，该算法对于由多个 cluster 组成的数据集，即数据分布在几个差距较大的区间内，效果很差，很容易误判。

grubbs

 

 

 

 

Python

 

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

def grubbs(timeseries):     """     A timeseries is anomalous if the Z score is greater than the Grubb's score.     """       series = scipy.array([x[1] for x in timeseries])     stdDev = scipy.std(series)     mean = np.mean(series)     tail_average = tail_avg(timeseries)     z_score = (tail_average - mean) / stdDev     len_series = len(series)     threshold = scipy.stats.t.isf(.05 / (2 * len_series), len_series - 2)     threshold_squared = threshold * threshold     grubbs_score = ((len_series - 1) / np.sqrt(len_series)) * np.sqrt(threshold_squared / (len_series - 2 + threshold_squared))       return z_score > grubbs_score

Grubbs 测试是一种从样本中找出 outlier 的方法，所谓 outlier，是指样本中偏离平均值过远的数据，他们有可能是极端情况下的正常数据，也有可能是测量过程中的错误数据。使用 Grubbs 测试需要总体是正态分布的。

Grubbs 测试步骤如下：

1. 样本从小到大排序；
2. 求样本的 mean 和 dev.；
3. 计算 min/max 与 mean 的差距，更大的那个为可疑值；
4. 求可疑值的 z-score (standard score)，如果大于 Grubbs 临界值，那么就是 outlier；
5. Grubbs 临界值可以查表得到，它由两个值决定：检出水平α（越严格越小），样本数量 n
6. 排除 outlier，对剩余序列循环做 1-5 步骤。

由于这里需要的是异常判定，只需要判断 tail_avg 是否 outlier 即可。

first_hour_average

 

 

 

 

Python

 

1 2 3 4 5 6 7 8 9 10 11 12 13

def first_hour_average(timeseries):     """     Calcuate the simple average over one hour, FULL_DURATION seconds ago.     A timeseries is anomalous if the average of the last three datapoints     are outside of three standard deviations of this value.     """     last_hour_threshold = time() - (FULL_DURATION - 3600)     series = pandas.Series([x[1] for x in timeseries if x[0] < last_hour_threshold])     mean = (series).mean()     stdDev = (series).std()     t = tail_avg(timeseries)       return abs(t - mean) > 3 * stdDev

这是最简单的。先求本周期内最前面的第一个小时的平均值和标准差，然后和最新的三个值的平均值 (tail_avg()，这是后面多数算法都通用的做法) 做比较。如果 tail_avg 和 第一小时平均值的差距大于 3 倍的标准差，那么认定为异常。

stddev_from_average

 

 

 

Python

 

1 2 3 4 5 6 7 8 9 10 11 12 13

def stddev_from_average(timeseries):     """     A timeseries is anomalous if the absolute value of the average of the latest     three datapoint minus the moving average is greater than one standard     deviation of the average. This does not exponentially weight the MA and so     is better for detecting anomalies with respect to the entire series.     """     series = pandas.Series([x[1] for x in timeseries])     mean = series.mean()     stdDev = series.std()     t = tail_avg(timeseries)       return abs(t - mean) > 3 * stdDev

该算法如下：

• 求 timeseries 的 mean
• 求 timeseries 的 standard deviation
• 求 tail_avg 到 mean 的距离，大于 3 倍的标准差则异常。

注释中写着会计算 moving average，但是代码直接计算的 mean，跟 moving average 没有关系。

该算法的特点是可以有效屏蔽 “在一个点上突变到很大的异常值但在下一个点回落到正常水平” 的情况，即屏蔽单点毛刺：因为它使用的是末 3 个点的均值（有效缓和突变），和整个序列比较（均值可能被异常值拉大），导致判断正常。对于需要忽略 “毛刺” 数据的场景而言，该算法比后续的 EWMA/mean_subtraction_cumulation 等算法更适用（当然也可以改造这些算法，用 tail_avg 代替 last datapoint）。

stddev_from_moving_average

 

 

 

Python

 

1 2 3 4 5 6 7 8 9 10 11 12

def stddev_from_moving_average(timeseries):     """     A timeseries is anomalous if the absolute value of the average of the latest     three datapoint minus the moving average is greater than three standard     deviations of the moving average. This is better for finding anomalies with     respect to the short term trends.     """     series = pandas.Series([x[1] for x in timeseries])     expAverage = pandas.stats.moments.ewma(series, com=50)     stdDev = pandas.stats.moments.ewmstd(series, com=50)       return abs(series.iget(-1) - expAverage.iget(-1)) > 3 * stdDev.iget(-1)

该算法先求出最后一个 datapoint 处的 EWMA（Exponentially-weighted moving average）mean/std deviation，然后用最近的 datapoint 和 3-sigma 理论与之进行比对。

mean_subtraction_cumulation

 

 

 

Python

 

1 2 3 4 5 6 7 8 9 10 11 12 13

def mean_subtraction_cumulation(timeseries):     """     A timeseries is anomalous if the value of the next datapoint in the     series is farther than three standard deviations out in cumulative terms     after subtracting the mean from each data point.     """       series = pandas.Series([x[1] if x[1] else 0 for x in timeseries])     series = series - series[0:len(series) - 1].mean()     stdDev = series[0:len(series) - 1].std()     expAverage = pandas.stats.moments.ewma(series, com=15)       return abs(series.iget(-1)) > 3 * stdDev

算法如下：

1. 排除全序列（暂称为 all）最后一个值（last datapoint），求剩余序列（暂称为 rest，.length-2）的 mean；
2. rest 序列中每个元素减去 rest 的 mean，再求 standard deviation；
3. 求 last datapoint 到 rest mean 的距离，即 abs(last datapoint – rest mean)；
4. 判断上述距离是否超过 rest 序列 dev. 的 3 倍。

简单地说，就是用最后一个 datapoint 和剩余序列比较，比较的过程依然遵循 3-sigma。这个算法有 2 个地方很可疑：

1. 求剩余序列的 dev. 时先减去 mean 再求，这一步是多余的，对结果没影响；
2. 虽然用 tail_avg 已经很不科学了，这个算法更进一步，只判断最后一个 datapoint 是否异常，这要求在两次 analysis 间隔中最多只有一个 datapoint 被加入，否则就会丢失数据。

和 stddev_from_average 相比，该算法对于 “毛刺” 判断为异常的概率远大于后者。

least_squares

 

 

 

Python

 

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25

def least_squares(timeseries):     """     A timeseries is anomalous if the average of the last three datapoints     on a projected least squares model is greater than three sigma.     """       x = np.array([t[0] for t in timeseries])     y = np.array([t[1] for t in timeseries])     A = np.vstack([x, np.ones(len(x))]).T     results = np.linalg.lstsq(A, y)     residual = results[1]     m, c = np.linalg.lstsq(A, y)[0]     errors = []     for i, value in enumerate(y):         projected = m * x[i] + c         error = value - projected         errors.append(error)       if len(errors) < 3:         return False       std_dev = scipy.std(errors)     t = (errors[-1] + errors[-2] + errors[-3]) / 3       return abs(t) > std_dev * 3 and round(std_dev) != 0 and round(t) != 0

最小二乘法：对于一个点对序列(,)(xi,yi)，用一条直线去拟合它，如果某直线 Y=aX+b，使得实际值yi和拟合值 $Y_i# 的误差的平方和最小，则该直线为最优的。

算法如下：

1. 用最小二乘法得到一条拟合现有 datapoint value 的直线；
2. 用实际 value 和拟合 value 的差值组成一个新的序列 error；
3. 求该序列的 stdDev，判断序列 error 的 tail_avg 是否 > 3 倍的 stdDev

因为最小二乘法的关系，该算法对直线形的 metrics 比较适用。该算法也有一个问题，在最后判定的时候，不是用 tail_avg 到 error 序列的 mean 的距离，而是直接使用 tail_avg 的值，这无形中缩小了异常判定范围，也不符合 3-sigma。

histogram_bins

 

 

 

Python

 

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25

def histogram_bins(timeseries):     """     A timeseries is anomalous if the average of the last three datapoints falls     into a histogram bin with less than 20 other datapoints (you'll need to tweak     that number depending on your data)       Returns: the size of the bin which contains the tail_avg. Smaller bin size     means more anomalous.     """       series = scipy.array([x[1] for x in timeseries])     t = tail_avg(timeseries)     h = np.histogram(series, bins=15)     bins = h[1]     for index, bin_size in enumerate(h[0]):         if bin_size <= 20:             # Is it in the first bin?             if index == 0:                 if t <= bins[0]:                     return True             # Is it in the current bin?             elif t >= bins[index] and t < bins[index + 1]:                     return True       return False

该算法和以上都不同，它首先将 timeseries 划分成 15 个宽度相等的直方，然后判断 tail_avg 所在直方内的元素是否 <=20，如果是，则异常。直方的个数和元素个数判定需要根据自己的 metrics 调整，不然在数据量小的时候很容易就异常了。

ks_test

 

 

 

 

Python

 

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

def ks_test(timeseries):     """     A timeseries is anomalous if 2 sample Kolmogorov-Smirnov test indicates     that data distribution for last 10 minutes is different from last hour.     It produces false positives on non-stationary series so Augmented     Dickey-Fuller test applied to check for stationarity.     """       hour_ago = time() - 3600     ten_minutes_ago = time() - 600     reference = scipy.array([x[1] for x in timeseries if x[0] >= hour_ago and x[0] < ten_minutes_ago])     probe = scipy.array([x[1] for x in timeseries if x[0] >= ten_minutes_ago])       if reference.size < 20 or probe.size < 20:         return False       ks_d, ks_p_value = scipy.stats.ks_2samp(reference, probe)       if ks_p_value < 0.05 and ks_d > 0.5:         adf = sm.tsa.stattools.adfuller(reference, 10)         if adf[1] < 0.05:             return True       return False

这个算法比较高深，它将 timeseries 分成两段：最近 10min（probe），1 hour 前 -> 10 min 前这 50 分钟内（reference），两个样本通过 Kolmogorov-Smirnov 测试后判断差异是否较大。如果相差较大，则对 refercence 这段样本进行 Augmented Dickey-Fuller 检验（ADF 检验），查看其平稳性，如果是平稳的，说明存在从平稳状态（50 分钟）到另一个差异较大状态（10 分钟）的突变，序列认为是异常的。

Kolmogorov-Smirnov test

典型应用：

• 判断某个样本是否满足某个已知的理论分布，如正态 / 指数 / 均匀 / 泊松分布；
• 判断两个样本背后的总体是否可能有相同的分布，or 两个样本间是否可能来自同一总体， or 两个样本是否有显著差异。

检验返回两个值：D，p-value，不太明白他们的具体含义，Skyline 里当 p-value <0.05 && D> 0.5 时，认为差异显著。

Augmented Dickey-Fuller test (ADF test)

用于检测时间序列的平稳性，当返回的 p-value 小于给定的显著性水平时，序列认为是平稳的，Skyline 取的临界值是 0.05。

is_anomalously_anomalous

 

 

 

 

Python

 

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38

def is_anomalously_anomalous(metric_name, ensemble, datapoint):     """     This method runs a meta-analysis on the metric to determine whether the     metric has a past history of triggering. TODO: weight intervals based on datapoint     """     # We want the datapoint to avoid triggering twice on the same data     new_trigger = [time(), datapoint]       # Get the old history     raw_trigger_history = redis_conn.get('trigger_history.' + metric_name)     if not raw_trigger_history:         redis_conn.set('trigger_history.' + metric_name, packb([(time(), datapoint)]))         return True       trigger_history = unpackb(raw_trigger_history)       # Are we (probably) triggering on the same data?     if (new_trigger[1] == trigger_history[-1][1] and             new_trigger[0] - trigger_history[-1][0] <= 300):                 return False       # Update the history     trigger_history.append(new_trigger)     redis_conn.set('trigger_history.' + metric_name, packb(trigger_history))       # Should we surface the anomaly?     trigger_times = [x[0] for x in trigger_history]     intervals = [         trigger_times[i + 1] - trigger_times[i]         for i, v in enumerate(trigger_times)         if (i + 1) < len(trigger_times)     ]       series = pandas.Series(intervals)     mean = series.mean()     stdDev = series.std()       return abs(intervals[-1] - mean) > 3 * stdDev

oculus 简介

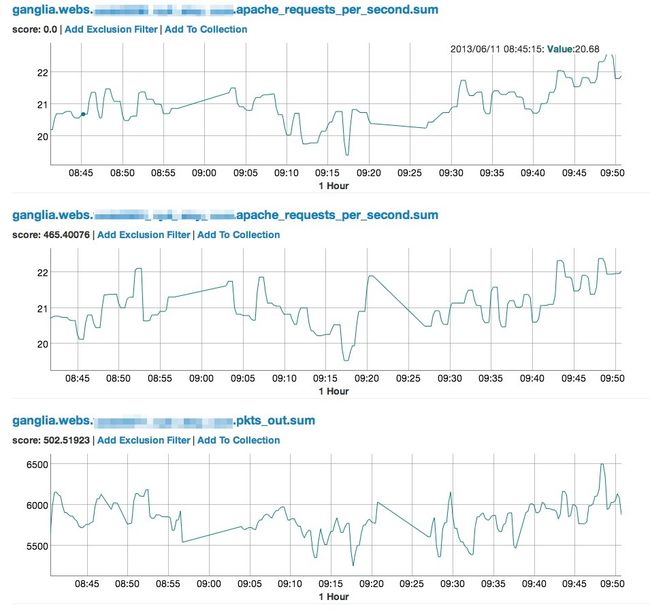
Oculus 的思路，用一句话描述，就是：如果一个监控指标的时间趋势图走势，跟另一个监控指标的趋势图长得比较像，那它们很可能是被同一个根因影响的。那么，如果整体 IT 环境内的时间同步是可靠的，且监控指标的颗粒度比较细的情况下，我们就可能近似的推断：跟一个告警比较像的最早的那个监控指标，应该就是需要重点关注的根因了。

Oculus 截图如下：

 

 

这部分使用的计算方式有两种：

• 欧式距离，就是不同时序数据，在相同时刻做对比。假如 0 分 0 秒，a 和 b 相差 1000，0 分 5 秒，也相差 1000，依次类推。
• DWT 即动态时间规整 (Dynamic Time Warping)，也是时序相似度计算的常用方式，它和欧几里得距离的差别在于，欧几里得距离要求比对的时序数据是一一对应的，而动态时间规整计算的时序数据并不要求长度相等。在运维监控来说，也就是延后一定时间发生的相近趋势也可以以很高的打分项排名靠前。

唯一可惜的是 Etsy 当初实现 Oculus 是基于 ES 的 0.20 版本，后来该版本一直没有更新。现在停留在这么老版本的 ES 用户应该很少了。除了 Oculus，还有很多其他产品，采用不同的统计学原理，达到类似的效果。

参考链接：

• https://github.com/etsy/skyline
• https://github.com/etsy/oculus
• skyline 监控系统工作原理分析

微信支付

支付宝

 

Related Posts

1. Python 学习笔记：针对 list 的数据统计
2. Pandas 学习笔记之分组统计
3. 相似度计算之 Dice 系数
4. 相似度计算之欧几里得距离
5. 使用马氏距离发现异常点

全文完

本文由 简悦 SimpRead 优化，用以提升阅读体验

使用了 全新的简悦词法分析引擎 beta，点击查看详细说明

 

Skyline 简介HorizonAnalyzerWebappSkyline 异常判定算法3-sigmaoculus 简介Related Posts