比特币:一个点对点的电子现金系统
本文由我(samuel)基于2009年Satoshi Nakamoto(中本聪)的论文进行翻译。之前看过别人写的中文翻译,总感觉有点晦涩。现在翻译如下,如有问题,敬请谅解与批评指正!谢谢各位!
0 摘要(Abstract)
一个纯粹p2p的电子现金交易系统能给使得在线支付能够直接由一方发起并支付给另外一方,不需要通过任何的中间的金融机构。虽然数字签名(Digital signatures)提供了部分的解决方案,但是,如果需要第三方支持才能防止双重支付(double-spending)的话,那么这种电子现金也就失去了其价值基础。本文提出了使用p2p网络来解决双重支付(double-spending)的解决方案,p2p网络对全部交易加上时间戳(timestamps),并将其hash到hash-based的工作量证明(proof-of-work)的链条中,生成对应的交易记录(record)。值得注意的是,除非重新完成全部的工作量证明,否则形成的交易记录将不可更改。
最长的链条(或者说最近的区块)不仅仅可以作为从开始到现在所有事件的见证者,而且还被看做是来自CPU计算资源最强大的pool(CPU资源池)中。这个系统基本上是稳定的,唯一可能造成这个系统崩溃的原因:就是有一个人/组织拥有超过整个系统51%的计算能力,那么他就能随意更改每笔交易记录,这就是所谓的“51%攻击”,但这几乎是无法实现的。
另外,p2p网络本身需要内容不多,要求信息尽可能在全网传播,节点(nodes)可以随时离开和重新加入网络,只要其回到网络中的时候,将离开网络这段时间的区块接收并同步即可。
双重支付:在数字货币中,比特币会对前一次的交易和下一位拥有者的公钥签署一个随机散列(hashed)数字签名,将这个签名附加在比特币的末尾发送给下一位所有者。而由于没有第三方机构去做监控,所以需要一个机制去确保比特币之前的所有者没有对更早发生的交易实施签名。
1 介绍(Introduction)
互联网上,几乎所有的交易都需要借助金融机构作为可信赖的第三方来处理。虽然这类系统在绝大多数情况下都运作良好,但是这类系统具有先天不足——受制于“基于信用的模式”(trust based model)。在这种情况下,想要实现不可逆的交易是不现实的,因为金融机构总是不可避免涉及到纠纷调解处理。此外,由于金融中介等第三方的存在,交易的成本也增加了,并且限制了实际可行的最小交易规模和日常的小额支付交易。另外,由于很多商品和服务本身是无法退货的,如果缺乏不可逆的支付手段,互联网的贸易就大大受限。因为交易中有退款的可能,就需要交易双方的互相信任就非常重要了。
因此商家为了提防自己的客户的潜在索赔可能性,经常会向客户提供完全不必要的信息而非关键信息。而实际的商业行为中,带有欺诈目的的客户是不可避免的。在使用现金(physical currency)的情况下,这些销售费用和支付问题上的不确定性却是可以避免的,因为此时没有第三方信用中介的存在。但是目前没有一种用于保证交易在没有可信机构保障下顺利进行的机制( but no mechanism exists to make payments over a communications channel without a trusted party.)。
因此,我们需要一个电子支付系统(基于密码验证/密码学原理而非信用),使得任何达成一致的双方,能够直接进行支付,从而不需要第三方中介的参与。杜绝回滚(reverse)支付交易的可能,这就可以保护特定的卖家免于欺诈;而常规托管机制(routine escrow mechanisms)也有效的保证了买家的权益。在本论文中,我们将提出一种通过点对点分布式的时间戳服务器来生成依照时间前后排列并加以记录的电子交易证明,从而解决双重支付问题。只要诚实节点(honest nodes)所控制的算力的总和大于有合作关系的(cooperating)攻击者的计算能力的总和,那么该系统就是安全的。
2 交易(Transactions)
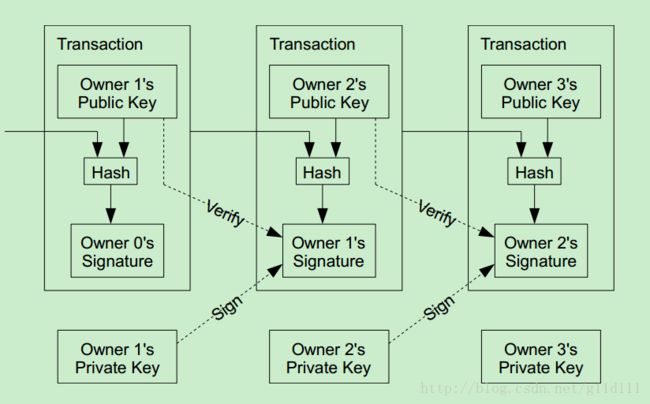
我们将电子coin定义为一个数字签名链(digital signatures)。每个用户的交易都是将前一次交易和交易对象的公钥进行hash得到的数字签名。并将此签名加到coin的末尾。而收款人(payee)通过对签名进行检验,就能够验证该链条的所有者。
该过程的问题在于:收款人难以检验的是:之前的某位所有者有没有对这枚电子货币进行了双重支付。通常的解决方案,就是引入信得过的第三方权威,或者类似于造币厂(mint)的机构,来对每一笔交易进行检验,以防止双重支付。在每一笔交易结束后,这枚电子货币就要被造币厂回收,而造币厂将发行一枚新的电子货币;而只有造币厂直接发行的电子货币,才算作有效,这样就能够防止双重支付。可是该解决方案的问题在于,整个货币系统的命运完全依赖于运作造币厂的公司,因为每一笔交易都要经过该造币厂的确认,而该造币厂就好比是一家银行。
我们需要让收款方(payee)知道之前的拥有者没有在此次交易前的交易签署签名(也就是对已经花出去的钱再次使用···),唯一的方法是需要知道在本次交易之前所有的交易记录。为了排除第三方机构,交易务必要publicly announced。
我们需要整个系统内的所有参与者,都认同唯一的历史交易序列。收款方(payee)需要确保在每次交易期间,大多数的节点都认同该交易是首次出现。
3 时间戳服务器(Timestamp Server)
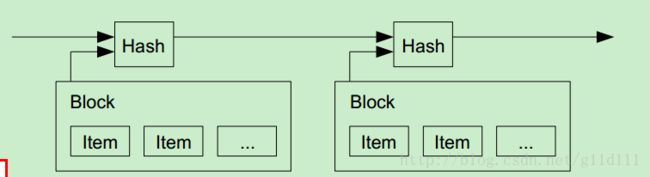
在解决方案的最开始,我们提出了“时间戳服务器”(Timestamp Server)。时间戳服务器通过对以区块(block)形式存在的一组交易记录实施随机散列而加上时间戳,并将该随机散列在系统内进行广播,就像在新闻或世界性新闻组网络(Usenet)的发帖一样。
显然,该时间戳能够证实特定数据在某特定时间确实存在,因为只有在该时刻存在了才有能获取相应的随机散列值。如下图所示,每个时间戳包含在其随机散列中的前一个时间戳,形成了一个链条(Chain)。随后的时间戳会对之前的时间戳进行增强(reinforcing)。
4 工作量证明(Proof-of-Work)
为了实现基于p2p的分布式时间戳服务器,我们需要使用Proof-of-Work系统(跟Adam Back’s 的Hashcash很像)。
在进行随机散列运算时,工作量证明机制引入了对特定值的扫描工作,比方说SHA-256下,随机散列值开头为一个或多个0bit。那么随着0的数目的上升, 找到这个解所需要的工作量将呈指数增长(exponential),而对结果进行检验则仅需要一次随机散列运算。
对于我们的时间戳网络,我们通过对每个Block加入Nonce(随机数)来实现proof-of-work的机制。直到使得这个Block的散列值出现了需要的0bits的情况,才说明这个Block的Nonce被找到。我们通过反复尝试来找到这个随机数(Nonce),直到找到为止,这样我们就构建了工作量证明机制。一旦CPU计算资源开销能够满足该工作量证明机制,那么除非重新完成相当的工作量,该区块的信息就不可更改。由于之后的区块是链接在该区块之后的,所以想要更改该区块中的信息,就需要重新完成(redoing)该区块之后所有区块信息。

工作量证明机制还解决了在集体投票表决(majority decision making)时,谁是大多数(代表)的问题——如果是一个ip一票,那那些拥有很多ip地址的人可能会成为这个系统的权势人物(The Mighty Man)。因此,我们采用的是基于CPU的方式来做工作量证明机制(”one-CPU-one-vote“)。系统中最长的链表示“大多数”的决定,因为最长的链包含了最大的工作量。如果大多数的CPU为诚实节点控制,那么诚实链条将以最快的速度延长,并超越其他的竞争链条。如果想要对业已出现的区块进行修改,攻击者必须重新完成该区块的工作量外加该区块之后所有区块的工作量,并最终赶上和超越诚实节点的工作量。我们将在后面证明,设想一个较慢的攻击者试图赶上随后的区块,那么其成功概率将呈指数递减。
另一个问题是,硬件的运算速度在高速增长,而节点参与网络的程度则会有所起伏。为了解决这个问题,工作量证明的难度机制(the proof-of-work difficulty)将采用移动平均目标的方法来确定,即令难度指向每小时生成区块的速度为某一个预定的平均数。如果区块生成的速度过快,那么难度就会提高。
5 网络(Network)
网络运行的步骤如下:
- (1) 新的交易向全网进行广播;
- (2) 每一个节点都将收到的交易信息纳入一个区块中;
- (3) 每个节点都尝试在自己的区块中找到一个具有足够难度的工作量证明;
- (4) 当一个节点找到了一个工作量证明,它就向全网进行广播;
- (5) 当且仅当包含在该区块中的所有交易都是有效的且之前未存在过的,其他节点才认同该区块的有效性;
- (6) 其他节点表示他们接受该区块是通过在跟随该区块的末尾,制造新的区块以延长该链条,而将被接受区块的随机散列值视为previous的随机散列值。
节点总是认为最长的链是唯一正确的,并且保持区块链的延伸。如果有两个节点同时广播不同版本的新区块,那么其他节点在接收到该区块的时间上将存在先后差别。当此情形,他们将在率先收到的区块基础上进行工作,但也会保留另外一个链条,以防后者变成最长的链条。僵局(tie)的打破要等到下一个工作量证明被发现,而其中的一条链条被证实为是较长的一条,那么在另一条分支链条上工作的节点将转换阵营,开始在较长的链条上工作。
所谓“新的交易要广播”,实际上不需要抵达全部的节点。只要交易信息能够抵达足够多的节点,那么他们将很快被整合进一个区块中。而区块的广播对被丢弃的信息是具有容错能力的。如果一个节点没有收到某特定区块,那么该节点将会在后续接收到区块的情况下,发现自己缺失了后续区块之前的某个区块。
6 激励(Incentive)
本质上:每个区块的第一笔交易是为区块创建者送一个新的bitcoin。可以类比于挖矿,不过消耗的资源变成了CPU时间和电力。这样就会促使更多的节点接入此网络。并提供了一种分发电子货币到流通的原始方式,因为这个系统是去中心化的(decentralized)。
另外一个激励的来源则是交易费(transaction fees)。如果某笔交易的输出值小于输入值,那么差额就是交易费,该交易费将被增加到该区块的激励中。一旦预定数量的电子货币(比特币是2100万枚)已经进入流通,那么激励机制就可以逐渐转换为完全依靠交易费,那么本货币系统就能够免于通货膨胀。
激励系统也有助于节点保持诚实。试想如果有一个贪婪的攻击者能够调集比所有诚实节点加起来还要多的CPU计算力,那么他就面临一个选择:要么将其用于诚实工作产生新的电子货币,或者将其用于进行二次支付攻击。那么他就会发现,按照规则行事、诚实工作是更有利可图的,而进行二次支付攻击的话,那么他自身的货币价值也会受损。
7 回收磁盘空间(Reclaiming Disk Space)
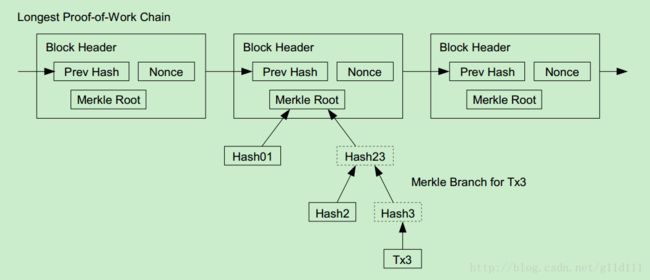
一旦特定的某枚电子货币交易已经被纳入了足够多的区块之中,那么就可以丢弃掉此币(specified coin)交易之前的数据,以回收硬盘空间。为了同时确保不损害区块的随机散列值,交易信息被随机散列时,被构建成一种Merkle树(Merkle tree)的形态,使得只有根(root)被纳入了区块的随机散列值。通过将该树(tree)进行分支拔除(stubbing)的方法,老区块就能被压缩。而内部的随机散列值是不需要保存的。
一个不含交易信息的Block的头(Header)大小仅有80字节。如果我们设定区块生成的速率为每10分钟一个,那么每一年产生的数据为 80∗6∗24∗365=42MB 80 ∗ 6 ∗ 24 ∗ 365 = 42 M B 。以2008年标配电脑2GB内存为例,Moore定律表明内存增长速度约为1.2GB一年,因此Block Header的存储应该不会遇到出现瓶颈的情况。
8 简化支付确认(Simplified Payment Verification)
在本系统中,交易的确认不需要经过所有的网络节点。用户只需要保留一份最长工作量证明的Block Header的复制——通过请求网络直到确认它获得的是最长的链。并且可以通过merkle的分支通向它被加上时间戳并纳入区块的那次交易。用户无法自行检验该交易的有效性,但通过追溯到交易链条的某个位置,用户可以看到某个节点曾经接受过它,并且于其后追加的区块也进一步证明全网曾经接受了它。
这样,只要诚实的节点控制了网络,检验机制就是可靠的。但是,当全网被一个计算力占优的攻击者攻击时,将变得较为脆弱。因为网络节点能够自行确认交易的有效性,只要攻击者能够持续地保持计算力优势,简化的机制会被攻击者伪造的(fabricated)交易欺骗。
一个可行的策略就是,只要他们发现了一个无效区块(invalid block),就立刻发出警报,收到警报的用户将立刻开始下载被警告有问题的区块或交易的完整信息,以便对信息的不一致进行判定。对于每日大量交易产生的商业机构,可能会希望运行他们自己的完整节点,以保持较大的独立完全性和检验的快速性。
9 价值的组合、切分(Combining and Splitting Value)
尽管,我们可以对电子货币的交易进行单独的处理。但实际上,在转让过程中为每一分钱进行单独的交易是很不方便的(比如交易1.2个BTC,我们不能按0.00001BTC为粒度进行交易,这样太耗费Hash散列资源)。为了允许值得合并和拆分,交易可以包含多个输入和输出。
一般而言是某次价值较大的前次交易构成的单一输入,或者由某几个价值较小的前次交易共同构成的并行输入,但是输出最多只有两个:一个用于支付,另一个用于找零(如有,则返回给输入者(sender))。
这里,需要注意的是扇出性(fan-out),即当一笔交易依赖于之前的多笔交易时,而这些交易又各自依赖于多笔交易。但此处这并不构成一个问题,这是因为此工作机制并不需要对之前发生的所有交易历史进行重新检验。
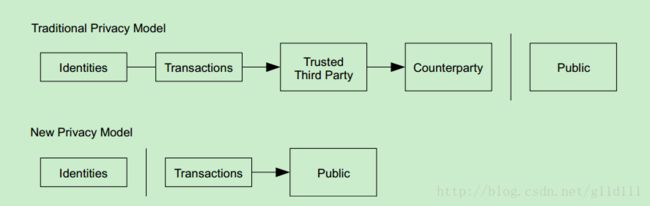
10 隐私(Privacy)
传统的银行模型通过限制当事人向第三方可信机构的获取信息,从而达到一定程度的隐私保护(achieves a level of privacy)。但是如果将交易信息向公开传播,就意味着这种保护隐私的方法失去效力。但是,我们仍然可以通过保护公钥(public keys)匿名来维护隐私:人们可以看到A向B支付了一定的金额,但是没有信息将这笔交易与任何人关联起来。这跟股票交易所发布的信息类似,即:个人的交易时间和交易规模是公开的,但交易当事人是隐藏起来的。
每笔交易都应有一个新的key pair,从而为避免交易者和现实世界的人对应起来增加额外的保护。在多输入交易中,某些链接仍然不可避免(Some linking is still unavoidable),这必然表明它们的输入是由同一所有者拥有的。这里的风险在于,如果此人的某一个公钥被确认属于他,那么就可以追溯出他的其它很多交易。
11 计算(Calculations)
假设一个攻击者试图比诚实节点产生chain更快地制造替代性区块链。即便攻击者达到了这一目的,但是整个系统也并非完全受制于攻击者的掌控之中——比方说凭空创造价值(creating value out of thin air),掠夺本不属于攻击者的货币。这是因为节点不会接受无效的交易,而诚实的节点永远不会接受一个包含了无效信息的区块。所以说,一个攻击者最多可以尝试更改他自己的交易信息,并试图拿回他刚刚付给别人的钱。
诚实链条和攻击者链条之间的长度竞争,可以用二项随机漫步(Binomial Random Walk)来描述。成功事件定义为诚实链条延长了一个区块,使其领先性+1,而失败事件则是攻击者的链条被延长了一个区块,使得差距-1。
攻击者成功填补某一既定差距的可能性,可以近似地看做赌徒破产问题(Gambler’s Ruin problem)。假定一个赌徒拥有无限的透支信用,然后开始进行潜在次数为无穷的赌博,试图填补上自己的亏空(reach breakeven)。那么我们可以计算他填补上亏空的概率,也就是该攻击者赶上诚实链条,如下所示:

这里, p p 是诚实节点找到出下一个区块的概率; q q 为攻击节点找到出下一个区块的概率; qz q z 为攻击节点落后诚实节点z个区块时候能追上的概率。假定 p>q p > q ,那么攻击成功的概率就因为区块数的增长而呈现指数化下降。由于概率是攻击者的敌人,如果他不能幸运且快速地获得成功,那么他获得成功的机会随着时间的流逝就变得愈发渺茫。那么我们考虑一个收款人需要等待多长时间,才能足够确信付款人已经难以更改交易了。我们假设付款人是一个支付攻击者,希望让收款人在一段时间内相信他已经付过款了,然后立即将支付的款项重新支付给自己。虽然收款人届时会发现这一点,但为时已晚。
收款人生成了新的一对密钥组合,然后只预留一个较短的时间将公钥发送给付款人。这将可以防止以下情况:付款人预先准备好一个区块链然后持续地对此区块进行运算,直到运气让他的区块链超越了诚实链条,方才立即执行支付。当此情形,只要交易一旦发出,攻击者就开始秘密地准备一条包含了该交易替代版本的平行链条。
然后收款人将等待交易出现在首个区块中,然后在等到z个区块链接其后。此时,他仍然不能确切知道攻击者已经进展了多少个区块,但是假设诚实区块将耗费平均预期时间以产生一个区块,那么攻击者的潜在进展就是一个泊松分布,分布的期望值为:
现在,为了计算攻击者追赶上诚实节点的概率,我们将攻击者取得进展区块数量的泊松分布的概率密度乘以在该数量下攻击者依然能够追赶上的概率。
将上面的方程进行重新排列,用以避免无限级数求和:
C代码:
#include 对其进行运算,我们可以得到如下的概率结果,发现概率对z值呈指数下降。
当q=0.1时
z=0 P=1.0000000
z=1 P=0.2045873
z=2 P=0.0509779
z=3 P=0.0131722
z=4 P=0.0034552
z=5 P=0.0009137
z=6 P=0.0002428
z=7 P=0.0000647
z=8 P=0.0000173
z=9 P=0.0000046
z=10 P=0.0000012
当q=0.3时
z=0 P=1.0000000
z=5 P=0.1773523
z=10 P=0.0416605
z=15 P=0.0101008
z=20 P=0.0024804
z=25 P=0.0006132
z=30 P=0.0001522
z=35 P=0.0000379
z=40 P=0.0000095
z=45 P=0.0000024
z=50 P=0.0000006
求解令P<0.1%的z值:
为使P<0.001,则
q=0.10 z=5
q=0.15 z=8
q=0.20 z=11
q=0.25 z=15
q=0.30 z=24
q=0.35 z=41
q=0.40 z=89
q=0.45 z=340
12 结论(Conclusion)
本文提出了一种不需要信用中介的电子支付系统。首先从数字签名的一般框架开始讨论,虽然这种系统为电子货币的所有权提供了强有力的控制,但是不足以防止双重支付。
为了解决这个问题,我们提出了一种采用工作量证明机制的点对点网络(p2p)来记录交易的公开信息,只要诚实的节点能够控制绝大多数的CPU计算能力,就能使得攻击者事实上难以改变交易记录。该网络的强健之处在于它结构的简洁。节点之间的工作大部分是相互独立的。在p2p网络中,每个节点不需要证实自己的身份,由于交易信息的流动路径并无任何要求,所以只需要尽其最大努力传播即可。节点可以随时离开网络,而想重新加入网络也非常容易,因为只需要补充接收离开期间的工作量证明链条即可。节点通过自己的CPU计算力进行投票,表决他们对有效区块的确认,他们不断延长有效的区块链来表达自己的确认。任何需要的规则和激励都可以通过这种共识机制(consensus mechanism)来实施。
参考文献(References)
[1] W. Dai, “b-money,” http://www.weidai.com/bmoney.txt, 1998
[2] H. Massias, X.S. Avila, and J.-J. Quisquater, “Design of a secure timestamping service with minimal
trust requirements,” In 20th Symposium on Information Theory in the Benelux, May 1999.
[3] S. Haber, W.S. Stornetta, “How to time-stamp a digital document,” In Journal of Cryptology, vol 3, no 2, pages 99-111, 1991.
[4] D. Bayer, S. Haber, W.S. Stornetta, “Improving the efficiency and reliability of digital time-stamping,” In Sequences II: Methods in Communication, Security and Computer Science, pages 329-334, 1993.
[5] S. Haber, W.S. Stornetta, “Secure names for bit-strings,” In Proceedings of the 4th ACM Conference on Computer and Communications Security, pages 28-35, April 1997.
[6] A. Back, “Hashcash - a denial of service counter-measure,”http://www.hashcash.org/papers/hashcash.pdf, 2002.
[7] R.C. Merkle, “Protocols for public key cryptosystems,” In Proc. 1980 Symposium on Security and Privacy, IEEE Computer Society, pages 122-133, April 1980.
[8] W. Feller, “An introduction to probability theory and its applications,” 1957.