cs224n学习笔记L4: Backpropagation and computation graphs
文章目录
- 课堂安排
- 一、反向传播·续
- 1.1 ∂ s ∂ W \frac{\partial s}{\partial W} ∂W∂s的计算推导
- 1.2 梯度推导温馨提示
- 1.3 输入x的偏导
- 1.4 下游任务更新词向量存在的风险
- 二、计算图及其反向传播
- 2.1 计算图的概念
- 2.2 一个简单地计算实例
- 2.3 分支网络的处理
- 2.5 高效计算:每个局部误差信号仅计算一遍
- 2.6 更复杂的计算图
- 三、神经网络代码实现及相关框架
- 3.1 自动求导
- 3.2 计算图的代码(伪代码)
- 3.3 梯度检查:数值梯度
- 3.4 了解梯度的计算过程的意义
- 四、其他细节
- 4.1 参数正则化
- 4.2 向量化运算
- 4.3 非线性激活函数
- 4.4 参数初始化
- 4.5 优化器
- 4.6 学习率
课堂安排
- 简单网络的梯度计算以及一些小提示
- 计算图和反向传播
- 需要掌握的知识
a. 防止过拟合的规则 b. 向量化 c. 非线性 d. 初始化 e. 优化器 f.学习率
一、反向传播·续
1.1 ∂ s ∂ W \frac{\partial s}{\partial W} ∂W∂s的计算推导
上一节课我们得到:
∂ s ∂ W = δ ∂ z ∂ W \frac { \partial s } { \partial \boldsymbol { W } } = \boldsymbol { \delta }\frac{\partial z}{\partial W} ∂W∂s=δ∂W∂z
假设 z z z长度为n, x x x长度为m,那么我们现在来看看 ∂ z ∂ W \frac{\partial z}{\partial W} ∂W∂z, 由于W是一个n × m的矩阵, 我们单独看一个元素 W i j W_{ij} Wij。由于 W i j W_ij Wij只对 z i z_i zi有影响,因此:
∂ z i ∂ W i j = ∂ ∂ W i j ∑ k = 1 m W i k x k = x j ( 即 j = k 时 的 系 数 ) \frac{\partial z_i}{\partial W_{ij}} = \frac{\partial }{\partial W_{ij}} \sum_{k = 1}^{m}W_{ik}x_k = x_j (即j=k时的系数) ∂Wij∂zi=∂Wij∂k=1∑mWikxk=xj(即j=k时的系数)
所以有:
∂ z i ∂ W = x T \frac{\partial z_i}{\partial W} = x^T ∂W∂zi=xT
那么 ∂ z ∂ W \frac{\partial z}{\partial W} ∂W∂z 就应该是一个n × m的矩阵, 而 ∂ s ∂ W i j = δ i x j \frac{\partial s}{\partial W_{ij}} = \delta_ix_j ∂Wij∂s=δixj , 所以有:
∂ s ∂ W = δ x T [ n × m ] [ n × 1 ] [ 1 × m ] \begin{aligned} & \frac { \partial s } { \partial \boldsymbol { W } } = &\boldsymbol { \delta }&\boldsymbol { x } ^ { T } \\ &[ n \times m ] &[ n \times 1 ]& [ 1 \times m ] \end{aligned} ∂W∂s=[n×m]δ[n×1]xT[1×m]
1.2 梯度推导温馨提示
- 严肃认真的定义变量,并且始终记得维护他们的维度一致性
- 运用链式法则
- 对于顶层的softmax推导,要先考虑 c = y c=y c=y,即正确类别,然后考虑 c ≠ y c \ne y c=y, 即错误类别。
- 如果对矩阵推导感觉迷惑了,就进行元素级别的计算
- 运用维度传播规律,任意一层的误差信号 δ \delta δ的长度与该层的大小相同。
1.3 输入x的偏导
对于x的偏导,输入阶段我们将窗口内的单词拼接成了一个向量,对于反向传播的误差,也可以直接拆分到各个单词向量进行更新。
∇ x J = W T δ \nabla_xJ = W^T\delta ∇xJ=WTδ
如果一个单词在同一个窗口中出现了两次,那么我们就对这个单词进行两次更新。
1.4 下游任务更新词向量存在的风险
假如预训练词向量中有电视、电影、节目三个词义相近,词向量相似的词语,但训练集只有电视、电影两个词出现,而测试集中出现了节目这个词。那么如果我们在训练阶段更新了词向量,就会导致三个词向量之间相似度降低。
解决方案: 如果下游任务数据集较小,就不要更新词向量。如果下游任务数据集很大,那么可以在训练阶段更新词向量(相当于fine-tune)
二、计算图及其反向传播
这之前我们要了解图计算(graph computing) 和 **计算图(computation graph)**是两个不同的概念。本节课的计算图是用图的方式来表示计算流程的神经网络计算框架,而图计算是利用图论方法研究任意数据的内在联系的一类算法统称。
2.1 计算图的概念
- 前向传播(黑色箭头方向):
- 起始节点x为输入
- 每个中间节点为运算操作
- 箭头为运算操作的输出信号
- 反向传播(蓝色箭头方向)
-
每条边代表Loss函数对该层输入信号的偏导(通过链式法则)。
对于单个节点的视图如下:
2.2 一个简单地计算实例
注意这里的max函数,需要跟情况讨论输入参数的梯度,并根据运行反向传播的时刻的输入值来决定使用哪一个梯度(相当于激活的神经元或抑制的神经元)。下图中蓝色部分为反向传播的梯度值,在更新时需要与学习率 α \alpha α相乘。
2.3 分支网络的处理
如果一个节点输出被下一层的多个节点使用,那么反向更新时这个节点就会接受到两个误差信号(如图),我们只需要将这两个输入信号相加(事实上就是多元复合函数求偏导的公式呀)。 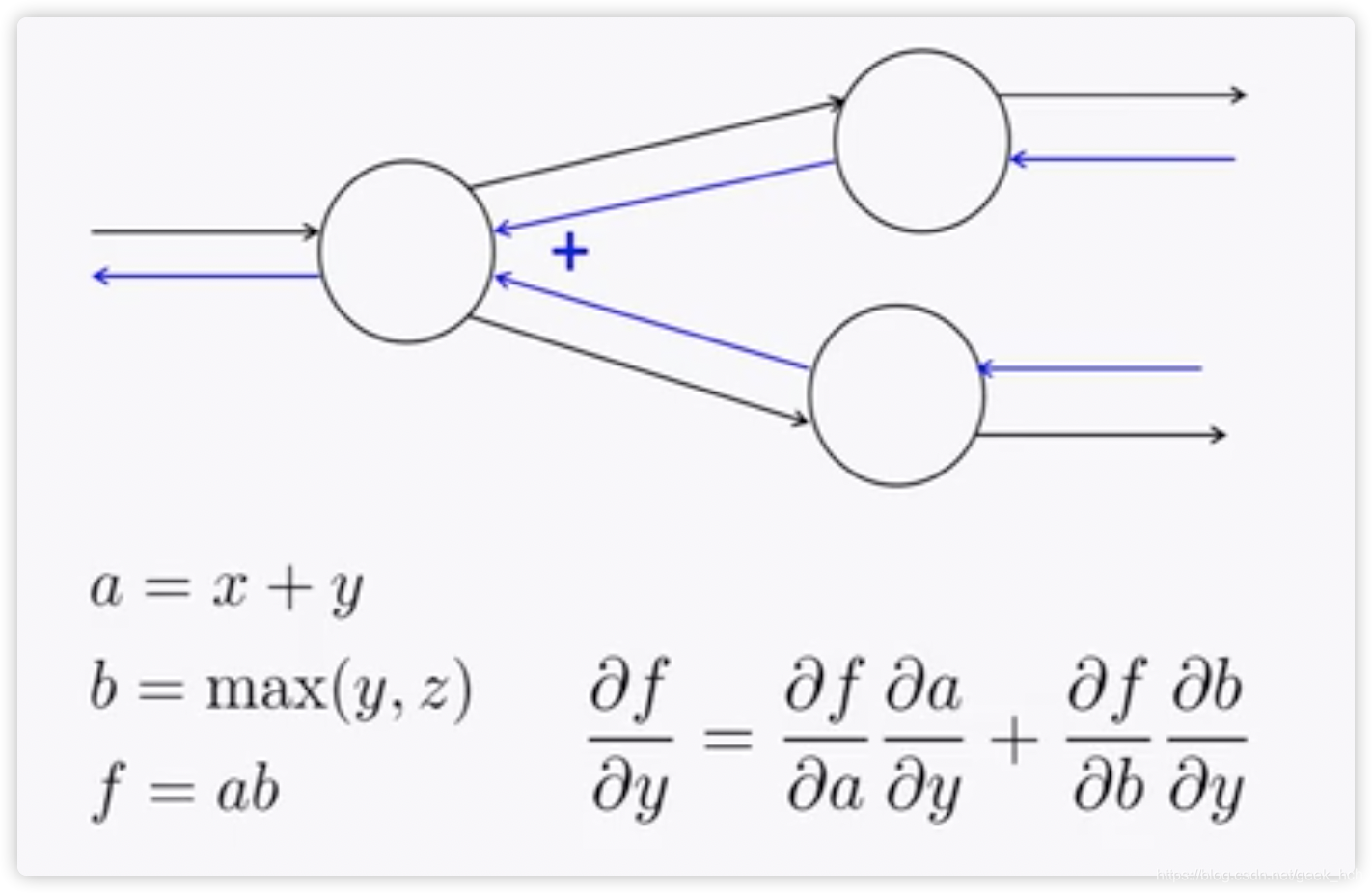 ## 2.4 反向传播运算规律 观察2.2节中的计算过程,可以得出以下规律: + +运算将上游梯度分发复制到下游每个分支 + max运算将上游梯度路由到下游中最大值的那一个分支 + *运算将下游的值交换后作为梯度发送给下游分支。但这只是针对上游分支只有两个的情况。如果有多个呢?(当然就是一个分支的梯度等于其他分支的前向传播值的乘积)
2.5 高效计算:每个局部误差信号仅计算一遍
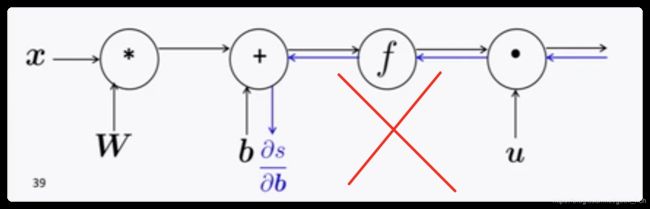
对于如下计算图,如果我们直接计算 ∂ s ∂ b \frac{\partial s}{\partial \boldsymbol{b}} ∂b∂s,这是极其低效的,因为这样的话我们计算 ∂ s ∂ W \frac{\partial s}{\partial \boldsymbol{W}} ∂W∂s时又会重复计算上游的梯度。
高效的计算方式是Top-Down,从loss反向一层层的传播,每一次计算都通过链式法则,利用上一层的梯度信息。
2.6 更复杂的计算图
对于以下计算图,有了前面的知识,我们可以轻易地进行Fprop和Bprop,如果方法正确,Fprop和Bprop的计算复杂度应该相同。根据2.3节:
∂ z ∂ x = ∑ i = 1 n ∂ z ∂ y i ∂ y i ∂ x \frac{\partial z}{\partial \boldsymbol x}=\sum_{i=1}^{n} \frac{\partial z}{\partial y_{i}} \frac{\partial y_{i}}{\partial x} ∂x∂z=i=1∑n∂yi∂z∂x∂yi
对于一些规范的图(大多数神经网络),我们都可以利用矩阵和雅克比来简化计算
三、神经网络代码实现及相关框架
3.1 自动求导
对于每个节点,如果满足下面的条件,那么由这些节点构成的网络就能够自动求导,反向传播。
+ 定义节点的输入与输出
+ 定义该节点输出对每个输入的偏导
现代神经网络框架正式利用这个原理,通过程序员定义每一层/节点的手写梯度计算,来实现整个深度神经网络的自动求导。求偏导公式是一个符号计算过程,tf, torch等框架只提供数值计算,所以需要程序员给出所有可能的计算公式(前向、反向)
3.2 计算图的代码(伪代码)
这是pytorch框架计算图的定义,可以很清晰地看到前向传播、反向传播的逻辑:
对于单个单元,这里以简单的乘法运算为例,实现代码如下,这里要注意forward和backword的接口参数
3.3 梯度检查:数值梯度
(注意区分梯度的数值计算和符号计算)
根据偏导的定义,我们可以通过以下公式计算梯度的近似值,但由于计算中h(1e-4)不是无穷小的数,所以并不是真实的梯度值。
f ′ ( x ) ≈ f ( x + h ) − f ( x − h ) 2 h f ^ { \prime } ( x ) \approx \frac { f ( x + h ) - f ( x - h ) } { 2 h } f′(x)≈2hf(x+h)−f(x−h)
理论上我们可以用这个方法实现完全自动的求导,但我们可以看到这个方法要求每次计算梯度时都要重新计算f(x+h)、f(x-h),并且每次更新对每个参数都要计算一次,性能较低。通常使用这个方法来检查我们的代码实现。
3.4 了解梯度的计算过程的意义
- 有助于我们思考如何提升模型性能
- 可能存在的bug: 梯度消失和爆炸
四、其他细节
4.1 参数正则化
当网络参数量很大的时候,为了防止过拟合,我们需要在一般的loss后面添加一个L2正则项来限制参数。(通过惩罚偏离0较远的参数值,限制模型的拟合能力)
J ( θ ) = 1 N ∑ i = 1 N − log ( e f y i ∑ c = 1 C e f c ) + λ ∑ k θ k 2 J ( \theta ) = \frac { 1 } { N } \sum _ { i = 1 } ^ { N } - \log \left( \frac { e ^ { f _ { y _ { i } } } } { \sum _ { c = 1 } ^ { C } e ^ { f _ { c } } } \right) + \lambda \sum _ { k } \theta _ { k } ^ { 2 } J(θ)=N1i=1∑N−log(∑c=1Cefcefyi)+λk∑θk2
4.2 向量化运算
向量化是指,尽可能的将循环计算转换为更高维的向量计算,因为计算框架对向量运算有优化,比一般的循环快很多。比如下面两行,计算输入和输出一样,但时间却相差了40多倍,如果使用GPU, 差距会远大得多。

4.3 非线性激活函数
早起使用的非线性激活函数如下,其中tanh(z) = 2*sigmod(z) - 1, sigmod 和 tanh现在仍然会在某些特殊情况下被用到,但不再是默认的激活函数:
- sigmod
- tanh
- hard-tanh(出现的原因是为了加速运算,虽然在每一段上都是线性的,但其分段打破了线性,因此是有效的激活函数)
这之后,激活函数不断被改进,出现了更加简化且高效的版本ReLU及其改进版本,ReLU的功能就是简单地赋予神经元(抑制、有效)两种状态,求导非常容易,是在构建网络时推荐的默认激活函数。leaky ReLU只在部分论文中被称有效。
4.4 参数初始化
通常需要将权重初始化为较小的值
- biases初始化为0,
- 其他权重初始化为uniform(-r, r)(r为一个较小的数)
4.5 优化器
一般来说,简单地SGD就会很有效。但一些复杂的网络可能需要适应性更强的优化器,这些优化器可能通过给每个变量设置不同的学习率并记录,来提高其优化效率(Adagrad、RMSprp、Adam(推荐作为默认使用)、sparseAdam)
4.6 学习率
一般默认起始学习率0.001, 可以以10倍减小,太大会导致不收敛,太小则优化过程很慢。
最好允许学习率在学习过程中逐渐减小,比如每k个epoch减半或使用如下公式:
l r = l r 0 e − k t ( t 为 e p o c h ) lr = lr_0e^{-kt}(t为epoch) lr=lr0e−kt(t为epoch)