Coursera上的Andrew Ng《机器学习》学习笔记Week2
Coursera上的Andrew Ng《机器学习》学习笔记Week2
作者:雨水/家辉,日期:2017-01-18,CSDN博客:http://blog.csdn.net/gobitan
Lecture 1: Linear Regression with Multiple Variables多元线性回归
多个参数的线性回归与单参数并没有特别不同。但有一点有所不一样:当有多个参数的时候,如果两个参数的尺度差异太大,会导致收敛速度不一致。可采用feature scaling和mean normalization解决。
梯度下降算法实践:特征尺度(Feature Scaling)和mean normalization 均值归一化
Gradient Descent Practice: Learning Rate
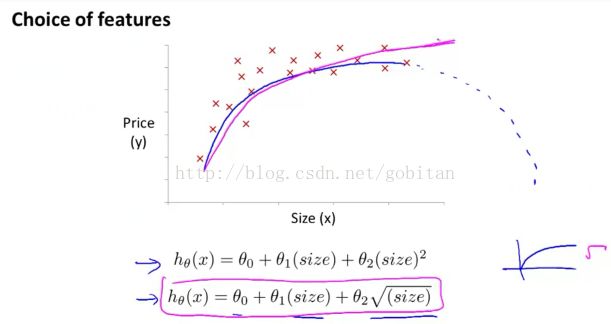
Features and Polynomial Regression(多项式回归)
上图感觉未完全懂?
normal equation标准方程
多元回归的标准方程推导:Xθ=y --> XT Xθ= XT y -->XTX θ= XT y -->(XTX)-1 XTX θ =(XTX)-1 XTY --> θ= (XTX)-1 XTy
Octave的表达:pinv(x'*x)*x'*y
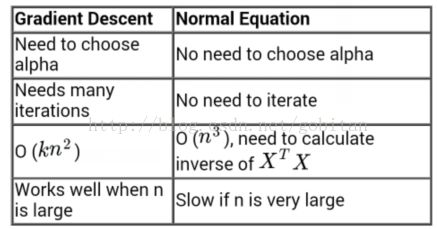
梯度下降算法与标准方程对比:
Normal Equation Noinvertibility 标准方程的不可逆
讲的是(x'*x)不可逆的情况,如:
[1] 冗余的特征(比如参数之间线性依赖)
[2] 参数太多(eg. m<=n) 注:m为样本数,n为特征数
Lecture 2: Octave/Matlab Tutorial
这部分知乎上有比较全的讲解,可参考: https://zhuanlan.zhihu.com/p/22484964 Octave/Matlab教程-Coursera-斯坦福-机器学习
Octave入门
%表示行注释
;表示该行的值不输出,如下所示:
>> a=3;
>> a=3
a = 3
>>
其他例子:
>> a=pi
a = 3.1416
>> disp(a)
3.1416
>> format long
>> a
a = 3.14159265358979
sprintf的使用类似C语言的格式化
矩阵的输入:
>> A=[1 2; 3 4; 5 6]
A =
1 2
3 4
5 6
>>
冒号表达式的规则是告诉octave创建一个以第一个数字开始并以1递增至第二个数的向量。在第一和第 二个数之间可以插入第三个参数来声明向量中元素之间的递增量。如下所示:
>> 1:3
ans =
1 2 3
>> 1:0.5:3
ans =
1.0000 1.5000 2.0000 2.5000 3.0000
>>
>> ones(2,3)
ans =
1 1 1
1 1 1
>> zeros(1,3)
ans =
0 0 0
>>
rand(M,N) 创建一个MXN的矩阵,元素为随机值
hist直方图
diagonal matrix对角矩阵
>> eye(4)
ans =
Diagonal Matrix
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1
>>help eye
Moving Data Around
>>who %查看当前的变量
>>whos %查看当前变量的详情
>>save hello.dat A; %将A保存至hello.dat文件
>>clear A %清除变量A
>>load hello.dat %加载数据文件hello.dat
Computing on data
矩阵乘法A*B
A.*B表示对应的元素相乘,类似写法A.^2表示A的每个元素做平方,1./A表示1除以每个元素
>> A=[1 2; 3 4]
A =
1 2
3 4
>> 1./A
ans =
1.00000 0.50000
0.33333 0.25000
>> log(A)
ans =
0.00000 0.69315
1.09861 1.38629
>>
A(:)将矩阵转为一个向量,如:
>> A(:)
ans =
1
3
2
4
>>
类似的还有指数exp,绝对值abs,直接用负号-作为前缀,最大值max,求和sum
>> B=[1; 2; 3]
B =
1
2
3
>> sum(B)
ans = 6
>>
矩阵的转置A'
A(m:n)表示取向量的第m个元素到第n个元素进行赋值。对于矩阵来说,元素编号是从上到下,从左向右依次编号。
记住两点:
[1] :表示取向量的元素。前面的数字表示开始的序号,后面的数字表示结束的序号。如果数字省略了,前面的默认值就是1,后面默认值就是最后一个;
[2] ,表示索引矩阵中的某个值。前面的数字表示行序号,后面的数字表示列序号。
Plotting Data数据可视化
>> t=[0:0.01:0.98];
>> y1=sin(2*pi*4*t);
>> plot(t,y1) % 画图
>> xlabel('time') % x轴标签
>> ylabel('value') % y轴标签
>> legend('sin') % 图例
>> title('my plot') % 标题
>> print -dpng 'myplot.png' % 保存图
figure用于画多张图,subplot用于多个图画在一张上面。
imagesc用于给矩阵画图
Control Statements: for, while, if statement
for循环语句
>> for i=1:10,
> v(i)=2^i;
> end
while循环语句
>> i = 1;
>> while i<=5,
> v(i) = 100;
> i = i+1;
> end;
if语句
>> if i==1,
disp('The value is one.')
else
disp('The value is not one.')
end;
The value is not one.
>>
定义函数
>> function y = squareThisNumber(x)
y=x^2;
end;
>> squareThisNumber(4)
ans = 16
>>
也可以将函数定义在文件中,文件以m结尾,然后将其路径添加到Octave的路径中。
>> addpath('C:/Users/dhu/Desktop') % 添加搜索路径
成本函数的定义如下所示:
Vectorization向量化
参考资料:
[1] https://www.coursera.org/learn/machine-learning
[2] https://zhuanlan.zhihu.com/p/22484964 Octave/Matlab教程-Coursera-斯坦福-机器学习