Pure Pursuit纯跟踪算法Python/Matlab算法实现
本文的python源代码来自:
https://github.com/gameinskysky/PythonRobotics/blob/master/PathTracking/pure_pursuit/pure_pursuit.py
纯跟踪算法的原理,详见https://blog.csdn.net/gophae/article/details/100012763
我们对纯跟踪算法进行一次仿真,python 我已经改过,如下:
import numpy as np
import math
import matplotlib.pyplot as plt
#定义常数
k = 0.1 # look forward gain
Lfc = 1.0 # look-ahead distance
Kp = 1.0 # speed propotional gain
dt = 0.1 # [s]
L = 2.9 # [m] wheel base of vehicle
show_animation = True
class VehicleState:# 定义一个类,用于调用车辆状态信息
def __init__(self, x=0.0, y=0.0, yaw=0.0, v=0.0):
self.x = x
self.y = y
self.yaw = yaw
self.v = v
def update(state, a, delta):#更新车辆状态信息
state.x = state.x + state.v * math.cos(state.yaw) * dt
state.y = state.y + state.v * math.sin(state.yaw) * dt
state.yaw = state.yaw + state.v / L * math.tan(delta) * dt
state.v = state.v + a * dt
return state
def PIDControl(target, current):#PID控制,定速巡航
a = Kp * (target - current)
return a
def pure_pursuit_control(state, cx, cy, pind):# 纯跟踪控制器
ind = calc_target_index(state, cx, cy)#找到最近点的函数,输出最近点位置
if pind >= ind:
ind = pind
if ind < len(cx):
tx = cx[ind]
ty = cy[ind]
else:
tx = cx[-1]
ty = cy[-1]
ind = len(cx) - 1
alpha = math.atan2(ty - state.y, tx - state.x) - state.yaw
if state.v < 0: # 如果是倒车的话,就要反过来
alpha = math.pi - alpha
Lf = k * state.v + Lfc
delta = math.atan2(2.0 * L * math.sin(alpha) / Lf, 1.0)#核心计算公式
return delta, ind
def calc_target_index(state, cx, cy):
# 找到与车辆当前位置最近点的序号
# search nearest point index
dx = [state.x - icx for icx in cx]
dy = [state.y - icy for icy in cy]
d = [abs(math.sqrt(idx ** 2 + idy ** 2)) for (idx, idy) in zip(dx, dy)]
ind = d.index(min(d))
L = 0.0
Lf = k * state.v + Lfc
# search look ahead target point index
while Lf > L and (ind + 1) < len(cx):
dx = cx[ind + 1] - cx[ind]
dy = cx[ind + 1] - cx[ind]
L += math.sqrt(dx ** 2 + dy ** 2)
ind += 1
return ind
def main():
# target course ,随机出来一条sin函数曲线
cx = np.arange(0, 50, 0.1)
cy = [math.sin(ix / 5.0) * ix / 2.0 for ix in cx]
target_speed = 10.0 / 3.6 # [m/s]
T = 100.0 # max simulation time
# initial state
state = VehicleState(x=-0.0, y=-3.0, yaw=0.0, v=0.0)
lastIndex = len(cx) - 1
time = 0.0
x = [state.x]
y = [state.y]
yaw = [state.yaw]
v = [state.v]
t = [0.0]
target_ind = calc_target_index(state, cx, cy)
# 不断执行更新操作
while T >= time and lastIndex > target_ind:
ai = PIDControl(target_speed, state.v)
di, target_ind = pure_pursuit_control(state, cx, cy, target_ind)
state = update(state, ai, di)
time = time + dt
x.append(state.x)
y.append(state.y)
yaw.append(state.yaw)
v.append(state.v)
t.append(time)
if show_animation:
plt.cla()
plt.plot(cx, cy, ".r", label="course")
plt.plot(x, y, "-b", label="trajectory")
plt.plot(cx[target_ind], cy[target_ind], "xg", label="target")
plt.axis("equal")
plt.grid(True)
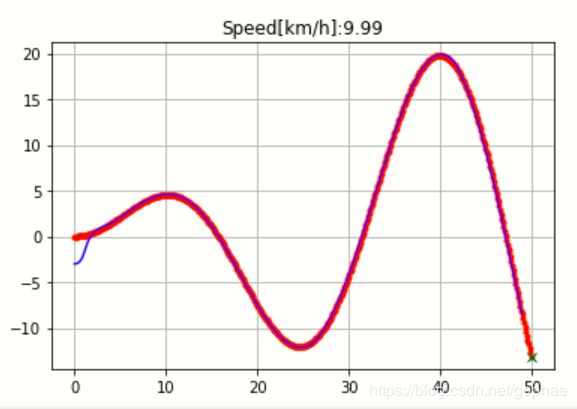
plt.title("Speed[km/h]:" + str(state.v * 3.6)[:4])
plt.pause(0.001)
plt.show()
if __name__ == '__main__':
print("Pure pursuit path tracking simulation start")
main()
将本段代码改为MATLAB版本:
k = 0.1; % look forward gain
Lfc = 1.0; % look-ahead distance
Kp = 1.0 ; % speed propotional gain
dt = 0.1 ;% [s]
L = 2.9 ;% [m] wheel base of vehicle
cx = 0:0.1:50;
cx = cx';
for i = 1:length(cx)
cy(i) = sin(cx(i)/5)*cx(i)/2;
end
i = 1;
target_speed = 10/3.6;
T = 80;
lastIndex = length(cx);
x = 0; y = -3; yaw = 0; v = 0;
time = 0;
Lf = k * v + Lfc;
figure
while T > time
target_ind= calc_target_index(x,y,cx,cy,Lf)
ai = PIDcontrol(target_speed, v,Kp);
di = pure_pursuit_control(x,y,yaw,v,cx,cy,target_ind,k,Lfc,L,Lf);
[x,y,yaw,v] = update(x,y,yaw,v, ai, di,dt,L)
time = time + dt;
% pause(0.1)
plot(cx,cy,'b',x,y,'r-*')
drawnow
hold on
end
% plot(cx,cy,x,y,'*')
% hold on
function [x, y, yaw, v] = update(x, y, yaw, v, a, delta,dt,L)
x = x + v * cos(yaw) * dt;
y = y + v * sin(yaw) * dt;
yaw = yaw + v / L * tan(delta) * dt;
v = v + a * dt;
end
function [a] = PIDcontrol(target_v, current_v, Kp)
a = Kp * (target_v - current_v);
end
function [delta] = pure_pursuit_control(x,y,yaw,v,cx,cy,ind,k,Lfc,L,Lf)
tx = cx(ind);
ty = cy(ind);
alpha = atan((ty-y)/(tx-x))-yaw;
Lf = k * v + Lfc;
delta = atan(2*L * sin(alpha)/Lf) ;
end
function [ind] = calc_target_index(x,y, cx,cy,Lf)
N = length(cx);
Distance = zeros(N,1);
for i = 1:N
Distance(i) = sqrt((cx(i)-x)^2 + (cy(i)-y)^2);
end
[~, location]= min(Distance);
ind = location;
% LL = 0;
% while Lf > LL && (ind + 1) < length(cx)
% dx = cx(ind + 1 )- cx(ind);
% dy = cx(ind + 1) - cx(ind);
% LL = LL + sqrt(dx * 2 + dy * 2);
% ind = ind + 1;
% end
%
ind = ind + 10
end