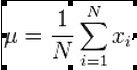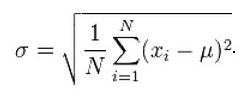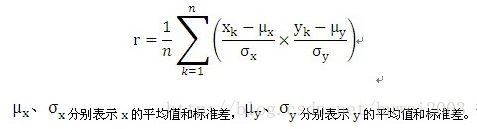相关性、平均值、标准差、相关系数、回归线及最小二乘法
平均值、标准差、相关系数、回归线及最小二乘法
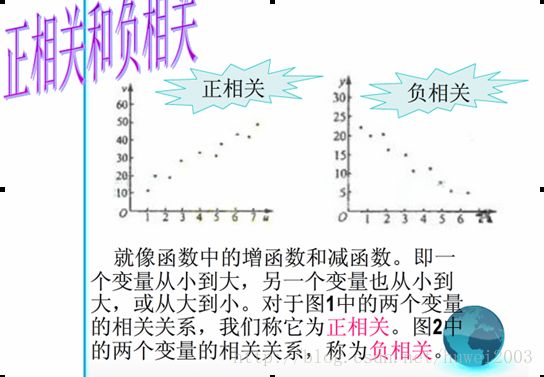
相关性
线性相关
数据在一条直线附近波动,则变量间是线性相关
非线性相关
数据在一条曲线附近波动,则变量间是非线性相关
不相关
数据在图中没有显示任何关系,则不相关
平均值
N个数据 的平均值计算公式:
标准差
标准差表示了所有数据与平均值的平均距离,表示了数据的散度,如果标准差小,表示数据集中在平均值附近,如果标准差大则表示数据离标准差比较远,比较分散。标准差计算公式:
x、y两个变量组成了笛卡尔坐标系中的一个坐标(x,y),这个坐标标识了一个点的位置。
各包含n个常量的X,Y两组数据在笛卡尔坐标系中以n个点来进行表示。
相关系数
相关系数用字母r来表示,表示两组数据线性相关的程度(同时增大或减小的程度),从另一方面度量了点相对于标准差的散布情况,它没有单位。包含n个数值的X、Y两组数据的相关系数r的计算方法:
简单的说,就是 r=[(以标准单位表示的 x )X(以标准单位表示的 y )]的平均数
根据上面点的定义,将X、Y两组数据的关系以点的形式在笛卡尔坐标系中画出,SD线表示了经过中心点(以数据组X、Y平均值为坐标的点),当r>0时,斜率=X的标准差/Y的标准差;当r<0时,斜率=-X的标准差/Y的标准差;的直线。通常用SD线来直观的表示数据的走向:
1、当r<0时,SD线的斜率小于0时,则说明数据负相关,即当x增大时y减少。
2、当r>0时,SD线的斜率大于0时,则说明数据正相关,此时当x增大时y增大。
3、相关系数r的范围在[-1,1]之间,当r=0时表示数据相关系数为0(不相关)。当r=正负1时,表示数据负相关,此(x,y)点数据都在SD线上。
4、r的值越接近正负1说明(x,y)越靠拢SD线,说明数据相关性越强,r的值越接近0说明(x,y)点到SD线的散度越大(越分散),数据相关性越小。
回归方法主要描述一个变量如何依赖于另一个变量。y对应于x的回归线描述了在不同的x值下y的平均值情况,它是这些平均值的光滑形式,如果这些平均值刚好在一条直线上,则这些平均值刚好和回归线重合。通过回归线,我们可以通过x值来预测y值(已知x值下y值的平均值)。下面是y对应于x的回归线方程:
简单的说,就是当x每增加1个SD,平均而言,相应的y增加r个SD。
从方程可以看出:
1、回归线是一条经过点 ,斜率为 的直线。
2、回归线的斜率比SD线小,当r=1或-1时,回归线和SD线重合。
当用回归线从x预测y时,实际值与预测值之间的差异叫预测误差。而均方根误差就是预测误差的均方根。它度量回归预测的精确程度。y关于x的回归线的均方根误差用下面的公式进行计算:
由公式可以看出,当r越接近1或-1时,点越聚集在回归线附近,均方根误差越小;反之r越接近0时,点越分散,均方根误差越大。
最小二乘法寻找一条直线来拟合所有的点,使得这条直线到所有的点之间的均方根误差最小。可以看到,当求两个变量之间的关系时,最小二乘法求出的直线实际上就是回归线。只不过表述的侧重点不同:
1、最小二乘法强调求出所有点的最佳拟合直线。
2、回归线则是在SD线的基础上求出的线,表示了样本中已知变量x的情况下变量y的平均值。
由以上可知,一个散点图可以用五个统计量来描述:
1、所有点x值的平均数,描述了所有点在x轴上的中心点。
2、所有点x值的SD,描述了所有点距离x中心点的散度。
3、所有点y值的平均数,描述了所有点在y轴上的中心点。
4、所有点y值的SD,描述了所有点距离y中心点的散度。
5、相关系数r,基于标准单位,描述了所有点x值和y值之间的关系。
相关系数r将平均值、标准差、回归线这几个概念联系起来:
1、r描述了相对于标准差,点沿SD线的群集程度。
2、r说明了y的平均数如何的依赖于x --- x每增加1个x标准差,平均来说,y将只增加r个y标准差。
3、r通过均方根误差公式,确定了回归预测的精确度。
注意:以上相关系数、回归线、最小二乘法的计算要在以下两个条件下才能成立:
1、x、y两组样本数据是线性的,如果不是线性的先要做转换。
2、被研究的两组样本数据之间的关系必须有意义。