以太坊的挖矿算法、难度调整及代码分析

一、内存依赖挖矿谜题（memory-hard mining puzzle）

对于区块链系统来说，挖矿是保证区块链安全的重要手段（Block chain is secured by mining）。比特币的挖矿算法是比较成功的，经受了时间的考验（一个天然的bug bounty）。

但是比特币的挖矿算法有一些饱受争议的问题，比如只能用ASIC芯片才能挖到矿，这与去中心化背道而驰。理想的挖矿的方式是普通的PC也能参与挖矿，这样算力就能分散开来，发动51%攻击就比较困难了。所以很多加密货币设计mining puzzle的时候，希望能够做到ASIC resistance。

一个比较好的方式是设计出对内存高要求的puzzle，即memory-hard mining puzzle，对于ASIC芯片来说，计算力较强，但在内存访问上的性能没什么优势，所以memory-hard mining puzzle能够遏制ASIC芯片的作用。

1.1 莱特币的Scrypt算法

Scrypt是对内存要求很高（memory-hard）的哈希函数，设计思想是增加对内存的访问，创建一个很大的数组，然后按照顺序填充伪随机数，第一个位置填充从seed运算来的数据，后面每个位置的值都是前一个位置取哈希得到的。这个数组的特点是后面位置的数据依赖前一个数据。

求解puzzle时，按照伪随机的顺序，读取某一个数，根据这个数进行一系列运算，计算出下一个数的位置，读取该位置数据，再根据这个数经过一系列运算得到下一个数的位置，最终可以查看数据是否符合要求。如下图所示：

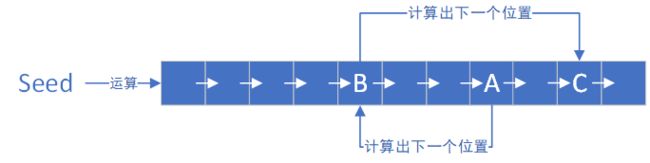
假设这个数组足够大，就必须保存整个数组（或者保存奇数位置数据），才能高效地挖矿；如果不保存数组，那么每次循环都要进行大量地哈希运算，挖矿复杂度将大幅提升。

但是Scrypt的局限性是对于轻节点同样是内存高要求，另外也不能够对谜底进行快速的验证。莱特币在实际运行中，为了照顾轻节点，设置的数组仅有128KB，所以实际并没有达到ASIC resistance的目标。

二、以太坊的挖矿算法（ethash）

2.1 ethash算法介绍

挖矿算法要求难于求解，但是要易于验证（difficult to solve， but easy to verify）。
因此以太坊设计了一个16MB小数据集（cache）和一个1GB的大数据集（dataset），dataset由cache计算而来，矿工保存dataset用于挖矿，轻节点只要保存cache就可以进行验证。

cache的计算方式与与Scrypt类似，通过seed计算出第一个元素，然后依次取哈希，后面位置的数据为前一个位置数据的哈希，这样整个数组就全部填充为伪随机数了。如下图所示：

dataset每个元素都是从cache计算而来，每个元素都是从cached按照伪随机顺序读取一些元素，循环读取256次，即可得到dataset中的一个元素值。如下图所示：

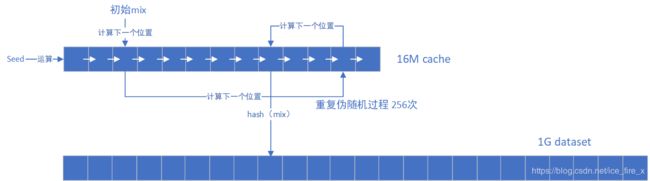
求解puzzle时使用dataset即可，根据区块块头和nonce值算出一个哈希，映射到dataset中一个位置，读取该位置的值，继续按照伪随机的顺序从dataset中循环64次读取128个数（每次读取相邻的2个数），最后算出一个哈希，与target阈值比较 ，看是否符合要求；如果不符合要求则替换nonce值，重复上述过程，直到算出的哈希满足target阈值。如下图所示：

2.2 ethash伪代码分析

def mkcache(cache_size, seed):
    cache = [hash(seed)]
    for i in range(1,cache_size):
        cache.append(hash[cache[-1]])
    return cache

这个函数是通过seed计算出cache的伪代码。
伪代码略去了原来代码中对cache元素进一步的处理，只展示原理，即cache中元素按序生成，每个元素产生时与上一个元素相关。
每隔30000个块会重新生成seed（对原来的seed求哈希值），并且利用新的seed生成新的cache。
cache的初始大小为16M，每隔30000个块重新生成时增大初始大小的1/128 ——128K。

def cal_dataset_i(cahce, i)
    cache_size = cache.size
    mix = hash(cache[i%cache_size]^i)
    for j in range(256):
        cache_index = get_int(mix);
        mix = make_item(mix,cache[cache_index%cache_size])
    return hash(mix)

这是通过cache来生成dataset中第i个元素的伪代码。省略了大部分细节，展示原理。
这个dataset叫作DAG，初始大小是1G，也是每隔30000个块更新，同时增大初始大小的1/128——8M。
先通过cache中的第i%cache_size个元素生成初始的mix，因为两个不同的dataset元素可能对应同一个cache中的元素，为了保证每个初始的mix都不同，注意到i也参与了哈希计算。
随后循环256次，每次通过get_int_from_item来根据当前的mix值求得下一个要访问的cache元素的下标，用这个cache元素和mix通过make_item求得新的mix值。注意到由于初始的mix值都不同，所以访问cache的序列也都是不同的。
最终返回mix的哈希值，得到第i个dataset中的元素。
多次调用这个函数，就可以得到完整的dataset。

def calc_dataset(full_size, cache):
    return [calc_dataset_item(cache,i) for i in range(full_size)]

这个函数通过不断调用前边介绍的calc_dataset_item函数来依次生成dataset中全部full_size个元素。

def hashimoto_full(header, nonce, full_size, dataset):
    mix = hash(header, nonce);
    for i in range(64):
        dataset_index = get_int_from_item(mix) % full_size
        mix = make_item(mix , dataset[dataset_index)
        mix = make_item(mix , dataset[dataset_index + 1])
    return hash(mix)
    
def hashimoto_light(header, nonce, full_size, cache):
    mix = hash(header, nonce)
    for i in range(64):
        dataset_index = get_int(mix)%full_size
        mix = hash(mix, cal_dataset_i(cache,dataset_index))
        mix = hash(mix, cal_dataset_i(cache,dataset_index+1))
    return hash(mix)

这个函数展示了ethash算法的puzzle：通过区块头、nonce以及DAG求出一个与target比较的值，矿工和轻节点使用的实现方法是不一样的。伪代码略去了大部分细节，展示原理。
先通过header和nonce求出一个初始的mix，然后进入64次循环，根据当前的mix值求出要访问的dataset的元素的下标，然后根据这个下标访问dataset中两个连续的的值。
最后返回mix的哈希值，用来和target比较。
注意到轻节点是临时计算出用到的dataset的元素，而矿工是直接访问内存，也就是必须在内存里存着这个1G的dataset，后边会分析这个的原因。

def mine(full_size, dataset, header, target):
    nonce = random.randint(0, 2**64)
    while hashimoto_full(header, nonce, full_size, dataset) > target:
        nonce = (nonce + 1) % 2**64
    return nonce

这是矿工挖矿的函数的伪代码，同样省略了一些细节，展示原理。
full_size指的是dataset的元素个数，dataset就是从cache生成的DAG，header是区块头，target就是挖矿的目标，我们需要调整nonce来使hashimoto_full的返回值小于等于target。
这里先随机初始化nonce，再一个个尝试nonce，直到得到的值小于target。

矿工需要保存整个dataset的原因：
“cache_index = get_int_from_item(mix)”代码表明通过cache生成dataset的元素时，下一个用到的cache中的元素的位置是通过当前用到的cache的元素的值计算得到的，这样具体的访问顺序事先不可预知，满足伪随机性。
由于矿工需要验证非常多的nonce，如果每次都要从16M的cache中重新生成的话，那挖矿的效率就太低了，而且这里面有大量的重复计算：随机选取的dataset的元素中有很多是重复的，可能是之前尝试别的nonce时用过的。所以，矿工采取以空间换时间的策略，把整个dataset保存下来。轻节点由于只验证一个nonce，验证的时候就直接生成要用到的dataset中的元素就行了。

2.3 总结

以太坊的挖矿算法使得矿工主要依靠GPU来挖矿，起到了ASIC resistance的作用。
另外以太坊很早就计划从工作量证明（PoW）转向权益证明（PoS），对于ASIC厂商来说，因为ASIC研发周期最少1年，且成本较高，所以一直没有生产出效率非常高的以太坊ASIC矿机。

一般来说挖矿算法要尽可能让通用计算机参加，挖矿过程越民主，区块链越安全。但是也有一种观点：用通用设备挖矿反而不安全，因为用ASIC芯片发动攻击的成本较高，攻击成功后，反而造成比特币价格下跌。通用设备发动攻击则比较容易，不用专门购买设备，使用原本就在使用的服务器，或者租用云服务器就可以发起攻击。

三、以太坊的挖矿难度调整

比特币是每隔2016个区块调整一次挖矿难度，目标是维持出块时间在10min左右，以太坊中每个区块都会调整出块难度。

3.1 调整公式

调整公式如下所示：
$$D(H)\equiv \{\begin{array}{ll}{D}_0,& if{H}_i=0\\ & \\ max(D_0,P(H{)}_{Hd}+x\times {\varsigma }_2)+ϵ,& otherwise\end{array}$$
$$D_0\equiv 131072$$

• ()是本区块的难度，由基础部分()+×2和难度炸弹部分 相加得到，基础部分维持出块时间大概在15s左右。
• 指的是区块序号
• ()为父区块的难度，每个区块的难度都是在父区块难度的基础上进行调整。
• ×2 用于自适应调节出块难度，维持稳定的出块速度，详见下面的说明。
• 表示设定的难度炸弹，用于向权益证明（PoS）过度。
• 基础部分调整下限为0=131072，保证挖矿的最低难度。

3.2 自适应难度调整×2

自适应难度调整与2部分如下所示：
$$x\equiv \left[\frac{P(H{)}_{Hd}}{2048}\right]$$
$${\varsigma }_2\equiv max\left(y-\left[\frac{H_s-P(H{)}_{Hs}}{9}\right],-99\right)$$

• 是调整的单位，为父区块难度的1/2048，2为调整的系数。
• 是常数，和父区块的uncle数有关。如果父区块中包括了uncle ,为2，否则为1。
  • 父块包含uncle时难度会大一个单位，因为包含uncle时新发行的货币量大，需要适当提高难度以保持货币发行量稳定。
• 难度降低的上界设置为−99 ，主要是应对被黑客攻击或其他目前想不到的黑天鹅事件。所以一次性最多下调99/2048.
• 是本区块的时间戳，()是父区块的时间戳，均以秒为单位，并规定>()。
  • 该部分是稳定出块速度的最重要部分：出块时间过短则调大难度，出块时间过长则调小难度。
  • 以父块不带uncle的情况(=1)为例：
    • 出块时间在[1,8]之间，出块时间过短，难度调大一个单位。
    • 出块时间在[9,17]之间，出块时间可以接受，难度保持不变。
    • 相差时间在[18,26]之间，出块时间过长，难度调小一个单位。
    • …

3.3 难度炸弹

难度炸弹部分如下所示：
$$ϵ\equiv \left[2^{\left[H_i^{\prime }÷100000\right]-2}\right]$$
$$H_i^{\prime }\equiv max(H_i-3000000,0)$$

• 每十万个块扩大一倍，是2的指数函数，到了后期增长非常快，这就是难度“炸弹”的由来。
• 设置难度炸弹的原因是要降低迁移到PoS协议时发生fork的风险：到时挖矿难度非常大，所以矿工有意愿迁移到PoS协议。
• ′称为fake block number，拜占庭（Byzantium）阶段由真正的block number 减少三百万得到。这样做的原因是低估了PoS协议的开发难度，需要延长大概一年半的时间(EIP100)。该值后来又在君士坦丁堡（Constantinople）阶段和Eip2384阶段调整为5000000和9000000。

难度炸弹的威力如下图所示：

降低难度后，出块奖励从5ETH降低为3ETH（君士坦丁堡阶段又降低到了2ETH），否则难度的突然降低会对调整之前挖矿的矿工不公平。

3.4 难度调整代码分析

拜占庭阶段挖矿难度调整的代码实现如下：

// calcDifficultyByzantium is the difficulty adjustment algorithm. It returns
// the difficulty that a new block should have when created at time given the
// parent block's time and difficulty. The calculation uses the Byzantium rules.
func calcDifficultyByzantium(time uint64, parent *types.Header) *big.Int {
	// https://github.com/ethereum/EIPs/issues/100.
	// algorithm:
	// diff = (parent_diff +
	//         (parent_diff / 2048 * max((2 if len(parent.uncles) else 1) - ((timestamp - parent.timestamp) // 9), -99))
	//        ) + 2^(periodCount - 2)

	bigTime := new(big.Int).SetUint64(time)
	bigParentTime := new(big.Int).Set(parent.Time)

	// holds intermediate values to make the algo easier to read & audit
	x := new(big.Int)
	y := new(big.Int)

	// (2 if len(parent_uncles) else 1) - (block_timestamp - parent_timestamp) // 9
	x.Sub(bigTime, bigParentTime)
	x.Div(x, big9)
	if parent.UncleHash == types.EmptyUncleHash {
		x.Sub(big1, x)
	} else {
		x.Sub(big2, x)
	}
	// max((2 if len(parent_uncles) else 1) - (block_timestamp - parent_timestamp) // 9, -99)
	if x.Cmp(bigMinus99) < 0 {
		x.Set(bigMinus99)
	}
	// (parent_diff + parent_diff // 2048 * max(1 - (block_timestamp - parent_timestamp) // 10, -99))
	y.Div(parent.Difficulty, params.DifficultyBoundDivisor)
	x.Mul(y, x)
	x.Add(parent.Difficulty, x)

	// minimum difficulty can ever be (before exponential factor)
	if x.Cmp(params.MinimumDifficulty) < 0 {
		x.Set(params.MinimumDifficulty)
	}
	// calculate a fake block numer for the ice-age delay:
	//   https://github.com/ethereum/EIPs/pull/669
	//   fake_block_number = min(0, block.number - 3_000_000
	fakeBlockNumber := new(big.Int)
	if parent.Number.Cmp(big2999999) >= 0 {
		fakeBlockNumber = fakeBlockNumber.Sub(parent.Number, big2999999) // Note, parent is 1 less than the actual block number
	}
	// for the exponential factor
	periodCount := fakeBlockNumber
	periodCount.Div(periodCount, expDiffPeriod)

	// the exponential factor, commonly referred to as "the bomb"
	// diff = diff + 2^(periodCount - 2)
	if periodCount.Cmp(big1) > 0 {
		y.Sub(periodCount, big2)
		y.Exp(big2, y, nil)
		x.Add(x, y)
	}
	return x
}

函数输入是父区块的时间戳和难度，进行一系列计算后得出当前正在挖的区块难度。

注释中给出的难度公式为：
$$\begin{gathered} diff=(parent\_diff+ \\ (parent\_diff/2048\ast max((2iflen(parent.uncles)else1)-((timestamp-parent.timestamp)//9),-99)))+ \\ {2}^{(}periodCount-2) \end{gathered}$$，与上面章节中所述相同。