总结
今天集齐了四种颜色



这一次真是水翻了,除去第一题送分题,后三道题只拿了50分
开考后完全不在状态,最后的一个半小时一点代码都没有写出来
A、李时珍的皮肤衣
分析
\(n\)的数据最大达到了\(10^{10}\),显然是一道结论题
枚举几组样例可以发现,最终的答案为\(2^{n-1}+1\)对\(n\)取模
其实就是相当于二进制下的进位
因为\(n\)很大,所以要用快速幂
代码
#include
using namespace std;
typedef long long ll;
ll n;
ll ksm(ll now,ll fa){
ll xz=now;
ll ans=1;
while(fa){
if(fa&1){
ans*=xz;
ans=ans%n;
}
fa=(fa>>1);
xz=xz*xz%n;
}
return ans%n;
}
int main(){
scanf("%lld",&n);
printf("%lld\n",(ksm(2,n-1)+1)%n);
return 0;
}
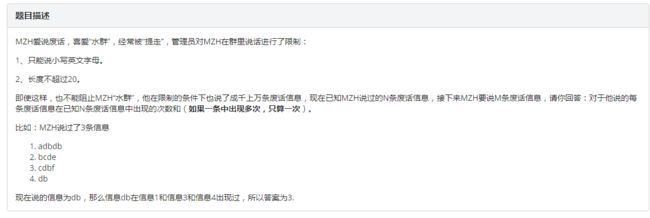
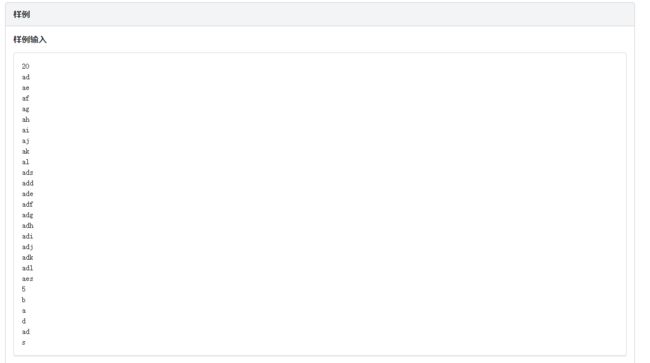
B、马大嘴的废话
分析
如果直接暴力枚举的话可以得到60分
然而暴力写挂了
这道题的最优解要用到AC自动机,但是AC自动机并没有学
林大佬用哈希表过了这道题,但模数比较难取,而且不用c++11会T
其实这一道题可以用Tire树维护
60代码
#include
using namespace std;
const int maxn=20005;
char s[maxn][25];
int main(){
int n;
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%s",s[i]);
}
int m;
scanf("%d",&m);
for(int i=1;i<=m;i++){
char a[25];
scanf("%s",a);
int ans=0;
int now=strlen(a);
int be=0;
for(int j=1;j<=n;j++){
if(strstr(s[j],a)!=NULL) ans++;
}
printf("%d\n",ans);
}
return 0;
}
哈希表代码(林大佬)
#include
#include
#include
#include
#include
#include
using namespace std;
#define ll long long
const ll mod1=2e17+19260817;
const int maxch=43;
const int maxn=2e1+1;
unordered_map mapp1;
vector s1;
unordered_map vis1;
char a[maxn];
int n;
void solve1(int l,int r)
{
ll ans=0,now=1ll;
for(int i=l;i<=r;i++)
{
ans+=now*(a[i]-'a'+1)%mod1,ans%=mod1;
now*=(ll)maxch,now%=mod1;
}
if(vis1[ans]) return;
else vis1[ans]=1,s1.push_back(ans),mapp1[ans]++;
}
int calc1()
{
ll ans=0,now=1ll;
for(int i=0;i Tire树代码
#include
using namespace std;
const int maxn=5e5+10;
int tire[maxn][26],mark[maxn][26],cnt[maxn][26];
int n,m;
int tot=0;
char s[30];
char a[30];
void insert(int l,int r,int id){
int now=0;
int t;
for(int i=l;i<=r;i++){
t=s[i]-'a';
if(tire[now][t]){
if(id!=mark[now][t]){
cnt[now][t]++;
mark[now][t]=id;
}
}
else {
tire[now][t]=++tot;
mark[now][t]=id;
cnt[now][t]=1;
}
now=tire[now][t];
}
}
int query(char a[]){
int len=strlen(a);
int now=0,ans=0;
for(int i=0;i>n;
for(int i=1;i<=n;i++){
cin>>s;
int len=strlen(s);
for(int j=0;j>m;
for(int i=1;i<=m;i++){
cin>>a;
cout< C、SSY的队列
分析
这道题的正解要用哈希表,所以先讲一下部分分的解法
首先就是最简单的暴力枚举,求全排列,每次求出来之后判断是否合法,预计得分二十分
还有一种七十分的状压DP解法
我们设\(f[i][j]\)为当前排好队的人的状态为\(i\),并且队伍末尾的人为\(j\)时的方案数
所以有\(f[i][j]+=f[i^(1<<(j-1))][k];\)
其中\(abs(a[j]-a[k])%m!=0\)
\(i&(1<<(j-1))!=0\)
\(i&(1<<(k-1))!=0\)
20分暴力
#include
using namespace std;
typedef long long ll;
const ll mod=1234567891;
const int maxn=35;
ll a[maxn];
int main(){
int n;
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%lld",&a[i]);
}
ll m;
scanf("%lld",&m);
sort(a+1,a+1+n);
ll ans=0;
while(1){
bool jud=0;
for(int i=1;i 70分状压
#include
using namespace std;
typedef long long ll;
const int maxn=23;
const ll mod=1234567891;
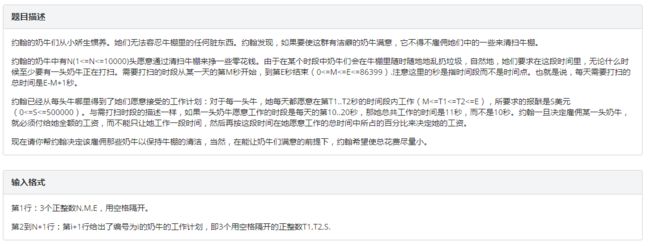
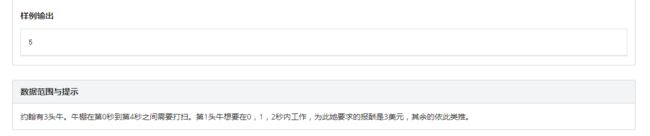
ll f[1< D、清理牛棚
分析
这道题的解法很多,有线性DP、线段树优化DP、单调栈优化DP、最短路
最短路解法
#include
using namespace std;
typedef long long ll;
const int maxn=2e6+5;
struct asd{
int from,to,next;
ll val;
}b[maxn];
int head[maxn],tot=1;
void ad(int aa,int bb,ll cc){
b[tot].from=aa;
b[tot].to=bb;
b[tot].val=cc;
b[tot].next=head[aa];
head[aa]=tot++;
}
struct jie{
int num;
ll jl;
jie(int aa=0,ll bb=0){
num=aa,jl=bb;
}
bool operator < (const jie& A) const{
return jl>A.jl;
}
};
ll dis[maxn];
bool vis[maxn];
priority_queue q;
void dij(int xx){
memset(dis,0x3f,sizeof(dis));
dis[xx]=0;
q.push(jie(xx,0));
while(!q.empty()){
int now=q.top().num;
q.pop();
if(vis[now]) continue;
vis[now]=1;
for(int i=head[now];i!=-1;i=b[i].next){
int u=b[i].to;
if(dis[u]>dis[now]+b[i].val){
dis[u]=dis[now]+b[i].val;
q.push(jie(u,dis[u]));
}
}
}
}
int main(){
memset(head,-1,sizeof(head));
int n,m,e;
scanf("%d%d%d",&n,&m,&e);
for(int i=1;i<=n;i++){
int aa,bb;
ll cc;
scanf("%d%d%lld",&aa,&bb,&cc);
ad(aa,bb+1,cc);
}
for(int i=m;i 线性DP解法
#include
using namespace std;
typedef long long ll;
const int maxn=100005;
ll f[maxn];
struct asd{
int l,r;
ll hd;
}b[maxn];
bool cmp(asd aa,asd bb){
if(aa.r==bb.r) return aa.l=e) ans=min(ans,f[b[i].r]);
}
if(ans==0x3f3f3f3f3f3f3f3f) printf("-1\n");
else printf("%d\n",ans);
return 0;
}
线段树优化DP
#include
#include
#include
using namespace std;
#define ll long long
const int maxe=9e4+1;
const int maxn=1e4+1;
const ll inf=0x3f3f3f3f3f3f3f3f;
struct Node
{
int x,y,val;
}a[maxn];
ll mn[maxe<<2];
void dfs(int x,int l,int r,int pos,ll val)
{
if(l==r)
{
mn[x]=min(mn[x],val);
return;
}
int mid=l+r>>1;
if(pos<=mid) dfs(x<<1,l,mid,pos,val);
else dfs(x<<1|1,mid+1,r,pos,val);
mn[x]=min(mn[x<<1],mn[x<<1|1]);
}
ll query(int x,int l,int r,int left,int right)
{
if(l>=left&&r<=right) return mn[x];
int mid=l+r>>1;
ll ans=inf;
if(left<=mid) ans=min(ans,query(x<<1,l,mid,left,right));
if(right>mid) ans=min(ans,query(x<<1|1,mid+1,r,left,right));
return ans;
}
int cmp(const Node &x,const Node &y)
{
return x.y