R语言 - 逻辑回归
>
library(
ggplot2)
#设置随机种子为1
>
set.seed(
1)
#将整数1,2,3分别定义为变量b0,b1,b2
>
b0 <-
1 ;
b1 <-
2 ;
b2 <-
3
#产生1000个服从正态分布的随机数分别定义为变量x1,x2
>
x1 <-
rnorm(
1000) ;
x2 <-
rnorm(
1000)
#将以上产生的b0,b1,b2,x1,x2计算定义为浮点数变量z
>
z <-
b0 +
b1*
x1 +
b2*
x2
#将z带入逻辑回归计算函数,定义为变量pr
>
pr <-
1/(
1+
exp(-
z))
#使用模拟产生二项分布数据函数rbinom,定义样本容量为1000,点分布的试验次数为1,点分布成功概率为pr “0
>
y <-
rbinom(
1000,
1,
pr)
#将x1,x2,y=factor(y)定义为数据帧变量plotdata
>
plotdata <-
data.frame(
x1,
x2,
y=
factor(
y))
#观察plotdata2全貌
>
summary(
plotdata)
#将数据帧plotdata2作可视化,定义为变量p
>
p <-
ggplot(
data=
plotdata,
aes(
x=
x1,
y=
x2,
color=
y))+
geom_point()
>
p
#将变量x1,x2,y组成数据帧带入变量data
>
data <-
data.frame(
x1,
x2,
y)
#用逻辑回归函数glm()将数据帧data进行逻辑回归分析,分析结果定义为变量model
>
model <-
glm(
y
~.,
data=
data,
family =
"binomial")
#观察分析结果model全貌
>
summary(
model)
Call
:
glm(
formula =
y
~ .,
family =
"binomial",
data =
data)
Deviance
Residuals
:
Min
1Q
Median
3Q
Max
-
2.78286 -
0.38847
0.08272
0.44502
2.36265
Coefficients
:
Estimate
Std.
Error
z
value
Pr(>|
z|)
(
Intercept)
0.9613
0.1128
8.524 <
2e-16 ***
x1
1.7954
0.1446
12.421 <
2e-16 ***
x2
2.9446
0.1973
14.926 <
2e-16 ***
---
Signif.
codes
:
0 ‘***’
0.001 ‘**’
0.01 ‘*’
0.05 ‘.’
0.1 ‘ ’
1
(
Dispersion
parameter
for
binomial
family
taken
to
be
1)
Null
deviance
:
1352.99
on
999
degrees
of
freedom
Residual
deviance
:
623.34
on
997
degrees
of
freedom
AIC
:
629.34
Number
of
Fisher
Scoring
iterations
:
6
#将模型参数定义为变量w
>
w <-
model
$
coef
#将-w[1]/w[3]作为分割线的纵截距定义为变量inter
>
inter <- -
w[
1]/
w[
3]
#将-w[2]/w[3]作为分割线的斜率定义为变量slope
>
slope <- -
w[
2]/
w[
3]
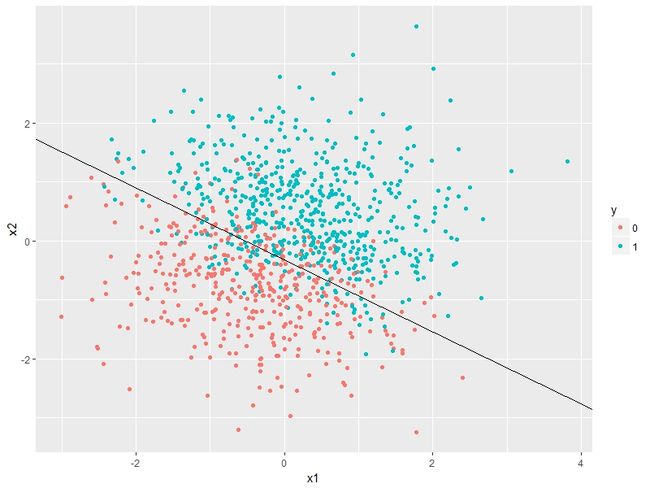
#将变量data内的数据点,和求出的分割线可视化并定义为变量p3
>
p2 <-
ggplot(
data=
plotdata,
aes(
x=
x1,
y=
x2,
color=
y))+
geom_point()+
geom_abline(
intercept =
inter,
slope =
slope)
>
p2