LeetCode#95 不同的二叉搜索树II Java

@author: sdubrz
@date: 2020.04.25
题号： 95
题目难度： 中等
考察内容： 动态规划，二叉搜索树
原题链接 https://leetcode-cn.com/problems/unique-binary-search-trees-ii/
题目的著作权归领扣网络所有，商业转载请联系官方授权，非商业转载请注明出处。
解题代码转载请联系 lwyz521604#163.com

给定一个整数 n，生成所有由 1 … n 为节点所组成的二叉搜索树。

示例:

输入: 3
输出:
[
  [1,null,3,2],
  [3,2,null,1],
  [3,1,null,null,2],
  [2,1,3],
  [1,null,2,null,3]
]
解释:
以上的输出对应以下 5 种不同结构的二叉搜索树：

   1         3     3      2      1
    \       /     /      / \      \
     3     2     1      1   3      2
    /     /       \                 \
   2     1         2                 3

通过次数28,041 提交次数44,898

我的动态规划解法

这道题是第96题的延伸。要求不仅输出二叉搜索树的个数，还要输出所有的二叉搜索树。继续沿用第96题的思路，可以使用动态规划的思想的来求解这道题。对于 1…n 为节点组成的以 x 为根节点组成的二叉搜索树，其左子树是由 1…x-1 组成的，右子树为 x+1…n 组成的。问题就变成了求左子树和右子树的所有可能。要求解整个问题，我们需要知道所有的以 i…j 为节点构成的所有二叉搜索树的可能。

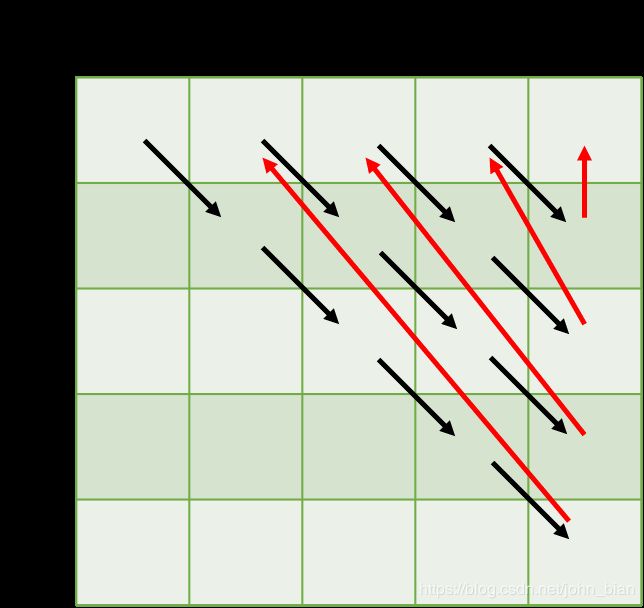
对此，我们可以构造一个表格来进行记录。如下图所示的二维数组，每个元素是一个链表。其中，第 i 行，第 j 列的链表表示的是以 i…j 为节点所构成的所有不同的二叉搜索树。我们可以按照图中箭头所示的方向完成填表，最终返回第 1 行第 n 列的链表。

下面是这一思路的Java程序实现

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
 import java.util.*;
class Solution {
    public List generateTrees(int n) {
		if(n==0) {
			List list = new LinkedList<>();
			return list;
		}
        List[][] counts = new LinkedList[n+1][n+1]; 
        List list0 = new LinkedList<>();
        counts[0][0] = list0;
        for(int i=1; i<=n; i++) {
        	List list = new LinkedList<>();
        	list.add(new TreeNode(i));
        	counts[i][i] = list;
        	counts[i][i-1] = list0;
        }
        
        for(int j=1; j<=n-1; j++) {
        	for(int i=1; i<=n; i++) {
        		if(i+j>n) {
        			break;
        		}
        		List list = new LinkedList<>();
        		for(int root=i; root<=i+j; root++) {
        			List list1 = new LinkedList<>();  // 左子树的所有可能
        			List list2 = new LinkedList<>();  // 右子树的所有可能
        			if(root>1) {
        				list1 = counts[i][root-1];
        			}  			
        			if(root iter = list2.iterator();
        				while(iter.hasNext()) {
        					TreeNode node = new TreeNode(root);
        					node.right = iter.next();
        					list.add(node);
        				}
        			}
        			else if(list2.isEmpty()) {
        				Iterator iter = list1.iterator();
        				while(iter.hasNext()) {
        					TreeNode node = new TreeNode(root);
        					node.left = iter.next();
        					list.add(node);
        				}
        			}else {
        				Iterator iter1 = list1.iterator();
        				while(iter1.hasNext()) {
        					TreeNode leftChild = iter1.next();
        					Iterator iter2 = list2.iterator();
        					while(iter2.hasNext()) {
        						TreeNode node = new TreeNode(root);
        						node.left = leftChild;
        						node.right = iter2.next();
        						list.add(node);
        					}
        				}
        			}
        		}
        		
        		counts[i][i+j] = list;
        	}
        }
        
        return counts[1][n];
    }
}

在 LeetCode 系统中提交的结果为

执行结果： 通过 显示详情
执行用时 : 2 ms, 在所有 Java 提交中击败了 74.17% 的用户
内存消耗 : 39.6 MB, 在所有 Java 提交中击败了 14.29% 的用户

官方给出的递归方法

官方给出的题解中说二叉搜索树的数量叫做卡特兰数。

官方给出的递归解法的基本思想与我前面说的思路是一致的，也是基于根节点为 x 时，左子树与右子树的可能给出的。不过官方用了递归的代码实现方式。下面是其具体的代码实现

class Solution {
  public LinkedList generate_trees(int start, int end) {
    LinkedList all_trees = new LinkedList();
    if (start > end) {
      all_trees.add(null);
      return all_trees;
    }

    // pick up a root
    for (int i = start; i <= end; i++) {
      // all possible left subtrees if i is choosen to be a root
      LinkedList left_trees = generate_trees(start, i - 1);

      // all possible right subtrees if i is choosen to be a root
      LinkedList right_trees = generate_trees(i + 1, end);

      // connect left and right trees to the root i
      for (TreeNode l : left_trees) {
        for (TreeNode r : right_trees) {
          TreeNode current_tree = new TreeNode(i);
          current_tree.left = l;
          current_tree.right = r;
          all_trees.add(current_tree);
        }
      }
    }
    return all_trees;
  }

  public List generateTrees(int n) {
    if (n == 0) {
      return new LinkedList();
    }
    return generate_trees(1, n);
  }
}

官方的代码在系统中提交的结果与前面我写的动态规划解法几乎相同，官方题解中说它的时间复杂度和空间复杂度均为 $O(\frac{4^n}{n^{1/2}})$。动态规划方法的复杂度我没有去仔细去推导，太懒了……

执行结果： 通过 显示详情
执行用时 : 2 ms, 在所有 Java 提交中击败了 74.17% 的用户
内存消耗 : 40.4 MB, 在所有 Java 提交中击败了 14.29% 的用户

本文是在 LeetCode 刷题的笔记，如有不足之处，欢迎通过留言或QQ
赐教。