AtCoder题解——Beginner Contest 168——C - : (Colon)
题目相关
题目链接
AtCoder Beginner Contest 168 C题，https://atcoder.jp/contests/abc168/tasks/abc168_c。
Problem Statement
Consider an analog clock whose hour and minute hands are A and B centimeters long, respectively.
An endpoint of the hour hand and an endpoint of the minute hand are fixed at the same point, around which each hand rotates clockwise at constant angular velocity. It takes the hour and minute hands 12 hours and 1 hour to make one full rotation, respectively.
At 0 o'clock, the two hands overlap each other. H hours and M minutes later, what is the distance in centimeters between the unfixed endpoints of the hands?
Input
Input is given from Standard Input in the following format:
A B H MOutput
Print the answer without units. Your output will be accepted when its absolute or relative error from the correct value is at most 10^−9.
Samples1
Sample Input 1
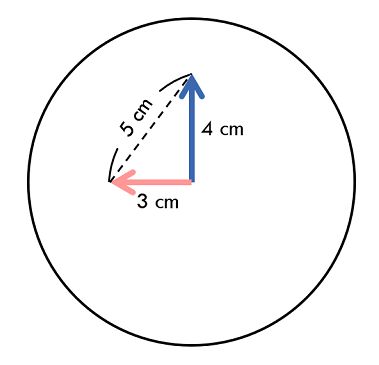
3 4 9 0Sample Output 1
5.00000000000000000000
Explaination
The two hands will be in the positions shown in the figure below, so the answer is 5 centimeters.
Sample Input 2
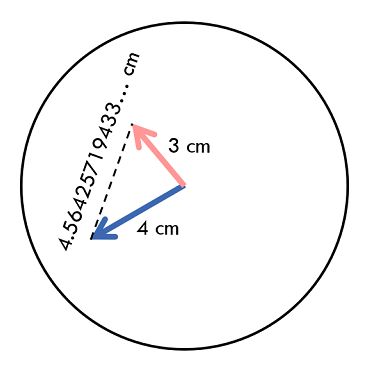
3 4 10 40Sample Output 2
4.56425719433005567605
Explaination
The two hands will be in the positions shown in the figure below. Note that each hand always rotates at constant angular velocity.
Constraints
- All values in input are integers.
- 1 ≤ A, B ≤ 1000
- 0 ≤ H ≤ 11
- 0 ≤ M ≤ 59
题解报告
本题含义
有一个模拟表，告诉我们当前的时间（包括小时和分钟），时针臂长和分针臂长，要求计算构成的三角形第三条边的长度。模拟表盘的样子是这样的，一般有三个针，时针、分针和秒针。
因此，本题是一个纯粹的数学题，给出三角形的两条边长度，求解第三条边的长度，那么本题需要使用余弦定理。
数学知识
余弦定理
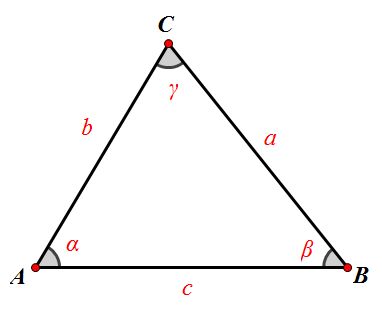
如上图所示，我们已经知道 a 和 b 的长度，只需要求出 a 与 b 之间的夹角 
即可。那么对应的 c 的长度为 
。
时针和分针角度计算
这是一个数学题目，初中数学中的钟表问题知识点。求解描述如下：
（1）普通钟表相当于圆，其时针或分针走一圈均相当于走过 360° 角；
（2）钟表上的每一个大格（时针的一小时或分针的 5 分钟）对应的角度是：
；
（3）时针每走过 1 格对应的角度应为：
；
（4）分针每走过 1 格对应的角度应为：
。
我们应该以时针、分针均在 12 点时为起始点进行计算。由于分针在时针前面，我们可以先算出分针走过的角度，再减去时针走过的角度，即可求出时针与分针夹角的度数。
假设分的数据为 M，那么对应分针走过的角度记为 
，对应的计算公式为：
。
假设小时的数据为 H，俺么对应时针走过的角度记为 
，对应的计算公式为：
。
两针的角度差为：
。
数据范围分析
本题数据范围非常小，用 int 来表示足够。
注意 int 和 double 之间的数据转换。
样例数据分析
我们忽略余弦定理的计算过程。
样例数据1
分钟的数据为 0，因此角度为 
。小时的数据为 9，因此时针角度为 
。因此两针的角度差为 
。
样例数据2
分钟的数据为 40，因此角度为 
。小时的数据为 10，因此时针角度为 
。因此两针的角度差为 
。
代码细节
1、数据类型的强制转换。
2、数据精度。题目指出超过 
都算正确，因此我们可以考虑大一个数量级。
3、C++中的三角函数相关公式的单位是弧度，不是角度。因此我们需要将角度换算成弧度。
4、弧度计算中 PI 的定义。推荐使用 acos(-1)，主要是为了保证精度。
AC 参考代码
#include
using namespace std;
int main() {
int a,b,h,m;
scanf("%d%d%d%d", &a, &b, &h, &m);
//求时钟的角度
double x1=h*30+m*0.5;
//求分钟的角度
double x2=m*6;
//求夹角
double xita = fabs(x1-x2);
if (xita>180) {
xita = 360-xita;
}
double ans = sqrt(a*a+b*b-2*a*b*cos(xita*acos(-1.0)/180));
printf("%.20lf\n",ans);
return 0;
}