AtCoder题解——Beginner Contest 170——F - Pond Skater

题目相关

题目链接

AtCoder Beginner Contest 170 F题，https://atcoder.jp/contests/abc170/tasks/abc170_f。

Problem Statement

Snuke, a water strider, lives in a rectangular pond that can be seen as a grid with H east-west rows and W north-south columns. Let (i,j) be the square at the i-th row from the north and j-th column from the west.

Some of the squares have a lotus leaf on it and cannot be entered. The square (i,j) has a lotus leaf on it if cij is @, and it does not if cij is ..

In one stroke, Snuke can move between 1 and K squares (inclusive) toward one of the four directions: north, east, south, and west. The move may not pass through a square with a lotus leaf. Moving to such a square or out of the pond is also forbidden.

Find the minimum number of strokes Snuke takes to travel from the square (x1,y1) to (x2,y2). If the travel from (x1,y1) to (x2,y2) is impossible, point out that fact.

Input

Input is given from Standard Input in the following format:

H W K
x1 y1 x2 y2
c1,1 c1,2 .. c1,W
c2,1 c2,2 .. c2,W
.
.
cH,1 cH,2 .. cH,W

Output

Print the minimum number of strokes Snuke takes to travel from the square (x1,y1) to (x2,y2), or print -1 if the travel is impossible.

Samples1

Sample Input 1

3 5 2
3 2 3 4
.....
.@..@
..@..

Sample Output 1

5

Explaination

Initially, Snuke is at the square (3,2). He can reach the square (3,4) by making five strokes as follows:

• From (3,2), go west one square to (3,1).

• From (3,1), go north two squares to (1,1).

• From (1,1), go east two squares to (1,3).

• From (1,3), go east one square to (1,4).

• From (1,4), go south two squares to (3,4).

Samples2

Sample Input 2

1 6 4
1 1 1 6
......

Sample Output 2

2

Samples3

Sample Input 3

3 3 1
2 1 2 3
.@.
.@.
.@.

Sample Output 3

-1

Constraints

• 1 ≤ H, W, K ≤10^6
• H×W ≤ 10^6
• 1 ≤ x1, x2 ≤ H
• 1 ≤ y1, y2 ≤ W
• x1 ≠ x2 or y1≠y2.
• ci,j is . or @.
• cx1,y1= .
• cx2,y2= .
• All numbers in input are integers.

题解报告

题目翻译

Snuke，水上平衡车，住在一个矩形池塘，可以看成 H 列 W 行，(i, j) 表示第 i 列第 j 行。池塘里长着荷叶，荷叶是不能进入的。如果 cij 是 @，表示荷叶。如果 cij 是 .，表示不是荷叶。

Snuke 每次可以向北、东、南、西的任意同一个方向移动一步到 K 步，但是不能通过荷叶，同时也不能移动到池塘外。

给我们起点坐标 (x1, y1) 和终点坐标 (x2, y2)，要求我们找到最小的移动步数。如果不能到达，输出 -1。

好吧。写到这里，熟悉的 BFS 模板题。和标准的 BFS 不同的地方在于，标准 BFS 一次走一格，而本题一次可以走 1~K 以内的任意格。

样例数据分析

样例数据 1

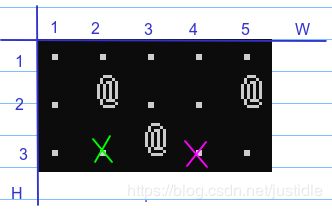
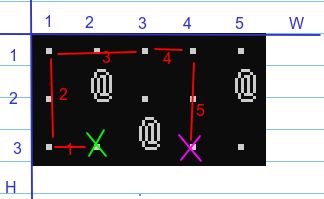
根据样例数据，H=3，W=5，K=2，表示有 3 列 5 行，每次最多走 2 步。

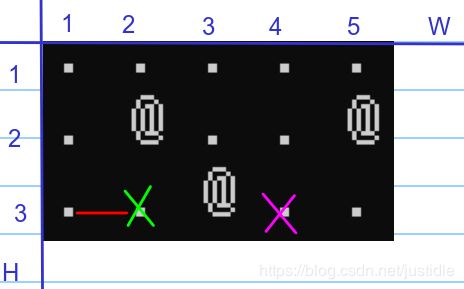
开始坐标为 (3,2)，表示第 3 列第 2 行。目标坐标为 (3,4)，表示第 3 列第 4 行。地形图如下，绿色表示起点位置，淡红色表示终点位置。

如上图所示的地图，我们可以快速绘制出如下所示的最短步骤。如下图所示。

也就是，(3,2) -> (3,1) -> (1,1) -> (1,3) -> (1,4) -> (3,4)。

样例数据 2

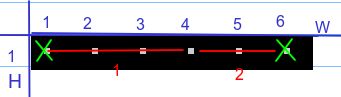
根据样例数据，H=1，W=6，K=4，表示有 6 列 1 行，每次最多走 4 步。

开始坐标为 (1,1)，表示第 1 列第 1 行。目标坐标为 (1,6)，表示第 1 列第 6 行。地形图如下，绿色表示起点位置，淡红色表示终点位置。

如上图所示的地图，我们可以快速绘制出如下所示的最短步骤。如下图所示。

也就是，(1,1) -> (1,4) -> (1,6)。

样例数据 3

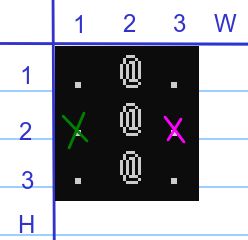
根据样例数据，H=3，W=3，K=1，表示有 3 列 3 行，每次最多走 1 步。

开始坐标为 (2,1)，表示第 2 列第 1 行。目标坐标为 (2,3)，表示第 2 列第 3 行。地形图如下，绿色表示起点位置，淡红色表示终点位置。

如上所示，我们很清楚知道，这是不可能完成的任务，因此输出答案为 -1。

题目分析

一个标准的 BFS 问题，唯一的变化是每次可以走 K 步。

剩下的问题，套用 BFS 模板即可。

数据规模分析

略。

算法设计

套用 BFS 模板。略。

可见性控制

由于每次可以走 1 ~ K 步，因此不使用标准 BFS 的 vis 属性来控制是否走到，而是使用当前点到起点的距离来控制，也就是当某个方法走到某点 (nx, ny) 后，如果新的 dis[nx][ny] 比老的 dis[nx][ny] 小，说明是一个更好走法，更新 dis[nx][ny] 即可。具体参考 AC 代码。 

下面我们用样例 1 的数据来说明一下 dis[nx][ny]的变化。

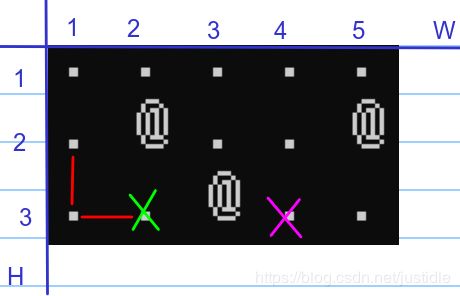
1、开始的位置是 (2, 1)，自然 dis[2][1]=0。注意我们的数组是从 0 开始的。如下图所示。

2、点 (2, 1) 出发我们只能向左，而且只能走一格。对应的新坐标为 (2,0)，那么 nd=1，对应 dis[2][0]=INT_MAX，因此设置 dis[2][0]=1。如下图所示。

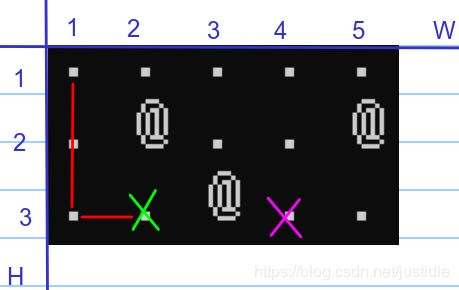
3、点 (2, 0) 出发只能向上走，先走一格。对应的新坐标为 (1, 0)，那么 nd=2（从上一个位置计算过来的），对应 dis[1][0]=INT_MAX，因此设置 dis[1][0]=2，表示从起点 (2, 1) 走 2 次到达这里。如下图所示。

4、点 (2, 0) 出发只能向上走，先走两格。对应的新坐标为 (0, 0)，那么 nd=2（从上一个位置计算过来的），对应 dis[0][0]=INT_MAX，因此设置 dis[0][0]=2，表示从起点 (2, 1) 走 2 次到达这里。如下图所示。

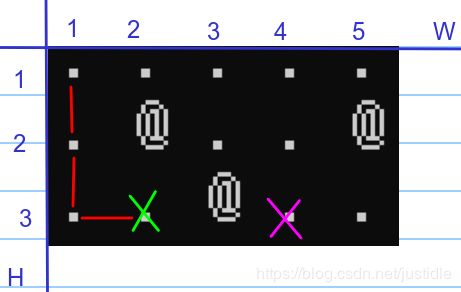
5、点 (1, 0) 出发只能向上走，先走一格。对应的新坐标为 (0, 0)，那么 nd=3（从上一个位置计算过来的），对应 dis[0][0]=2，比 nd 小，说明到 (1, 0) 点有更好的方案。没有必要更新 dis[0][0] 到起点的距离。如下图所示。

这样，我们发现通过控制 dis 的数据，解决了多种路径计算问题。后面的 BFS 过程，我们就不再继续说明。

AC 参考代码

#include 
using namespace std;

int main() {
	//读入数据
	int h, w, k;
	scanf("%d%d%d", &h, &w, &k);
	int x1, y1, x2, y2;
	scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
	//迷宫描述
	char maze[h][w];
	//距离描述
	int dis[h][w];
	for (int i=0; i > q;
	//插入起点
	dis[x1][y1] = 0;
	q.push({x1, y1});
	while (!q.empty()) {
		//获取队首数据
		int x = q.front().first;
		int y = q.front().second;
		q.pop();

		//按照规定方向移动
		for (int i=0; i<4; i++) {
			//新坐标和距离 
			int nx = x;
			int ny = y;
			int nd = dis[x][y]+1;
			//1 ~ k步
			for (int j=1; j<=k; j++) {
				//计算新的坐标
				nx += dir[i][0];
				ny += dir[i][1];

				//合法性判断
				if (nx<0 || nx>=h || ny<0 || ny>=w || '@'==maze[nx][ny] || dis[nx][ny]nd) {
					dis[nx][ny] = nd;
					q.push({nx, ny});
				}
			}
		}
	}

	int ans = dis[x2][y2];
	printf("%d\n", (INT_MAX==ans ? -1 : ans));

	return 0;
}

P.S.

难道是我碰到的最简单的 F 题。