numpy.outer、numpy.hanning、numpy.unravel_index学习总结
np.outer、np.hanning、np.unravel_index学习总结
- 1、numpy.unravel_index()
- 2、numpy.outer()
- 3、numpy.hanning()
最近看代码,又看到一些大神使用的numpy的新方法,在这里又总结总结,估计慢慢看下去,numpy是可以熟练掌握的(其实另外一个想掌握的就是pandas),废话并不多说
放一个查询官网: https://numpy.org/devdocs/index.html
1、numpy.unravel_index()
这个函数真的不太常见,但是看过例子就知道了,unravel就是拆开,阐明的意思,连起来就是“拆开的索引”。
numpy.unravel_index(indices, shape, order=‘C’)
- indices:是个整型数组(假设为A),里面的元素都是索引,是具有
shape的数组B拉平后的索引,这个拉平flatten有逐行拉伸开的(对应order=‘C’,默认),也有按列从左到右拉伸开的(对应order=‘F’),*可以看完下面例子再回过来品味* - shape:整型元组,代表数组B的shape
- unraveled_coords:返回值是一个ndarray构成的元组,元素个数=indices元素个数,是一个坐标
>>> import numpy as np
>>> xx = np.random.randn(3, 4)
>>>> xx
array([[-1.26992094, 1.53123906, 0.30685343, -1.11830275],
[-0.01614887, -1.65227584, -1.13451848, 1.31552904],
[-0.59878739, 0.00169001, -0.29459984, -0.36798817]])
>>> xx.argmax()
1
# 1就是xx逐行从上到下拉开后最大值的索引(0-based)
>>> np.unravel_index(1, (3,4))
(0, 1)
# 如果在shape为(3,4)的数组按行拉平后,索引为1的元素,正常其位置索引就是(0, 1)
>>> np.unravel_index(1, (3,4),order='F')
(1, 0)
# 如果在shape为(3,4)的数组按列拉平后,索引为1的元素,正常其位置索引就是(1, 0)
2、numpy.outer()
numpy.outer(a, b, out=None)
- a,b:都是输入的向量,假设a = [a0, a1, …, aM]和b = [b0, b1, …, bN],那么输出数组为:
out[i, j] = a[i] * b[j]
[ a 0 ∗ b 0 a 0 ∗ b 1 . . . a 0 ∗ b N a 1 ∗ b 0 . . . . . a M ∗ b 0 a M ∗ b N ] \begin{gathered} \begin{bmatrix} a0*b0 & a0*b1 & ... & a0*bN \\ a1*b0 & . & & \\ ... & & . & \\ aM*b0 & & & aM*bN\end{bmatrix} \end{gathered} ⎣⎢⎢⎡a0∗b0a1∗b0...aM∗b0a0∗b1.....a0∗bNaM∗bN⎦⎥⎥⎤
>>> im = np.outer(1j*np.linspace(2, -2, 5), np.ones((5,)))
>>> im
array([[0.+2.j, 0.+2.j, 0.+2.j, 0.+2.j, 0.+2.j],
[0.+1.j, 0.+1.j, 0.+1.j, 0.+1.j, 0.+1.j],
[0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j],
[0.-1.j, 0.-1.j, 0.-1.j, 0.-1.j, 0.-1.j],
[0.-2.j, 0.-2.j, 0.-2.j, 0.-2.j, 0.-2.j]])
>>> x = np.array(['a', 'b', 'c'], dtype=object)
>>> np.outer(x, [1, 2, 3])
array([['a', 'aa', 'aaa'],
['b', 'bb', 'bbb'],
['c', 'cc', 'ccc']], dtype=object)
3、numpy.hanning()
numpy.hanning(M)
汉宁窗是通过使用加权余弦形成的锥形
- M:整数,输出窗口中的点数。如果为零或更小,则返回一个空数组
- out:返回一个汉宁窗口,形状为(M,),最大值归一化为1(只有M为奇数时才出现该值),由下列公式计算得到:
w ( n ) = 0.5 − 0.5 cos ( 2 π n M − 1 ) 0 ≤ n ≤ M − 1 w(n)=0.5-0.5 \cos \left(\frac{2 \pi n}{M-1}\right) \quad 0 \leq n \leq M-1 w(n)=0.5−0.5cos(M−12πn)0≤n≤M−1
>>> np.hanning(11)
array([0. , 0.0954915, 0.3454915, 0.6545085, 0.9045085, 1. ,
0.9045085, 0.6545085, 0.3454915, 0.0954915, 0. ])
# 以下来自官网例子:
>>> import matplotlib.pyplot as plt
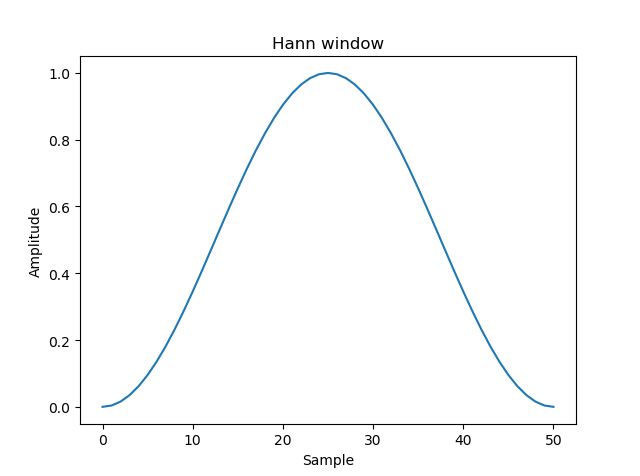
>>> window = np.hanning(51)
>>> plt.plot(window)
[<matplotlib.lines.Line2D object at 0x00000286BF8FC128>]
>>> plt.title("Hann window")
Text(0.5,1,'Hann window')
>>> plt.ylabel("Amplitude")
Text(0,0.5,'Amplitude')
>>> plt.xlabel("Sample")
Text(0.5,0,'Sample')
>>> plt.show()