【机器学习算法】基于R语言的多元线性回归分析

多元线性回归的适用条件：

（1）自变量对应变量的变化具有显著影响

（2）自变量与应变量间的线性相关必须是真实的，而非形式上的

（3）自变量之间需有一定的互斥性

（4）应具有完整的统计数据

训练数据：csv格式，含有19维特征

数据下载地址：http://pan.baidu.com/s/1eSx1fwe

步骤一：数据读取及预处理

从vt.csv文件中读取训练数据，从

rm(list = ls(all=TRUE))
library(car)
library(corrplot, quietly=TRUE)
library(sqldf)

## 数据读取
folder <- "file:///D:/My Documents/R/"
# 销量分3类读取
name <- "vt.csv"
namepre <- "vp.csv"
path <- paste(folder,name,sep = "");
pathpre <- paste(folder,namepre,sep = "")
# 训练集
dataset <- read.csv(path, na.strings=c(".", "NA", "", "?"), strip.white=TRUE, encoding="UTF-8")
# 预测集
datasetpre <- read.csv(pathpre, na.strings=c(".", "NA", "", "?"), strip.white=TRUE, encoding="UTF-8")
dataselect <- sqldf("select * from datasetpre")
datapre <- dataselect[2:ncol(dataselect)]

## 训练集准备
names <- attributes(dataset)$names
names
datatrain <- dataset[names[1:length(names)-1]]
datatarget <- dataset$t

步骤二：检查两两变量关系

cor <- cor(dataset,use="pairwise", method="pearson")
cor 
corrplot(cor)

从结果可以看到，自变量之间存在非常严重的共线性，不能直接作为回归参数输入

若自变量之间的线性关系超过自变量与因变量之间的线性关系，则回归模型稳定性收到破坏

步骤三：主成分分析

pca <- princomp(datatrain,cor=T)
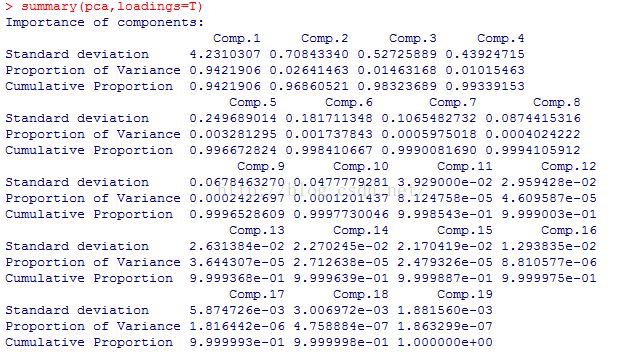
summary(pca,loadings=T)
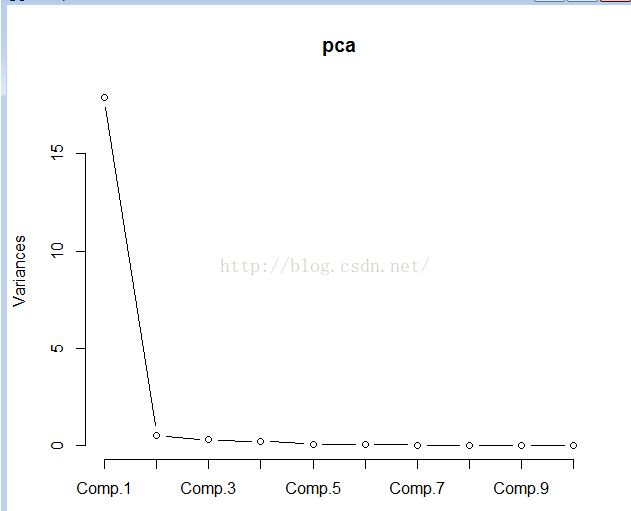
screeplot(pca,type='lines')
loading <- as.data.frame(pca$loadings[])
comps <- as.data.frame(as.matrix(datatrain)%*%as.matrix(loading))

主成分分析的碎石图

通过主成分分析，发现使用仅用2个主成分即可解释96.8%的累积误差，因此选用  comp1和comp2进行建模

步骤四：多元回归模型建立

## 主成分拟合多元线性回归方程
lmP <- lm(formula = dataset$t~comps$Comp.1+comps$Comp.2)
summary(lmP)

步骤五：模型检验

（1）拟合程度检验

R^2 为0.8905，自变量与应变量之间具有较强的线性关系

（2）估计标准误差检验

RSE值为59.48

（3）回归方程显著性检验（F检验）

F检验结果为1221，查F分布表，所有自变量与应变量的线性关系密切

（4）回归系数显著性检验（t检验）

可以看到comp1，comp2的p-value均小于0.05，表名这两个自变量对模型影响显著

（5）多重共线性检验

compsx <- comps[c("Comp.1","Comp.2")]
x <- cor(compsx,use="pairwise", method="pearson")
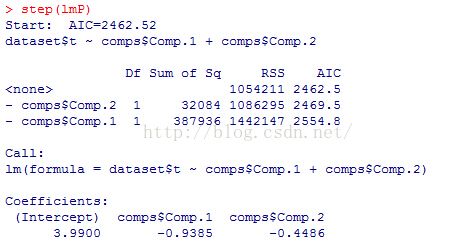
kappa(x)

step(lmP)

可以看到，kappa值等于172，仍具有较强的多重共线性（k<100，可认为不存在多重共线性）

可以利用setp函数消除多重共线性影响

步骤六：残差分析

## 残差分析
par(mfrow=c(2,2))
plot(lmP,which=1)
plot(lmP,which=2)
plot(lmP,which=3)
plot(lmP,which=4)

步骤七：模型预测及结果输出

comppre <- as.data.frame(as.matrix(datapre)%*%as.matrix(loading))[c(1,2,3)]
coe <- as.matrix(lmP$coefficients[2:length(lmP$coefficients)])
tpre <- as.matrix(comppre)%*%coe+lmP$coefficients[1]

output <- data.frame(dataselect[1],as.data.frame(tpre))
pathwrite <- paste(folder,"tpre.csv",sep = "")
write.table(output, file =pathwrite,sep =",",col.names =T,row.names = F)

将预测结果写入tpre.csv文件中

参考文献

http://blog.sina.com.cn/s/blog_8fc24da10101pfjj.html

http://blog.sina.com.cn/s/blog_6ee39c3901017fpd.html