题解 ZROI2
暑假集训的第二次模拟赛,成绩..更加惨不忍睹。又滑了rk20,(#`-_ゝ-)(sk)
链染色
考场上想出了半正解,思路上期望得分80pts,代码得分0pts,(我这辣鸡代码能力╯︿╰)实际考试的时候,由于网络波动,没能交上去,导致该题没有提交记录..(正好掩盖一下爆零的事实)
这道题在题干里就提到了并查集,再加上考前讲课的时候我听明白了,所以考场推导其实蛮顺利的
先加强一下条件,考虑一下线性情况:在一条链上有一串节点,每一次都会对指定区间内所有未染色的节点进行染色,询问所有操作之后链上节点的情况
一种显而易见的\(O(n^2)\)暴力做法是:枚举所有节点,模拟染色
这种做法的弊端是:需要大量重复访问已经被染色的节点。假如我们能够跳过被染色的节点呢?每一次只访问仍未被染色的节点,就可以在线性时间内解决问题
设 f[i] 表示区间 [i,n] 最靠左的未染色节点的坐标。初始时,f[i]=i
假如节点 i 被染色了,就将 f[i] 改成 i+1。可以发现只有一个节点 x , f[x]=x时, x 才是一个未染色的点。因此我们就顺着 f[i]不断向上跳,直到找到一个节点满足 f[x]=x
顺着f[i]不断上跳.. 抵达 f[i]=i .. !并查集
借用一下并查集的路径压缩思想,在一个跳跃的过程中,更新沿途的 f[] ,这样的话可以保证查询的效率。
红线部分即使借鉴并查集路径压缩的优化
总结一下就是:
至此,是对强化版条件的求解,我们尝试弱化回题意版本:在树上应当如何处理?
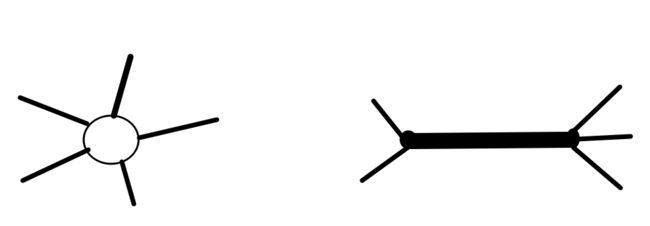
事实上,这种做法的推广比较容易实现。对于一棵树,任意节点可以有多数个子节点,但父节点总是只有一个。
然后将一条链按照LCA裂解,分别处理两条链即可
而在两条链上的情况就等同于链上的处理方法。
但是!这就ok了?观察一下数据范围:100pts n(2e6)..
LCA的预处理复杂度就在\(O(nlogn)\),数据范围好像有点不太可以接受..
发现:最后两个指针最后总会到达绿色区域上第一个未染色的节点上。!!我们并不需要事先知道LCA,两个指针不断移动的时候,判断两个指针是否相同即可(^-^)
ok,口头ac了一遍,接着代码再ac一遍:
#include
#include
#include
#include
using namespace std;
typedef long long ll;
const int MAX=2e6+5;
int n,m,ans;
int ecnt,edge[MAX],nxt[MAX],head[MAX];
int fat[MAX];
int fa[MAX][22],hei[MAX];
bool vis[MAX];
ll taru,tarv;
inline int read();
inline void insert(int,int,int);
int find(int);
void dfs(int,int);
int lca(int,int);
void calc(int,int,int);
int main(){
#ifndef ONLINE_JUDGE
freopen("test.in","r",stdin);
#endif
n=read(); m=read();
for(int i=1;i'9'){
if(tmp=='-') flag=true;
tmp=getchar();
}
while(tmp>='0'&&tmp<='9'){
sum=(sum<<1)+(sum<<3)+tmp-'0';
tmp=getchar();
}
return flag?-sum:sum;
}
void insert(int from,int to,int id){
nxt[id]=head[from]; head[from]=id; edge[id]=to;
}
int find(int p){
if(fat[p]==p) return fat[p];
else return fat[p]=find(fat[p]);
}
void dfs(int u,int faa){
fa[u][0]=faa; hei[u]=hei[faa]+1;
for(int i=1;i<=20;++i) fa[u][i]=fa[fa[u][i-1]][i-1];
for(int i=head[u];i;i=nxt[i]){
int v=edge[i]; if(v==faa) continue;
dfs(v,u);
}
}
int lca(int a,int b){
if(hei[a]=0;--i) if(hei[fa[a][i]]>=hei[b]) a=fa[a][i];
if(a==b) return a;
for(int i=20;i>=0;--i) if(fa[a][i]!=fa[b][i]) a=fa[a][i],b=fa[b][i];
return fa[a][0];
}
void calc(int a,int b,int del){
if(hei[a] 链Max
起初是一道淀粉质题,敬而远之..事实上还是一个并查集题
首先,将点权信息转换成边权信息。具体而言,对于边\(
这样处理的好处在于,一个点可能会连接四面八方的边,但一条边只有两侧的链与之相连,可以降低情况的复杂程度
依旧是考虑强化条件:将树形数据调整为链形结构
由于是对于每一条链,其最大边才会对答案产生贡献,将所有答案贡献情况枚举累加起来,即使总答案
那么就依次考虑每一条边的贡献情况:
考虑将边的权值升序排序,然后顺序添加,将其连接的两个节点的联通块连接起来,并查集的同时维护一下联通块的大小。这样枚举到当前的链时刻,两侧的节点已经被并查集维护起来,且满足并查集里节点间的边的权值均小于当前枚举边的权值。
发现有面临着一个问题:需要对并查集里所有节点快速加减
由于并查集本质上维护的是一颗树上的父子关系。如果是一颗树的话,我们就可以在子树的根上打一个标记,记作:对该子树所有节点均加减delta。
并查集的路径压缩会破坏这种树形结构,因此我们需要一种保持树形结构和高效性的合并方法:按秩合并
通过按秩合并,我们可以\(O(log n)\)处理的同时,保证树形结构。每一次合并的时候,只需要在根打上标记即可。
还有一点细节:将两个子树合并之后,大树的标记会同样的作用于小树,简单运算一下,将正确结果打上标记即可
#include
#include
#include
#include
using namespace std;
typedef long long ll;
const int MAX=2e6+5;
int n,m,ans;
int ecnt,edge[MAX],nxt[MAX],head[MAX];
int fat[MAX];
int fa[MAX][22],hei[MAX];
bool vis[MAX];
ll taru,tarv;
inline int read();
inline void insert(int,int,int);
int find(int);
void dfs(int,int);
int lca(int,int);
void calc(int,int,int);
int main(){
#ifndef ONLINE_JUDGE
freopen("test.in","r",stdin);
#endif
n=read(); m=read();
for(int i=1;i'9'){
if(tmp=='-') flag=true;
tmp=getchar();
}
while(tmp>='0'&&tmp<='9'){
sum=(sum<<1)+(sum<<3)+tmp-'0';
tmp=getchar();
}
return flag?-sum:sum;
}
void insert(int from,int to,int id){
nxt[id]=head[from]; head[from]=id; edge[id]=to;
}
int find(int p){
if(fat[p]==p) return fat[p];
else return fat[p]=find(fat[p]);
}
void dfs(int u,int faa){
fa[u][0]=faa; hei[u]=hei[faa]+1;
for(int i=1;i<=20;++i) fa[u][i]=fa[fa[u][i-1]][i-1];
for(int i=head[u];i;i=nxt[i]){
int v=edge[i]; if(v==faa) continue;
dfs(v,u);
}
}
int lca(int a,int b){
if(hei[a]=0;--i) if(hei[fa[a][i]]>=hei[b]) a=fa[a][i];
if(a==b) return a;
for(int i=20;i>=0;--i) if(fa[a][i]!=fa[b][i]) a=fa[a][i],b=fa[b][i];
return fa[a][0];
}
void calc(int a,int b,int del){
if(hei[a] 删数字
考场的时候精神分裂?c++玄学报错?总之好尿多磨..
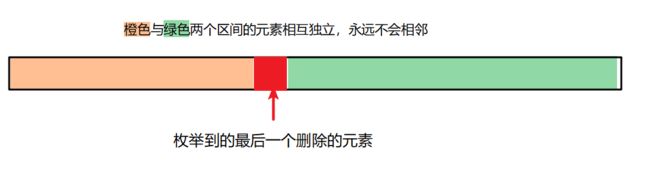
如果从头开始删数字,会有大量大量大量到无法统计的情况需要分类讨论。“因此”(套路上的因此),考虑枚举最后一个删除的元素
对于最后一个删除的元素,其左右两侧区间的所有元素都不会彼此相邻,具有相互独立的性质,可以分治解决
记左区间的方案数为\(S_l\),右区间为\(S_r\),,那么根据简单的乘法原理,得到总方案数\(S_l\times S_r \times C_{r-l}^{k-l}\),最后答案累加即可
设 f[l][r] 表示区间 [l,r] 满足条件的所有方案数,\(O(n^3)\)转移
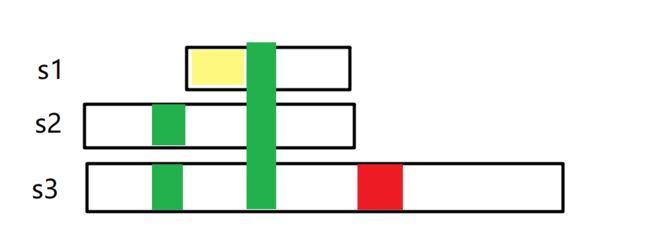
即可?好像还有一些细节欠推敲。考虑下面的这种情形
在s1中,显然绿色部分必须比黄色部分更先被删除,否则就会与s2串中的最左端绿色相邻。具体而言,对于区间 [l,r] ,不允许与 w[l-1] 和 w[r+1] 相同且相邻
这么一来,原来对于 f[l][r] 的定义似乎有些不够充分,补充如下
f[i][j] 表示区间 [l,r] 满足条件的所有方案数,且不与 w[l-1] 和 w[r+1] 相同且相邻
定义改变了,那么转移方式也必须相应的改变:当枚举到的k满足 “w[k]=w[l-1]” 或者 "w[k]=w[r+1]" 时,倘若k最后被删除,那么一定是不满足条件的;反之,只要k不是最后删除,根据定义的转移一定是满足条件
伪代码如下:
类似区间dp枚举区间 (l,r){
枚举 k 属于 (l,r) ,且 满足 (w[k]!=w[l-1]!=w[r+1]){
f[l][r]+=s_l*s_r*c(r-l)(k-l)
}
}
#include
#include
#include
#include
using namespace std;
typedef long long ll;
#define foR(a,b,c) for(a=b;a<=c;++a)
#define For(a,b,c) for(a=c;a>=b;--a)
int i,j,k;
const int MAX=555;
const ll MOD=998244353ll;
int n,a[MAX];
ll f[MAX][MAX],c[MAX][MAX];
void init();
int main(){
#ifndef ONLINE_JUDGE
freopen("test.in","r",stdin);
#endif
scanf("%d",&n);
foR(i,1,n) scanf("%d",&a[i]);
init();
a[0]=a[n+1]=-1;
For(i,1,n){
foR(j,i,n){
foR(k,i,j){
if(a[k]==a[i-1]||a[k]==a[j+1]) continue;
ll left=(k==i?1:f[i][k-1]),right=(k==j?1:f[k+1][j]);
f[i][j]+=(left*right%MOD*c[j-i][k-i]%MOD); f[i][j]%=MOD;
}
}
}
printf("%lld\n",f[1][n]);
return 0;
}
void init(){
c[0][0]=1;
foR(i,1,500) c[i][0]=c[i][i]=1;
foR(i,2,500) foR(j,1,i-1) c[i][j]=(c[i-1][j-1]+c[i-1][j])%MOD;
}
这场比赛其实的期望分数是100+60+0=160,期望排名在rk4。但是事实上实际得分10pts,连零头都不到。。总结一下还是代码能力不足。很多思想能构想出来,却缺乏依次性实现不出错的能力
(* ̄3 ̄)╭