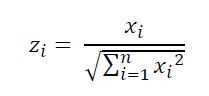数学建模方法——带权重的TOPSIS法
目录:
- topsis简介
- topsis法基本原理
- 数据正向化
2.1. 极小型指标转化为极大型指标
2.2. 中间型指标转化为极大型指标
2.3. 区间型指标转化为极大型指标- 标准化
- 评分构建
- 总结
0. topsis简介
Topsis法,全称为Technique for Order Preference by Similarity to an Ideal Solution中文常翻译为优劣解距离法,该方法能够根据现有的数据,对个体进行评价排序。Topsis法和之前讲过的AHP方法一样,都可以对一系列的个体进行评价,不过通常来说AHP的应用场景是在没有明确的量化指标的情况下,而topsis是在有量化指标的情况下完成的。
例如,我们之前的例子是说小明想要买饮料,那么如何从可乐,雪碧和汇源果汁中进行选择,这很明显大部分是基于买饮料的人的主观想法进行选择的。Topsis法应用的场景就比如在医院检查身体,医生最后会给每个人体检报告,上面有你的一些和健康相关的指数,在这种有实实在在数字支持的时候,如何较为客观的评价大家的健康状况就是我们要研究的问题。
1. topsis法基本原理
Topsis法的基本原理从他的中文名称中就可以大体知晓——优劣解距离法,那么简单的理解就是一个指标,到该指标的最优解的距离越小说明越好,举个例子,考试满分是100分,那么你考了90分,和100的距离是10分,小明考了80分,和最好的100分距离是20分,比你更远,所以从成绩上看你要比小明更接近最优的分数,所以你更好,就这么简单。当数据是多个维度的时候,比如说有好多次的成绩,有月考成绩,期中考试成绩,期末考试成绩。那么为了知道谁的分数最好,我们就可以计算在三维上,成绩到最好成绩之间的距离作为指标,距离越近说明成绩越好。比如你的成绩是(90,95,90),最好的成绩是(100,100,100)那么你到最好的成绩之间的距离就是:

这里这个距离越小,就说明你到最优点的距离越小,也就越好,基本的思想就是这样的,但是实际上还有一些小的改动。我们以下面的表格为例

我们仔细观察上面的表格,发现事情没有想象的那么简单,数据纷繁复杂大小不一,最优的值也不像考试一样有个100分的明确指标,如何综合的考虑这些指标,就是今天要解决的问题。
2. 数据正向化
有的数据是越大越好,有的数据是靠近某个值越好,有的是在一个区间中最好,这种不同的方向和区间让分析变得混乱,为了简化分析我们将数据进行正向化处理,都让他越大越好。通常来说,常见的数据可以分为四类:
- 极大型指标(效益类指标):指标数值越大越好。
- 极小型指标(成本类指标):指标数值越小越好。
- 中间型指标:指标数值越接近某个值越好。
- 区间型指标:指标数值在某个区间范围内最好,区间中的数值大小无优劣之分。
为了将其余三种指标正向化,我们可以采用如下的策略,假如一个指标的所有数据记为大写的X,其中的元素记为x_i:
2.1. 极小型指标转化为极大型指标:

其中x_i上面加一个横线,代表转化后的结果。通过这种方法,我们就可以将一个越小越好的指标转化为越大越好的指标
2.2. 中间型指标转化为极大型指标:

这里x_best指代的是最好的值,在本例子中也就是7.4,两条竖线代表绝对值符号。这里的分母求得的是偏离最好值最远的值。
2.3. 区间型指标转化为极大型指标:
这里的想法和中心型一样,先算出M,即偏离最优区间最远的值,然后通过1减去每个数据的偏离程度再除以M将区间型指标转化为极大型指标。

举个例子在这道题中,第一列肺活量是正向型指标,故不需要进行正向化处理,第二列癌变指数是越小越好的,我们可以用最大值减去当前值的方法得到正向化的结果,这样第一个值就变为0.2-0.01 = 0.19; 第二个值为0.2-0.2 = 0等。第三列是中间型指标,通过计算我们发现最大的偏差是0.4所以第一个值计算的时候用7.4-7.35 = 0.05, 再用0.05/0.4= 0.125 再用1减去0.125 等于0.875。第四列是区间型,套用2.4的公式M是最大的偏差是20,第一个值在区间范围内,置为1,第二个值小于66,用66-63 = 3,3/20=0.15 再用1减去,得到0.85。
回顾一下,这里介绍了三种常见数据的正向化方法,正向化是为了将数据都变为越大越好的数值类型,方便之后的运算。这里需要注意的是,正向化的方法并不唯一。
3. 标准化
经过了正向化后,还存在一个问题就是所有的值都有他的量纲,以经过了正向化的表格数值为例,假如直接计算距离,那么肯定是肺活量越大的人越健康,毕竟肺活量要比其他值大得多,为了消除数据量纲的影响我们需要对数据进行标准化处理。对于每一列的数据进行标准化的方法如下:
即,当前的值,除以所在列的平方和的开方,如第一列中,我们首先计算分母,用5000的平方加上4500的平方,一直加到5100的平方,之后再开方,得到约等于10325.7 进过计算便可得到以下的表格。

4. 评分构建
经过了正向化和标准化的修正之后,剩下的步骤就是进行评分指标的构建,构建的方法也很易懂,第一步是寻找各个指标的最大值和最小值,比如在肺活量中,最大的值是0.49最小是0.39; 癌变指数最大是0.59,最小是0.00; Ph值最大是0.64,最小是0.00; 甲状腺素最大是0.56,最小是0.00;联合这些不同的指标,我们就能构建一个多维的最大值的指标{0.49, 0.59, 0.64, 0.56} 和多维的最小值的点{0.39, 0.00, 0.00, 0.00},这两个集合分别被称为最优方案,和最差方案或者叫最劣方案,回顾这个topsis方法的中文名字:优劣解距离法,我们就知道最终的评分是用一个样本到最优和最劣解的距离定的,其中到最优解的距离记为D+,到最劣解的距离记为D-,最终的评价指标C就是

其中C越接近于1,就说明这个更优。最后根据C从大到小的顺序,评价各个参选人的优劣。例如,小明的C的计算方法如下:

再计算C就能得到最终的结果。这样的计算我们发现了一个问题,就是并没有加入权重系数,我们按照如上方法计算距离的时候是假定各个因素对于最终的评价都是等价的,没有重要性之分,然而实际上这是不可能的,那么用何种方法加入权重呢?
4.1 增加距离权重
增加距离权重主要有两个方法,一个就是AHP,通过构建判断矩阵并求解系数的方式得到不同因素的重要程度,假设对于四个因素的权重分别为w1,w2,w3和w4那么最后距离的表达式应该为
![]()
因为AHP的判断矩阵在这种专业问题上,最好是由专业的医生来填写,然而鉴于医生并不好找,为了相对客观的构建权重系数,我们还可以使用另一种方法,即熵权法构建系数。
熵权法构建系数利用了一定的信息论的知识,简单的说,就是数据的变异程度(方差)越大,就说明这个指标蕴含的信息量越大,也就越重要。例如,所有的检查身体的小朋友肺活量都是5000,那么这个指标的变异程度(方差)就超级小,也没对最终的判断做出贡献,所以这个指标的权重就可以赋为0。
具体的计算方式如下:首先应用到的矩阵是经过了正向化和归一化之后的矩阵,如果之后矩阵中还存在负数,则需要用其他方法再次归一化,比如说用值减去指标的最小值,再除以指标最大值和最小值的差。以保证所有的权重都是正数。
第二步计算熵值,计算方法如下:

其中p值的计算可以用相应值除以一列中数值的和,比如第一列,第一个数据概率的计算方法,就可以为0.48/(0.48+0.44+0.39+0.43+0.49)得到,n是个数,这里为5。之所以除以了一个ln(n)是为了归一化
第三步构建权重,权重的构建方法是首先用1-e得到信息的效用值,之后因为权重只和为1,在对权重进行归一化即可得到w权重。
熵权法在一些场景下并不合理,比如说在一些罕见的影响因素上就无法客观的赋予权重,例如,在健康评价表格中,有一项指标是谁曾经经历过核爆炸并且遭受了过量的核辐射,很明显绝大多数人都会填写0,即没有经受过,假如有一个人经历过填写了1,整体的数据变异性也是相当小的,因此会被分配很小的权重。然而被辐射对身体健康的影响实际上是非常大的,因此这时候使用熵权法对数据进行赋值就是很不合理的。
回顾一下,这节主要介绍了如何利用最优和最劣的距离构建评价指标,以及如何在构建距离的时候考虑不同因素的权重大小。权重的计算方法大体可以分为两种,一个是AHP,一个是熵权法。
5. 总结
从topsis算法的思想实际上还是很朴素的,可以简单的理解为通过计算点到最优点的距离和最劣点的距离去评价好坏。