机器学习——BP神经网络算法
1、背景
以人脑中的神经网络为启发，历史上出现过很多不同的版本，最著名的算法是1980年的backpropagation
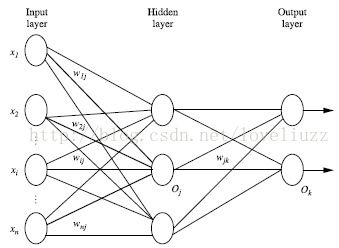
2、多层向前神经网络（Multilayer Feed-Forward Neural Network）
backpropagation被使用在多层向前神经网络上，多层向前神经网络由一下几部分组成：
输入层（input layer）、隐藏层（hidden layers）、输出层（output layer）
（1）每层由单元（unit）组成，每个单元可以被称作神经结点，根据生物学来源定义。
（2）输入层（input layer）是由训练集的实例特征向量传入，经过连接节点的权重（weight）传入下一层，
一层中的加权的求和，然后根据非线性方程转化输出一层的输出是下一层的输入。
（3）隐藏层的个数可以是任意的，输入层和输出层都有一层。
（4）上图称为2层的神经网络（输入层不算）。
（5）作为多层向前神经网络，理论上，如果有足够多的隐藏层和足够大的训练集，可以模拟任何方程。
3、设计神经网络结构
（1）使用神经网络训练数据之前，必须确定神经网络的层数，以及每层单元的个数。
（2）特征向量在被传入输入层时通常先被标准化（normalize）到0-1之间（为了加速学习过程）。
（3）离散型变量可以被编码成每一个输入单元对应一个特征值可能赋的值。（神经网络既支持离散变量也支持连续变量）
比如：特征值A可能取3个值（a0,a1,a2），可以使用3个输入单元来代表A。
如果A=a0，那么代表a0的取值单元为1，其他都为0.
如果A=a1，那么代表a1的取值单元为1，其他都为0，依此类推。
（4）神经网络既可以用来做分类（classification）问题也可以解决回归（regression）问题，分类问题预测值是离散型变量，回归问题预测值是连续型变量。
对于分类问题，如果是2类，可以用1个输出单元表示（0和1分别代表2类）。如果多于2类，每一个类别用一个输出单元表示，
所以，输出层的数量通常等于类别的数量。
（5）没有明确的规则来设计最好有多少个隐藏层，根据实验测试和误差，以及准确度来对实验进行改进。
4、交叉验证方法（Cross-Validation）
设置隐藏层的层数用准确度来判断，用科学的交叉验证方法计算出的准确度更常用。
将一份数据分成k份，第一次用第1份做测试，剩余的k-1份做训练集，计算出一个准确度；第二次用第2份做测试，剩余的k-1份做训练集，
计算出一个准确度；以此类推，计算出k个准确度，取它们的平均值作为最终的准确度，这个算法也称作k-fold cross validation。
5、Backpropagation算法
Neural Network是一种神经网络结构，Backpropagation算法使用在这种神经网络结构上面的。
（1）通过迭代性来处理训练集中实例。
（2）通过对比神经网络后输入层预测值（predicted value）与真实值（target value）之间的差距
（3）反方向（从输出层=>隐藏层=>输入层）来以最小误差（error）来更新每个连接的权重（weight）和偏向（bias）
6、算法的详细介绍
（1）输入：D：训练集 学习率（learing rate） 一个多层向前神经网络
（2）输出：一个训练好的神经网络——a trained neural network（权重全部更新好使得真实值与预测值之间的差最小化）
（3）初始化权重（weight）和偏向（bias）：随机初始化在-1到1之间或者-0.5-0.5之间，每个单元有一个偏向。
（4）对于每一个训练实例，执行以下步骤：
a:由输入层向前传入（先随机给出一些权重，输入层乘以对应权重求和再进行非线性转化）
输入层乘以对应权重求和公式为：
，Oi是前一层经过非线性转化的输出值，具体过程如下图：
非线性转化公式为：
b、根据误差（error）反向传输
对于输出层误差：
，其中，Oj是算出的预测值，Ti是原本真实的标签值
对于隐藏层误差：
，Errk是前面一层的误差（注：这里是反向传输，
举例：要求隐藏层第4个结点的误差，由于反向传输Errk作为前一层是结点6的误差）
权重更新：
，l是学习率（在0-1之间，开始设置大一点，然后逐渐减小的优化方法）
偏向更新：
c、终止条件
权重的更新低于某个阈值
预测的错误率低于某个阈值
达到预设一定的循环次数
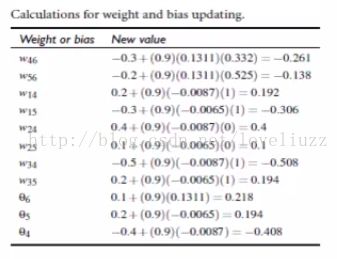
7、Backpropagation算法举例
总结：随着计算机硬件的更新和计算速度的极大提高，最近四五年里，深度学习非常火爆，
它的基本思想还是利用Backpropagation算法，只不过是多增加了几层隐藏层，使得实验结果的准确率达到很高。