机器学习笔记之R语言基础篇3（概率分布1）
接下来我们介绍概率分布
好了，接下来我们开始吧！
—-正太分布—-
概率密度函数 dnorm density
累积概率函数 pnorm probility
1.概率密度函数及累积概率函数简单回顾—
在这里，F(x)是原分布函数，即为累计概率函数，f(x)是概率密度函数
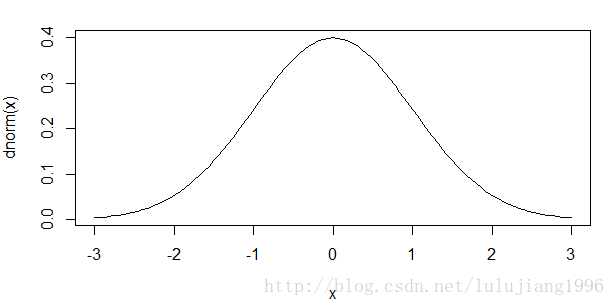
如下图，其为正太分布的概率密度函数，f(x)
曲线f(x)与x轴间所覆盖的面积即为F(X)，即为累计概率函数
2.r中的概率密度函数
#-3到3间的概率密度函数,curve为绘图函数
> curve(dnorm,from=-3,to=3)
3.R中的累计概率函数
#导入此包是为了画图，后面章节会有详细介绍
> library(ggplot2)
> x=seq(-3,3,0.01)
> z=pnorm(x)
> data=data.frame(x,z)
> ggplot(data,aes(x,z))+geom_line()
提问，为什么这里不用curve函数画图？
我们来看以下代码
> curve(dnorm(x))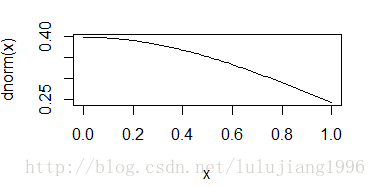
curve函数要配合输入的x范围区间才能较好显示出我们要的图形。
-回顾正太分布-
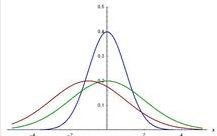
如上图，X服从正太分布，Y服从标准正太分布
上图为普通正太分布的概率密度，其中标准差越大，图像越扁，反之越高，均值为其图像的对称轴。
上图为标准正太分布的概率密度，此时均值为0，方差为1.
正太分布的面积分布—
正太曲线与x轴的某（任意）一段区间所围成的面积 表示 变量值落在该区间的概率（简单记为，其[a,b]间的面积即为[a,b]间的概率）
正太分布面积图如下：
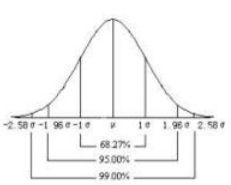
区间(μ-σ,μ+σ)内的面积为68.268949%
P{|X-μ|<σ}=2Φ(1)-1=0.6826
区间(μ-1.96σ,μ+1.96σ)内的面积为95.449974%
P{|X-μ|<2σ}=2Φ(2)-1=0.9544
区间(μ-2.58σ,μ+2.58σ)内的面积为99.730020%
P{|X-μ|<3σ}=2Φ(3)-1=0.9974
正太分位数–
分位数有三种，α分位数、上侧α分位数与双侧α分位数。
F(x)为随机变量分布函数。
当α满足0 <α<1 时
α分位数：使P{X< xα}=F(xα)=α的数 xα【面积为α时的x】
上侧α分位数：使P{X >λ}=1-F(λ)=α的数 λ【面积为1-α时的x】
双侧α分位数：使P{X<λ1}=F(λ1)=0.5α的数 λ1【面积为0.5α的x1】
使 P{X>λ2}=1-F(λ2)=0.5α的数λ2【面积为1-0.5α的x2】–分位数 qnorm quantile
#正太分布在0.5处的分位数(面积为0.5时的x值)
> qnorm(0.5,0,1)
[1] 0
#正太分布在0.975处的分位数（面积为0.975时的x值）
> qnorm(0.975,0,1)
[1] 1.959964
#以上也可写为
> qnorm(0.5)
[1] 0
> qnorm(0.975)
[1] 1.959964
–随机数 rnorm random
#rnorm(随机值个数，平均值，标准差）
> rnorm(5,0,1)
[1] -0.4755264 -0.4234262 0.4926992 -0.2733262
[5] 0.6941299练习：
z is Normal(0,1):
1.p(-1<z<=2)
2.b such that p(-b<z<=b)=0.90#F(2)-F(1),即求面积差
> pnorm(2)-pnorm(-1)
[1] 0.8185946
#F(b)-F(-b)=2F(b)=0.90，F(b)=0.45,即求面积为0.45的分位数
> qnorm(0.45)
[1] -0.1256613
好了，这一节就到这里吧，我们下节继续~