深度学习——单层感知器从原理到实践

单层感知器

首先我们从人工神经网络第一次兴起的单层感知器谈起。

1.工作原理

感知器（perceptron），有的也称其为感知机，是人工神经网络中最基础的网络结构（perceptron一般特指单层感知器，而多层感知器一般被称为MLP）。

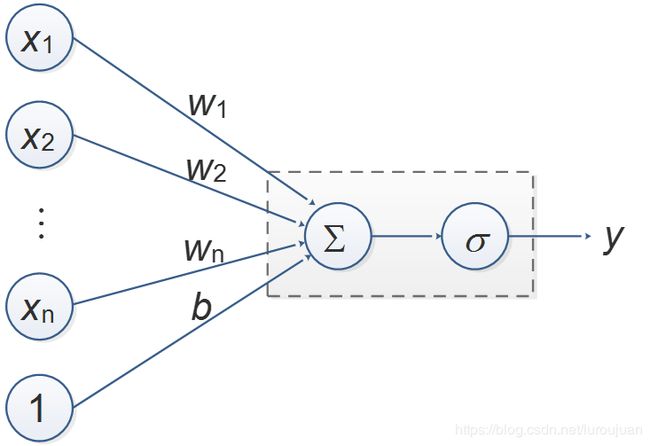
下图给出了一种单层感知器的模型，可以用公式表示为

其中X代表向量[x1,x2,…,xn,1]，W代表向量[w1,w2,…,wn,b]，σ代表激活函数。

对于一组输入值X，我们期望该网络的输出值为Y，而实际输出值为y，则我们定义损失函数（或者称为代价函数、目标函数）L为：

其中的X和Y都是已知值，可见L是关于W的函数。如果我们通过改变W，使得L等于0或者无线趋近于0，则此时可以认为网络的输出值y就等于期望值Y。那么如何更改W呢？一种方法是梯度下降法：先确定一个初始值，然后将W沿着梯度下降的方向进行调整，就会使得L的值向更小的方向进行变化。

为了更直观的理解，我们将上式中的X看做一个数3，Y也是一个数9，σ函数为y=x。则

用图像表示L与W的关系如下图

初始值W为w0=6，此时L值为40.5。而在w0处的梯度值d（导数值）为-3*(9-3w0)=27，则沿着梯度下降方向调整到w1处，w1= w0-0.1*d=3.3，将w1代入求得L为0.405。可见L的值变小了。

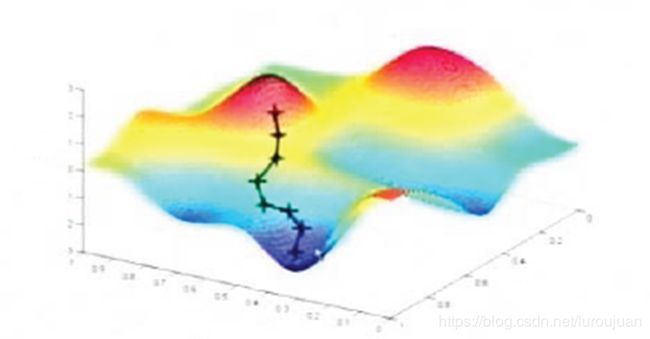
如果X包含多个数，则在多维空间中L是关于W的一个超曲面，梯度下降就是沿着梯度下降的方向调整W使得L变小，直到最小。

用公式表示梯度下降如下：

其中r代表学习率，表示沿着梯度下降方向调整的幅度，即上面调整到w1处时用到的0.1。r越大，调整的幅度越大，L变小的速度越快，但有可能导致L值越来越大或L值振荡；r越小，L的变化速度越慢，可能经过上万次的调整，L也没有达到最小值。

那么回到最开始提到的感知器模型，如何更改W呢，公式推导如下。

其中σ'为激活函数σ的导数。

如果σ函数为sigmoid函数：

则σ函数的导数为：

代入到中，则

而
 

所以当激活函数为sigmoid函数时，W的更新公式为：

2.代码实践

# coding:utf-8

import numpy as np
import matplotlib.pyplot as plt


def tanh(x):
    return np.tanh(x)


def tanhDerivate(x):
    # return 1.0 - np.tanh(x) ** 2
    return 1.0 - x ** 2

def sigmoid(x):
    return 1 / (1 + np.exp(-x))


def sigmoidDerivate(y):
    # return sigmoid(x) * (1 - sigmoid(x))
    return y * (1 - y)


class MyPerceptron:
    def __init__(self, activation='sigmoid'):
        self.W = []
        if activation == 'sigmoid':
            self.activation = sigmoid
            self.activationDerivate = sigmoidDerivate
        if activation == 'tanh':
            self.activation = sigmoid
            self.activationDerivate = sigmoidDerivate

    # 训练函数，X矩阵，每行是一个实例 ，y是每个实例对应的结果，
    # learning_rate学习率
    # epochs进行更新的最大次数
    def fit(self, X, Y, learning_rate=0.1, epochs=100):
        #将偏置项b对应的1加入到X中
        temp = np.ones([X.shape[0], X.shape[1] + 1])
        temp[:, 0:-1] = X
        X = temp
        #初始化权重W
        self.W = (np.random.random(X.shape[1]) - 0.5) * 2

        for i in range(epochs):
            y = self.activation(np.dot(X, self.W.T))
            lost = 0.5*(Y-y).dot((Y-y))
            print("第", i, "次迭代后权重", self.W, "输出结果", y, "损失",lost)
            if (y == Y).all():
                print("在第", i, "次终止")
                break
            newW = self.W + learning_rate * (((Y - y)*self.activationDerivate(y)).dot(X))
            self.W = newW

    # 绘图
    def show(self, X, Y):
        k = -self.W[0] / self.W[1]
        b = -self.W[2] / self.W[1]
        print("斜率：", k)
        print("截距：", b)
        xdata = np.linspace(0, 5)
        plt.figure()
        plt.plot(xdata, xdata * k + b, 'r')
        for i in range(X.shape[0]):
            if(1 == Y[i]):
                plt.plot(X[i][0], X[i][1], 'bo')
            else:
                plt.plot(X[i][0], X[i][1], 'yo')
        plt.show()

    # 预测函数
    def predict(self, x):
        x = np.array(x)
        temp = np.ones(x.shape[0] + 1)
        temp[0:-1] = x
        x = temp
        y = self.activation(np.dot(x, self.W.T))
        return y


def main():
    X = np.array([[0, 0], [1, 2], [2, 1], [2, 2], [3, 1],
                  [2, 4], [3, 3], [5, 1], [4, 3], [2, 6]])
    Y = np.array([0, 0, 0, 0, 0, 1, 1, 1, 1, 1])
    pt= MyPerceptron('sigmoid')
    pt.fit(X, Y, 0.1, 400)
    pt.show(X, Y)
    for i in X:
        print("输入：", i, " 输出：", pt.predict(i))


if __name__ == "__main__":
    main()

运行结果如下：

输入： [0 0]  输出： 0.030725156902869845 输入： [1 2]  输出： 0.24670252998322167 输入： [2 1]  输出： 0.22639933911778545 输入： [2 2]  输出： 0.39822509707733217 输入： [3 1]  输出： 0.37160336300393293 输入： [2 4]  输出： 0.7718721324356966 输入： [3 3]  输出： 0.75146373050736 输入： [5 1]  输出： 0.7071282498798505 输入： [4 3]  输出： 0.8593431437137449 输入： [2 6]  输出： 0.9453544041375033

如果对输出结果进一步处理，大于0.5等于1，小于0.5等于0，则预测结果与期望值完全对应。

下图表示了输入值和训练得到的分界线的关系。

另外，尝试着调整一下学习率和迭代次数，看看发生什么变化。

版权声明：本文为博主原创文章，转载请注明链接 https://blog.csdn.net/luroujuan/article/details/85225244