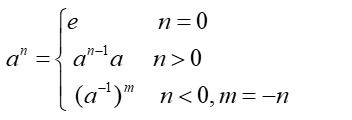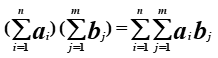离散数学-10 群与环

定义10.1

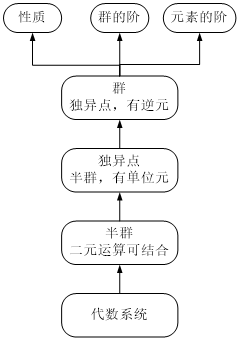
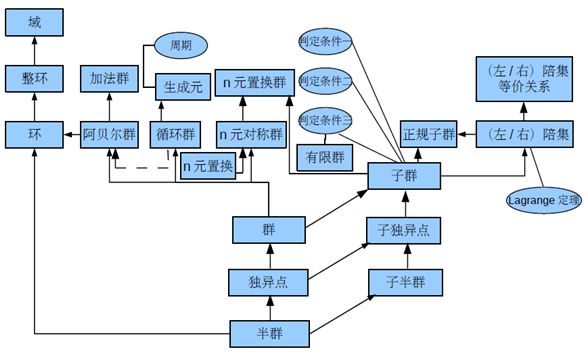
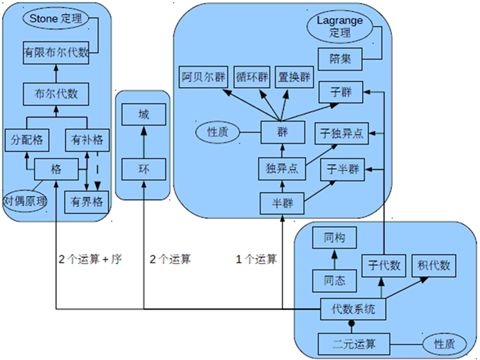
(1) 设V=<S, ∘ >是代数系统，∘为二元运算，如果∘运算是可结合的，则称V为半群.

(2) 设V=<S,∘>是半群，若e∈S是关于∘运算的单位元，则称V是含幺半群，也叫做独异点. 有时也将独异点V 记作 V=<S,∘,e>.

(3) 设V=<S,∘>是独异点，eS关于∘运算的单位元，若 aS，a^1S，则称V是群. 通常将群记作G.

定义10.2 (1) 若群G是有穷集，则称G是有限群，否则称为无限群. 群G 的基数称为群 G 的阶，有限群G的阶记作|G|.

(2) 只含单位元的群称为平凡群. 

(3) 若群G中的二元运算是可交换的，则称G为交换群或阿贝尔 (Abel) 群.

定义10.3 设G是群，a∈G，n∈Z，则a 的 n次幂.

定义10.4 设G是群，a∈G，使得等式 a^k=e 成立的最小正整数k 称为a 的阶，记作|a|=k，称 a 为 k 阶元. 若不存在这样的正整数 k，则称 a 为无限阶元.

定理10.1设G 为群，则G中的幂运算满足：

(1) a∈G，(a^1)^1=a

(2) a,b∈G，(ab)^1=b^1a^1

(3) a∈G，aⁿa^m = a^n+m，n, m∈Z

(4) a∈G，(aⁿ)^m = a^nm，n, m∈Z

(5) 若G为交换群，则 (ab)ⁿ = aⁿbⁿ.

定理10.2 G为群，a,b∈G，方程ax=b和ya=b在G中有解且仅有惟一解.

定理10.3 G为群，则G中适合消去律，即对任意a,b,c∈G 有

(1) 若 ab = ac，则 b = c.

(2) 若 ba = ca，则 b = c.

定理10.4 G为群，a∈G且 |a| = r. 设k是整数，则

(1) a^k = e当且仅当r | k

(2 )|a^1| = |a|

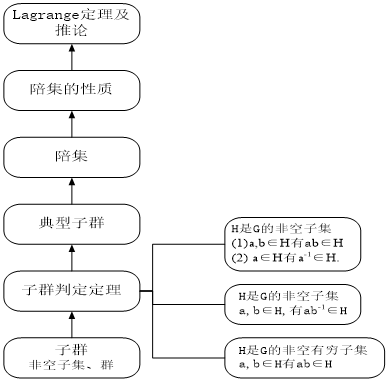
定义10.5设G是群，H是G的非空子集，

(1) 如果H关于G中的运算构成群，则称H是G的子群, 记作H≤G.

(2) 若H是G的子群，且HG，则称H是G的真子群，记作H<G.

对任何群G都存在子群. G和{e}都是G的子群，称为G的平凡子群. 

定义10.6设G为群，a∈G，令H={a^k| k∈Z}，则H是G的子群，称为由 a 生成的子群，记作<a>.

定义10.8设G为群, 令

L(G) = {H | H是G的子群}

则偏序集< L(G),  >称为G的子群格

定义10.10 设G是群，若存在a∈G使得

 G={a^k| k∈Z}

则称G是循环群，记作G=<a>，称 a 为G 的生成元. 

循环群的分类：n 阶循环群和无限循环群. 

设G=<a>是循环群，若a是n 阶元，则

G = { a⁰=e, a¹, a², … , a^n1 }

那么|G| = n，称 G 为 n 阶循环群.

若a 是无限阶元，则

G = { a⁰=e, a^±1, a^±2, … }

称 G 为无限循环群. 

定理10.13 设G=<a>是循环群. 

(1) 若G是无限循环群，则G只有两个生成元，即a和a^1. 

(2) 若G是 n 阶循环群，则G含有(n)个生成元. 对于任何小

于n且与 n 互质的数r∈{0,1,…,n-1}, a^r是G的生成元.

定理10.14 设G=<a>是循环群. 

(1) 设G=<a>是循环群，则G的子群仍是循环群.

(2) 若G=<a>是无限循环群，则G的子群除{e}以外都是无限循环群.

(3) 若G=<a>是n阶循环群，则对n的每个正因子d，G恰好含有一个d 阶子群.

定理10.5（判定定理一）

设G为群，H是G的非空子集，则H是G的子群当且仅当

(1) a,b∈H有ab∈H

(2) a∈H有a^1∈H.

定理10.6 （判定定理二）

设G为群，H是G的非空子集. H是G的子群当且仅当a,b∈H

有ab^1∈H. 

定理10.7 （判定定理三）

设G为群，H是G的非空有穷子集，则H是G的子群当且仅当

a,b∈H有ab∈H.

定义10.7设G为群,令

C={a| a∈G∧x∈G(ax=xa)}，

则C是G的子群，称为G的中心.

定义10.9 设H是G的子群，a∈G.令

Ha={ha | h∈H}

称Ha是子群H在G中的右陪集. 称a为Ha的代表元素. 

定理10.8设H是群G的子群，则

(1) He = H

(2) a∈G 有a∈Ha

定理10.9设H是群G的子群，则a,b∈G有

  a∈Hb ab^1∈H Ha=Hb

定理10.10设H是群G的子群，在G上定义二元关系R：

a,b∈G, <a,b>∈R ab^1∈H

则 R是G上的等价关系，且[a]_R = Ha.

推论

设H是群G的子群, 则

(1) a,b∈G，Ha = Hb 或 Ha∩Hb = 

(2) ∪{Ha | a∈G} = G

定理10.11 设H是群G的子群，则a∈G，H ≈Ha

通过以上定理和推论可以知道：给定群G的一个子群H，H的所有右陪集的集合{Ha|a ∈G}恰好构成G的一个划分，而且可以进一步证明这个划分的所有划分块都与H等势。

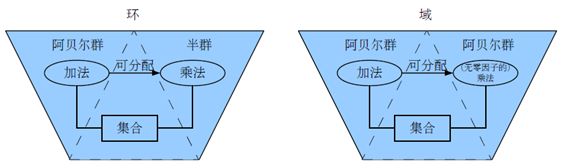
定义10.12 设<R,+,·>是代数系统，+和·是二元运算. 如果满足

以下条件:

(1) <R,+>构成交换群

(2) <R,·>构成半群

(3) · 运算关于+运算适合分配律

则称<R,+,·>是一个环.

通常称+运算为环中的加法，·运算为环中的乘法.

环中加法单位元记作 0，乘法单位元（如果存在）记作1.

对任何元素 x，称 x 的加法逆元为负元，记作x.

若 x 存在乘法逆元的话，则称之为逆元，记作x^1.

定理10.16 设<R,+,·>是环，则

(1) a∈R，a0 = 0a = 0

(2) a,b∈R，(a)b = a(b) = ab

(3) a,b,c∈R，a(bc) = abac， (bc)a = baca

(4) a₁,a₂,...,a_n,b₁,b₂,...,b_m∈R (n,m≥2)

定义10.13设<R,+,·>是环

(1) 若环中乘法 · 适合交换律，则称R是交换环

(2) 若环中乘法 · 存在单位元，则称R是含幺环

(3) 若a,b∈R，ab=0 a=0∨b=0，则称R是无零因子环

(4) 若R既是交换环、含幺环、无零因子环，则称R是整环

(5) 设R是整环，且R中至少含有两个元素. 若a∈R*，其中

R*=R{0}，都有a^－1∈R，则称R是域.

  

  

  

  

  

  

1.1：r，自于二么少二e高t/r

↳。七二心）上似"二e》rlt

  

G与〈。">：日akcG，G"二们一片

G三（0-'>{G口。。的一

•2个：假设G：

→：：a=b本

刁的b=am」

G=Gmt

消去：Gm山二e

无限阶必有mt=1

从而治""二，

•同三七二一/

  

  

互质是公约数只有1的两个整数，叫做互质整数。