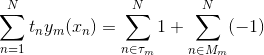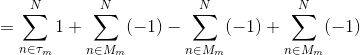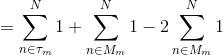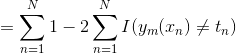集成算法学习(1)-Bagging、Boosting(AdaBoost)原理与公式推导
1、决策树与集成学习的关系
根据python3 决策树(ID3、C4.5、CART)原理详细说明与公式推导可知:
决策树容易解释,可以处理离散和连续值,对输入变量的单调转换不敏感(因为分割点是基于数据点的排序),执行自动变量选择,对异常值相对稳定,可以很好地扩展到大型数据集,并且可以修正输入的缺失值。
但是决策树与其他类型的模型相比,预测不是很准确。这部分是由于树构造算法的贪心本性。一个相关的问题是树是不稳定的:由于树生长过程的层次性,对输入数据的微小更改可能对树的结构产生很大的影响,导致树的顶部错误影响树的其他部分。
在频率学术语中,说树是高方差估计量。首先了解一下方差和偏差。
1.1 偏差-方差权衡
偏差-方差权衡是与机器学习监督算法尤其是预测建模相关的。这是一种通过分解预测误差来诊断算法性能的方法。
在机器学习中,算法只是一个可重复的过程,用于从给定的一组训练数据训练模型。对于给定训练数据,不同算法不同情境下训练效果不一样,一个关键的区别是它们产生了多少偏差和方差。
预测误差有三种类型:偏差、方差和不可减少误差(irreducible error)。
不可减少误差也被称为“噪声”,它不能由你选择的算法来减少。它通常来自固有的随机性、错误框架问题或不完整的特征集。
偏差(Bias)是模型的预测值与真实值之间的差异。比如用线性回归对曲线趋势的数据点进行建模,无论如何都不能很好的拟合曲线,这就是欠拟合(under-fitting).
方差(Variance)是指算法对特定训练数据集的敏感性或者可以描述为是预测值作为随机变量的离散程度。高方差算法会根据训练集产生截然不同的模型。能够拟合训练集的每个样本包括样本噪声,这就是过拟合。
算法不是一次性训练单个模型的方法,而是可重复的过程。假设已经为同一个问题收集了5个不同的训练集。使用一种算法来训练5个模型,每个模型对应一个训练集。偏差和方差是指算法训练的模型的准确性和一致性。
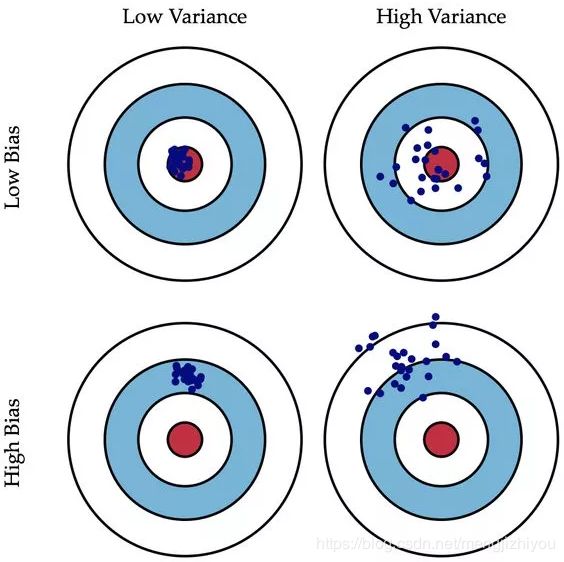
如下图所示(将左图中的每个点看做一个模型训练效果):
低方差高偏差算法往往不那么复杂,具有简单或严格的底层结构。他们训练的模型是一致的,但平均来说是不准确的。这些包括线性或参数算法,如回归和朴素贝叶斯。另一方面,低偏差高方差算法往往更复杂,具有灵活的底层结构。他们训练的模型平均来说是准确的,但不一致。这包括非线性或非参数算法,如决策树和最近邻。这种复杂性的权衡就是为什么会有偏差和方差的权衡——一个算法不能同时变得更复杂和更简单。*注意:对于某些问题,某些算法的这两个错误可能比其他算法少。例如,集成方法(即随机森林)在实践中往往比其他算法表现得更好。建议始终尝试多个合理的算法来解决每个问题。
要想偏差表现的好,就需要复杂化模型,增加模型的参数,但这样容易过拟合,过拟合对应上图(左)的 High Variance,点会很分散。低偏差对应的点都打在靶心附近,所以喵的很准,但不一定很稳;
要想方差表现的好,需要简化模型,减少模型的复杂度,但这样容易欠拟合,欠拟合对应上图(左) High Bias,点偏离中心。低方差对应就是点都打的很集中,但不一定是靶心附近,手很稳,但不一定瞄的准。
为了建立一个良好的预测模型,需要在偏差和方差之间找到一个平衡点,使总误差最小化,如上图(右)所示。
通过上面的介绍,大概知道偏差和方差的基本概念,下面介绍集成学习算法。
1.2 集成学习
集成学习是改进已有学习器的方法,并不是创建新的算法,而是将多个不同的算法和模型集成起来,创建一个集成学习器。集成学习的框架主要有bagging、boosting和stacking。
将多个决策树集成是集成学习的一种,除了使用多个一样的模型,集成学习也可将不同的模型集成。
集成学习中的基模型是弱模型,通常来说弱模型是偏差高(在训练集上准确度低)方差小(防止过拟合能力强)的模型。但是,并不是所有集成学习框架中的基模型都是弱模型。Bagging 和 Stacking 中的基模型为强模型(偏差低方差高),Boosting 中的基模型为弱模型。
集成学习(ensemble learning) 通过构建并结合多个学习器来完成学习任务,有时称多分类器系统(multi-classifier system)、基于委员会的学习(committee-based learning)等。
为什么集成学习会好于单个学习器呢?
-
训练样本可能无法选择出最好的单个学习器,由于没法选择出最好的学习器,所以干脆结合起来一起用;
-
假设能找到最好的学习器,但由于算法运算的限制无法找到最优解,只能找到次优解,采用集成学习可以弥补算法的不足;
-
可能算法无法得到最优解,而集成学习能够得到近似解。比如说最优解是一条对角线,而单个决策树得到的结果只能是平行于坐标轴的,但是集成学习可以去拟合这条对角线。
2、Bagging(Breiman, 1996)
减少估计的方差的一种方法是将多个估计平均起来,对得到的函数求平均值时,方差项的贡献趋于抵消,从而改进了预测。例如可以在数据的不同子集上训练M个不同的树,用替换随机选择(有放回重采样),然后计算集成:
这个过程被称为自助采样法或装袋 (bootstrap aggregation or bagging)。
因为 bagging 是有放回的随机采样,会有部分数据不会被抽取,未被抽取的概率在1/3,这部分数据叫 out of bag samples,因此可以用这部分数据对模型进行检验。
下面用回归函数说明 bagging比单个模型好。
假设要预测的回归函数是 ![]() ,则每个模型的输出都可以写成真值加上误差:
,则每个模型的输出都可以写成真值加上误差: ![]()
单个模型的平均误差平方和为: ![]()
委员会的期望误差误差平方和为: ![]()
上述结果表明:一个模型的平均误差可以通过简单地对模型的M个版本进行平均来减少M个因素,即bagging降低了偏差。不幸的是,这取决于一个关键的假设,即由各个模型引起的误差是不相关的。在实践中,错误通常是高度相关的,总体错误的减少通常很小。但是,可以表明,期望的委员会误差不会超过组成模型的预期误差,因此 ![]() 。为了实现更显著的改进,使用更复杂的技术建立委员会,称为boosting。
。为了实现更显著的改进,使用更复杂的技术建立委员会,称为boosting。
如果假设误差的均值为0且不相关,则有:
![]()
![]()
随机森林(Random forests,Breiman 2001)是 Bagging 的扩展变体,它在以决策树为基学习器构建 Bagging 集成的基础上,进一步在决策树的训练过程中引入了随机特征选择,因此可以概括 RF 包括四个部分:
-
随机选择样本(放回抽样);
-
随机选择特征;
-
构建决策树;
-
随机森林投票(平均)。
随机选择样本和 Bagging 相同,采用的是 Bootstrap 自助采样法;随机选择特征是指在每个结点在分裂过程中都是随机选择特征的(区别与每棵树随机选择一批特征)。
这种随机性导致随机森林的偏差会有稍微的增加(相比于单棵不随机树),但是由于随机森林的“平均”特性,会使得它的方差减小,而且方差的减小补偿了偏差的增大,因此总体而言是更好的模型。
随机采样由于引入了两种采样方法保证了随机性,所以每棵树都是最大可能的进行生长就算不剪枝也不会出现过拟合。
随机森林优点:
-
在数据集上表现良好,相对于其他算法有较大的优势
-
易于并行化,在大数据集上有很大的优势;
-
能够处理高维度数据,不用做特征选择。
总的来说就是bagging只是对样本有放回的随机抽取(采样),而随机森林是对样本和特征都进行有放回的随机抽取。
3、Boosting(Schapire and Freund 2012)
boosting 是bagging的一种增强版,通过改善模型表现不佳的地方提高学习器的效果。
boosting将多个基分类器(base classifiers)组合在一起,生成一个性能优于任何基分类器的委员会。
基分类器的性能只比随机分类器稍好一点,但Boosting(增强)也可以产生好的结果,因此有时基分类器被称为弱学习器(weak learners)。
最初设计用于解决分类问题(投票法),boosting也可以扩展到回归(Friedman, 2001)。
boosting 是可将弱学习器提升为强学习器的算法,其增强算法代表是 AdaBoost (adaptive boosting, Freund and Schapire,1996)。
补充:对于决策树来说,其在AdaBoost中的弱学习器是指决策树桩,即一个结点(根结点)和两个叶节点(只含有一个属性)。
3.1 AdaBoost(Freund and Schapire,1996)
AdaBoost是对基分类器按顺序进行训练,每个基分类器使用数据集的加权形式进行训练,其中每个数据点的加权系数取决于前一个分类器的性能。特别地,被一个基分类器错误分类的点在用于训练序列中的下一个分类器时被赋予更大的权重。一旦所有的分类器都经过了训练,它们的预测就会通过加权多数投票组合起来,如下图所示。
上图是Adaboost的框架示意图。每个基分类器 ![]() 都在训练集(蓝色箭头)的加权形式上进行训练,其中
都在训练集(蓝色箭头)的加权形式上进行训练,其中 ![]() 的权值取决于前一个基分类器
的权值取决于前一个基分类器 ![]() (绿色箭头)的性能。一旦所有基分类器都被训练好了,它们就会被组合成最终分类器
(绿色箭头)的性能。一旦所有基分类器都被训练好了,它们就会被组合成最终分类器 ![]() (红色箭头)。
(红色箭头)。
理解:首先构建一个bagging,随机从训练集中抽取一部分数据(有放回的抽样,bootsrap),接着训练模型得到模型 ![]() ,然后用这个模型对训练数据进行判别,会有一些样本判别错误;再一次构建bagging,随机抽取部分数据(可能含判断错误的数据),这时对判断错误的样本数据加大权重,然后训练模型得到
,然后用这个模型对训练数据进行判别,会有一些样本判别错误;再一次构建bagging,随机抽取部分数据(可能含判断错误的数据),这时对判断错误的样本数据加大权重,然后训练模型得到 ![]() ,一直持续下去,直到训练了M个模型。最后对所得到的的M个模型分配不同的权重相加,取符号即可。(注意:除了有放回抽样,也可以将所有训练样本用来训练模型)
,一直持续下去,直到训练了M个模型。最后对所得到的的M个模型分配不同的权重相加,取符号即可。(注意:除了有放回抽样,也可以将所有训练样本用来训练模型)
对于AdaBoost主要考虑二分类问题。假设训练数据包含输入向量 ![]() 及其相应目标变量
及其相应目标变量 ![]() ,则
,则 ![]() 。每个数据点都有一个相关的加权参数
。每个数据点都有一个相关的加权参数 ![]() ,该参数最初为1/N (N代表样本数)。在算法的每个阶段,AdaBoost使用一个数据集来训练一个新的分类器,其中的加权系数根据之前训练的分类器的性能进行调整,从而使错误分类的数据点获得更大的权重。最后,当训练了一定数量的基分类器时,赋予基分类器不同的权重并将它们组合起来组成一个委员会。
,该参数最初为1/N (N代表样本数)。在算法的每个阶段,AdaBoost使用一个数据集来训练一个新的分类器,其中的加权系数根据之前训练的分类器的性能进行调整,从而使错误分类的数据点获得更大的权重。最后,当训练了一定数量的基分类器时,赋予基分类器不同的权重并将它们组合起来组成一个委员会。
AdaBoost算法的精确形式如下所示:
1) 初始化数据权重 ![]() ,设置
,设置 ![]()
2) for ![]() :
:
a) 将分类器 ![]() 与训练数据进行拟合,并最小化加权误差函数:
与训练数据进行拟合,并最小化加权误差函数:
![]() 是指示函数(indicator function)。当
是指示函数(indicator function)。当 ![]() 时,
时,![]() ,否则为0。
,否则为0。
b) 评估数量:
![]()
![]() 表示数据集上每个基分类器的错误率的加权度量。
表示数据集上每个基分类器的错误率的加权度量。
c) 计算 ![]() :
:
![]()
![]() 的大小由树桩的误差分类率
的大小由树桩的误差分类率 ![]() 决定。
决定。![]() 越小表示决策树桩效果越差。
越小表示决策树桩效果越差。
d) 更新权重系数:
![]()
在随后的迭代中,对于误分类的数据点,加权系数 ![]() 增大,对于正确分类的数据点,加权系数
增大,对于正确分类的数据点,加权系数 ![]() 减小。因此,连续的分类器被迫更加强调那些被以前的分类器错误分类的点,而那些继续被连续的分类器错误分类的数据点将获得更大的权重。
减小。因此,连续的分类器被迫更加强调那些被以前的分类器错误分类的点,而那些继续被连续的分类器错误分类的数据点将获得更大的权重。
3) 更新最终的模型并用最终的模型进行预测:
计算的整体输出时 ,![]() 提供更大的权重给更准确的基分类器。
提供更大的权重给更准确的基分类器。
4) 当最终模型的误分率低于一定阈值或迭代次数达到一定值,停止迭代;否则,回到步骤 2)
下面对上面步骤中的公式进行说明和推导:
![]() ,
,![]()
![]() 是步长参数(learning rate),通常为 0.1 ,也叫伸缩因子(shrinkage),是为了防止 Adaboost 过拟合。对于同样的训练集学习效果,较小的 v 意味着我们需要更多的弱学习器的迭代次数。通常我们用步长和迭代最大次数一起来决定算法的拟合效果。
是步长参数(learning rate),通常为 0.1 ,也叫伸缩因子(shrinkage),是为了防止 Adaboost 过拟合。对于同样的训练集学习效果,较小的 v 意味着我们需要更多的弱学习器的迭代次数。通常我们用步长和迭代最大次数一起来决定算法的拟合效果。
算法的关键是不会回头去调整之前的参数,因此被称为前向阶段加性建模(forward stagewise additive modeling)。
目标是相对权重系数 ![]() 和基分类器参数
和基分类器参数 ![]() 最小化
最小化 ![]() 。假设
。假设 ![]() 是固定的,其对应系数为
是固定的,其对应系数为 ![]() ,所以最小化只需相对
,所以最小化只需相对 ![]() 和
和 ![]() 。将基分类器
。将基分类器 ![]() 的贡献分离出来,因此误差函数可以写为:
的贡献分离出来,因此误差函数可以写为:
![]()
将上式中的 ![]() 可以看做常数,因此只需优化
可以看做常数,因此只需优化 ![]() 和
和 ![]() 。用
。用 ![]() 表示基分类器
表示基分类器 ![]() 分类正确的点, 表示被分类错误的点,则误差函数可以写为:
分类正确的点, 表示被分类错误的点,则误差函数可以写为:
分类正确 : ![]()
分类错误: ![]()
上式相对 ![]() 求最小值,第一项为常数,因此相当于对第二项求最小值,与 AdaBoost算法步骤2) 的 a 步骤求
求最小值,第一项为常数,因此相当于对第二项求最小值,与 AdaBoost算法步骤2) 的 a 步骤求 ![]() 的最小值是一样的。因为求和前的整体乘性因子不影响最小值的位置。
的最小值是一样的。因为求和前的整体乘性因子不影响最小值的位置。
类似的,相对 ![]() 求最小值,可以得到
求最小值,可以得到 ![]() ,与 AdaBoost算法步骤2) 的 c 步骤的公式一致,下面是推导过程:
,与 AdaBoost算法步骤2) 的 c 步骤的公式一致,下面是推导过程:
↓↓↓↓↓
![]()
结合事实:![]() , 可得
, 可得 ![]() 在下一次迭代中更新可用下式:
在下一次迭代中更新可用下式:
![]()
上式中 独立于 ![]() ,对所有的点取一样权重或相同的因子,因此可以被丢弃,得到AdaBoost算法步骤2) 的 d 步骤的公式。
,对所有的点取一样权重或相同的因子,因此可以被丢弃,得到AdaBoost算法步骤2) 的 d 步骤的公式。
注:上述只适应于二分类问题(discrete AdaBoost),因为其假设 ![]() 返回的是二分类标签。如果
返回的是二分类标签。如果![]() 返回的是概率,则不可丢弃,这是修正后的算法,又叫 real AdaBoost。
返回的是概率,则不可丢弃,这是修正后的算法,又叫 real AdaBoost。
补充:![]() 证明:
证明:
最后所有基分类器都被训练完,用  对新的数据点进行预测。因为前面的
对新的数据点进行预测。因为前面的 ![]() 对取符号没有影响,因此可以省略,得到 AdaBoost算法步骤 3) 的公式。
对取符号没有影响,因此可以省略,得到 AdaBoost算法步骤 3) 的公式。
上述指数损失函数给错分类点过多的权重,如下图所示(红线,左侧)。这使得该方法对异常值(错分的点)非常敏感。此外,![]() 不是
不是 ![]() 的概率分布的对数,因此无法从 f(x) 中重新获得概率估计。
的概率分布的对数,因此无法从 f(x) 中重新获得概率估计。
一种替代方法是使用 logloss,这只会线性地惩罚错误 (如下图所示) 并能够从最终的学习函数中提取概率。
AdaBoost:
- 优点:分类精度高;可以用各种回归分类模型来构建弱学习器,非常灵活;不容易发生过拟合;只能用于二分类,但可扩展到多分类和回归。
- 缺点:对异常点敏感,异常点会获得较高权重。
补充:随机森林与AdaBoost的比较:
- 决策树属性和深度的选取:随机森林的每个模型采用随机样本选取和随机特征选取,对树的深度不做要求;AdaBoost构建的每棵树(决策树桩)只有一个属性和两个叶节点。
- 单个模型的准确度:随机森林的单个模型可以选取所有样本和所有特征构建决策树,模型的准确率高(偏差低),因此随机森林(Bagging)的模型是强学习器;AdaBoost的单个模型是决策树桩,只有一个属性,所以准确率低(偏差高),因此决策树桩(Boosting)是弱学习器。
- 模型的有序性:随机森林从训练数据中有放回的随机抽取样本和特征,然后构建决策树模型,各个模型之间是无序的,即模型之间是独立的,无需注意哪个模型是先建立的还是后建立的。AdaBoost是有序的,第一个树桩的误差会影响第二个树桩,第二个树桩的误差会影响第三个误差等等。
- 随机森林的每棵树在分类中都有相同权重;AdaBoost的每个树桩有不同的权重,一些树桩权重大,在最终函数中占比大。
3.2 Gradient boosting(Friedman 2001; Mason et al. 2000)
Gradient Boost与传统的Boost的区别是,每一次的计算是为了减少上一次的残差(residual)梯度提升方法在迭代的每一步构建一个能够沿着梯度最陡的方向降低损失(steepest-descent)的学习器来弥补已有模型的不足。
经典的AdaBoost算法只能处理采用指数损失函数的二分类学习任务,而梯度提升方法通过设置不同的可微损失函数可以处理各类学习任务(多分类、回归、Ranking等),应用范围大大扩展。
另一方面,AdaBoost算法对异常点(outlier)比较敏感,而梯度提升算法通过引入bagging思想、加入正则项等方法能够有效地抵御训练数据中的噪音,具有更好的健壮性。
GBDT 的核心在于累加所有树的结果作为最终结果,GBDT 的每一棵树都是以之前树得到的残差来更新目标值,这样每一棵树的值加起来即为 GBDT 的预测值。
具体见:Boosting(GBDT回归)(举例说明,通俗易懂)
Boosting(GBDT分类)(举例说明,通俗易懂)
GBDT:
- 优点:可以自动进行特征组合,拟合非线性数据;适用于线性非线性回归,二分类和多分类。
- 缺点:对异常点敏感。
Gradient boosting与 Adaboost 的对比
相同:
-
都是 Boosting 家族成员,使用弱分类器;
-
都使用前向分布算法;
不同:
-
迭代思路不同:Adaboost 是通过提升错分数据点的权重来弥补模型的不足(利用错分样本),而 GBDT 是通过算梯度来弥补模型的不足(利用残差);
-
损失函数不同:AdaBoost 采用的是指数损失,GBDT 使用的是绝对损失或者 Huber 损失函数;
4、Stacking(Wolpert 1992)
Stacking 是先用全部数据训练好基模型,然后每个基模型都对每个训练样本进行的预测,其预测值将作为训练样本的特征值,最终会得到新的训练样本,然后基于新的训练样本进行训练得到模型,然后得到最终预测结果。
5、Python3
参考:Boosting(AdaBoost) 算法实现


![E_{AV}=\frac{1}{M}\sum_{m=1}^M E_x\left [ \epsilon_m (x)^2 \right ]](http://img.e-com-net.com/image/info8/964f7c35ffab49a6a5cad0b7432478f4.gif)
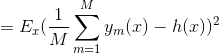
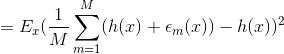
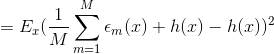

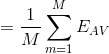


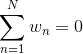
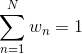

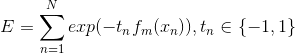



![+[exp(\frac{1}{2}\alpha_m)-exp(-\frac{1}{2}\alpha_m)]\sum_{n=1}^N w_n^{(m)} I(y_m(x_n)\neq t_n)](http://img.e-com-net.com/image/info8/f23b2d5d75bb474896a051a76fff5ee9.gif)
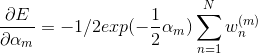
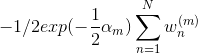
![=-[1/2exp(\frac{1}{2}\alpha_m)+1/2exp(-\frac{1}{2}\alpha_m)]\sum_{n=1}^N w_n^{(m)} I(y_m(x_n)\neq t_n)](http://img.e-com-net.com/image/info8/c12093af2af845668941873c30ca8f0d.gif)
![exp(-\frac{1}{2}\alpha_m)/[exp(\frac{1}{2}\alpha_m)+exp(-\frac{1}{2}\alpha_m)]=\frac{ \sum_{n=1}^N w_n^{(m)}I(y_m(x_n)\neq t_n)}{\sum_{n=1}^N w_n^{(m)}}](http://img.e-com-net.com/image/info8/a78107141ed348f5ba3de54c93c6a897.gif)