正确区分大小端模式

正确区分大小端模式

嵌入式开发经常会遇到大小端的问题，往往学习后，过一段时间就又忘记了，这里总结一下，希望给大家留下深刻的记忆。

字节顺序是指占内存多于一个字节类型的数据在内存中的存放顺序，通常有小端和大端两种字节顺序，这两种你只需要深刻地记住其中的一种就可以，另一种恰好和它相反，不需要刻意记忆了，那么我们就记住“大端模式”吧。

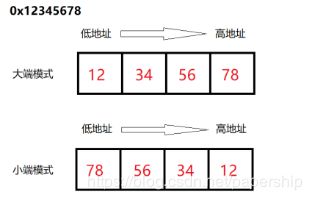
大端模式（Big-Endian）：是指数据的高字节保存在内存的低地址中，而数据的低字节保存在内存的高地址中。

说明：通常数据在内存中的存储是按照内存地址由低地址到高地址的顺序存储的，大端模式有点儿类似于把数据看做是一个字符串，然后按照字符串从左到右的顺序来存储，地址由小向大增加，而数据从高位往低位放，数据的存储方向和我们的阅读习惯（方向）一致。

小端模式（Little-Endian）：是指数据的高字节保存在内存的高地址中，而数据的低字节保存在内存的低地址中。数据的存储方向和我们的阅读习惯（方向）不一致。

例子如下：

初学者往往被一些信息误导，而有这样的疑惑，例如：操作系统是大端还是小端存储？编译器是大端还是小端编译？CPU是大端还是小端？

其实，大小端主要有用于存储的顺序，与存储器（硬件）关系比较大，编译器和操作系统仅仅是配合CPU编译好相应的代码，而不是决定大小端的因素，因此大小端模式还是与CPU有关，而与编译器和操作系统没有直接关系。

如何判断大小端模式

大小端的判断方法很多，比较直观的是利用强制类型转换来判断，我们需要定义一个字节长度的指针，例如char型指针，指向int型的低位地址，同时需要将int型数据强制转换为char型的数据。

void FunJudge(void)

{

    int i = 0x12345678;

    char *p,ch;

    i = 0x12345678;

    ch = (char)i;          /* 强制类型转换成char型，将取低位地址存储的数据 */

    p = &ch;

    if(*p == 0x12)        /* 低位地址存储的是数据的高位字节，则为大端 */

    {

        printf("大端模式\n");

    }

    else

    {

        printf("小端模式\n");

    }

}

大小端的相互转换

通过前面的学习，我们知道大小端模式与CPU有关，在进行系统移植的时候，由于使用的硬件平台不同，因此就需要进行大小端模式的转化。

下面举例说明如何进行大小端模式的转换。

例：原数据为0x12345678是按照大端模式存放的，现在需要转化为小端模式。

一、利用宏定义形式实现

#include "stdio.h"

#define CONVERT(x) (((x&0xff)<<24)|((x&0xff00)<<8)|((x&0xff0000)>>8)|((x&0xff000000)>>24))       

说明：

1、利用C语言的按位与、按位左移和按位右移来实现

2、x表示被转换的数据，例如这里的0x12345678是被转化数据。

3、转换前四个字节的排列顺序要弄清楚

二、利用函数形式实现

void ConvertToLittle(int x)
{
    char a,b,c,d;

    /* 将数据的每一个字节取出分别保存到4个变量中 */

    a = (char)(x&0xff);

    b = (char)((x&0xff00)>>8);

    c = (char)((x&0xff0000)>>16);

    d = (char)((x&0xff000000)>>24);

    /* 将4个字节的数据分别移动不同的位数，组合成新的数据 */
    x = (a<<24)|(b<<16)|(c<<8)|d;
    printf(“transfered x is 0x%x\n”,x);
}

/* 通过main函数来验证2种方式的转换 */

int main()
{
    int num;
    printf(“please input the number:\n”);
    scanf(“%d”,&num);
    printf(“The number you input is 0x%x\n”,num);
    ConvertToLittle(num);
    printf(“macro transfered: 0x%x\n”,CONVERT(num));
}

总结：通过以上2种方法实现了大端模式到小端模式的转换，小端模式转换为大端模式也是一样的，这里不做详细说明。