ML-项目-181227-电信公司客户流失项目

建模大致思路

1. 数据读取
2. 数据清洗
3. 两变量假设检验
4. 划分训练集和测试集
5. 使用训练集做模型进行预测
6. 模型检验（混淆矩阵、ROC)
7. 模型调优(向前法去除不显著变量、多重共线性)

各变量解释

#subscriberID=“个人客户的ID”
#churn=“是否流失：1=流失”;
#Age=“年龄”
#incomeCode=“用户居住区域平均收入的代码”
#duration=“在网时长”
#peakMinAv=“统计期间内最高单月通话时长”
#peakMinDiff=“统计期间结束月份与开始月份相比通话时长增加数量”
#posTrend=“该用户通话时长是否呈现出上升态势：是=1”
#negTrend=“该用户通话时长是否呈现出下降态势：是=1”
#nrProm=“电话公司营销的数量”
#prom=“最近一个月是否被营销过：是=1”
#curPlan=“统计时间开始时套餐类型：1=最高通过200分钟；2=300分钟；3=350分钟；4=500分钟”
#avPlan=“统计期间内平均套餐类型”
#planChange=“统计期间是否更换过套餐：1=是”
#posPlanChange=“统计期间是否提高套餐：1=是”
#negPlanChange=“统计期间是否降低套餐：1=是”
#call_10086=“拨打10086的次数”

1.数据读取

首先读入数据

#%%
import os
import pandas as pd
#%%
os.chdir(r'D:\data_py\chapter5\ML_project_181227_chapter5')
telecom_churn=pd.read_csv('telecom_churn.csv')

数据有3463个观测，20个变量。

2.数据清洗

判断数据有多少的NA

telecom_na=pd.isna(telecom_churn)

for name in telecom_na.columns:
   print(telecom_na[name].value_counts())

输出结果如图，发现该数据集并无NA

3.两变量假设检验

检验posTrend和churn是否相关，因为两变量均为离散性变量，先做列联表

cross_table=pd.crosstab(telecom_churn.posTrend,telecom_churn.churn,margins=True)
cross_table

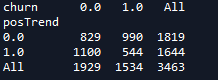
可见posTrend为1的人流失的比例相对为0的人更少
不妨将列联表化为百分比形式

def percConvert(ser):
   return ser/float(ser[2])

cross_table_pct=cross_table.apply(percConvert,axis=1)
cross_table_pct

可见posTrend为0的人违约概率54.4%，为1的人违约概率为33.1%
对两变量进行卡方检验判断相关性

from scipy import stats
print('''chisq=%6.4f
      p-value=%6.4f
      dof=%i
      expected_freq=%s''' %stats.chi2_contingency(cross_table.iloc[:2,:2]))   

可见非常显著

4.划分训练集与测试集

train=telecom_churn.sample(frac=0.7,random_state=1234).copy()
test=telecom_churn[~telecom_churn.index.isin(train.index)].copy()
print('训练集样本量: %i \n测试集样本量: %i'%(len(train),len(test)))

划分后得到训练集2424样本，测试集1039样本

5.使用训练集模型进行预测

5.1单变量预测posTrend，churn

import statsmodels.formula.api as smf
import statsmodels.api as sm
lg=smf.glm('churn~posTrend',data=telecom_churn,family=sm.families.Binomial(sm.families.links.logit)).fit()

lg.summary()

可见
[图片插入]
5.2多变量逻辑回归
对于逻辑回归来说，因变量必须是分类变量，自变量可以是连续变量也可以是分类变量。

#incomeCode#peakMinAv#nrProm#curPlan#avgplan#planChange#negPlanChange 均不相关
formula='''
churn~gender+AGE+edu_class+incomeCode+duration+feton+peakMinAv+peakMinDiff+posTrend+negTrend+nrProm+
curPlan+avgplan+planChange+negPlanChange+call_10086'''

lg_m=smf.glm(formula=formula,data=train,family=sm.families.Binomial(sm.families.links.logit)).fit()

lg_m.summary()

以下变量与churn无相关性，将从模型中剔除
#incomeCode
#peakMinAv
#nrProm
#curPlan
#avgplan
#planChange
#negPlanChange

6.模型检验

7.模型调优

7.1通过向前法进行模型调优

candidates=['churn','gender','AGE','edu_class','incomeCode','duration','feton','peakMinAv','peakMinDiff','posTrend','negTrend','nrProm','curPlan','avgplan','planChange','negPlanChange','call_10086']
data_for_select=train[candidates]
lg_m1=forward_select(data=data_for_select,response='churn')

向前法操作后，变量由16个变为11个
重新做逻辑回归

formula='''
churn ~ duration + feton + gender + call_10086 + peakMinDiff + edu_class + AGE + posTrend + negTrend + peakMinAv + nrProm'''

lg_m1=smf.glm(formula=formula,data=train,family=sm.families.Binomial(sm.families.links.logit)).fit()

lg_m1.summary()

?回想起似乎向前法只能做一次，删掉不相关的变量后依然会有新的p值大于阈值的变量出现。?

7.2判断是否存在多重共线性

定义vif判别函数

def vif(df,col_i):
    from statsmodels.formula.api import ols
    
    cols=list(df.columns)
    cols.remove(col_i)
    cols_noti=cols
    formula =  col_i + '~' + '+'.join(cols_noti)
    r2=ols(formula,df).fit().rsquared
    return 1./(1. -r2)

exog=train[candidates].drop(['churn'],axis=1)

for i in exog.columns:
    print(i,'\t',vif(df=exog,col_i=i))

可见posTrend和negTrend存在共线性，curPlan和avgplan存在共线性
删除negTrend和curPlan

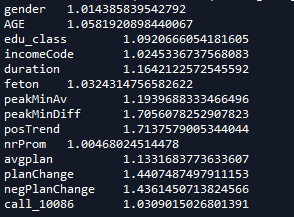
可见多重共线性消失
同时删除3个不显著变量posTrend + peakMinAv + nrProm
得到模型

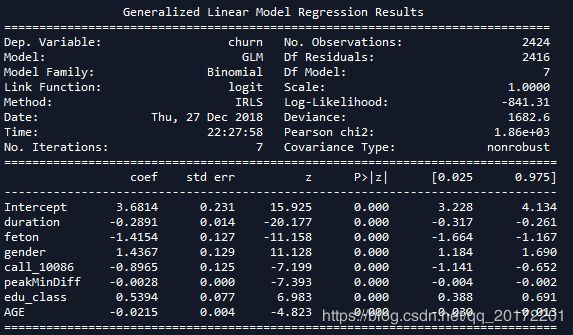
7.3输出模型流失概率

train['proba']=lg_m1.predict(train)
test['proba']=lg_m1.predict(test)

test['proba'].head()    

test['prediction']=(test['proba']>0.5).astype('int')

输出结果如下

8.模型评估

首先计算模型预测准确率

import numpy as np
acc=sum(test['prediction']==test['churn'])/np.float(len(test))
print('The accurancy is %.2f' %acc)

预测准确率为0.82
接下来绘制混淆矩阵

pd.crosstab(test.churn,test.prediction,margins=True)

计算可得召回率达到368/456=0.807
根据f1_score计算可得最佳的阈值应该设为0.3

for i in np.arange(0,1,0.1):
    prediction=(test['proba']>i).astype('int')
    confusion_matrix=pd.crosstab(test.churn,prediction,margins=True)
    precision=confusion_matrix.ix[1,1]/confusion_matrix.ix['All',1]
    recall=confusion_matrix.ix[1,1]/confusion_matrix.ix[1,'All']
    f1_score=2*(precision*recall)/(precision+recall)
    print('threshold: %s, precision: %.2f,recall: %.2f,f1_score: %.2f'%(i,precision,recall,f1_score))

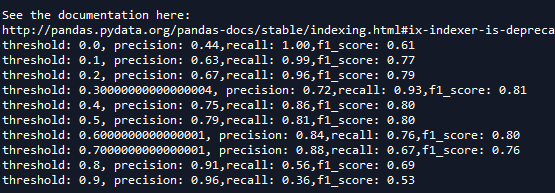
重新计算模型，准确率降为0.81，召回率升为92.5%

绘制ROC曲线

import sklearn.metrics as metrics
import matplotlib.pyplot as plt

fpr_test, tpr_test, th_test=metrics.roc_curve(test.churn,test.proba)
fpr_train,tpr_train,th_train=metrics.roc_curve(train.churn,train.proba)

plt.figure(figsize=[3,3])
plt.plot(fpr_test,tpr_test,'b--')#虚线
plt.plot(fpr_train,tpr_train,'r-')#实线
plt.title('ROC curve')
plt.show()

测试集（虚线）与训练集（实线）拟合的非常好，存在过拟合的可能性较小

print('AUC=%.4f'%metrics.auc(fpr_test,tpr_test))

计算AUC值，再次发现AUC值与阈值无关

END