排列组合-c语言-暴力&深搜

c语言实现排列组合的一种方法

1.全排列

2.全组合

一.全排列

先介绍一种第一种算法

for循环嵌套，然后判断，当循环数均不相等时输出
下面是一个例子来实现A(3,3)：

#include
int main()
{
	int i,j,k;
	for(i=1;i<=3;i++)
	{
		for(j=1;j<=3;j++)
		{
			for(k=1;k<=3;k++)
			{
				if(i!=j&&i!=k&&j!=k)        //判断循环数，不相等时输出
				{
					printf("%d %d %d\n",i,j,k);
				}
			}
		}
	}
	
	
	return 0;
}

执行结果如下：

如果要实现A(9,9)，代码会变成酱紫

#include
int main()
{
	int a1,a2,a3,a4,a5,a6,a7,a8,a9;
	for(a1=1;a1<10;a1++)
	{
		for(a2=1;a2<10;a2++)
		{
			for(a3=1;a3<10;a3++)
			{
				for(a4=1;a4<10;a4++)
				{
					for(a5=1;a5<10;a5++)
					{
						for(a6=1;a6<10;a6++)
						{
							for(a7=1;a7<10;a7++)
							{
								for(a8=1;a8<10;a8++)
								{
									for(a9=1;a9<10;a9++)
									{
										if(a1!=a2&&a1!=a3&&a1!=a4&&a1!=a5&&a1!=a6&&a1!=a7&&a1!=a8&&a1!=a9&&
										a2!=a3&&a2!=a4&&a2!=a5&&a2!=a6&&a2!=a7&&a2!=a8&&a2!=a9&&a3!=a4&&a3!=a5
										&&a3!=a6&&a3!=a7&&a3!=a8&&a3!=a9&&a4!=a5&&a4!=a6&&a4!=a7&&a4!=a8&&a4!=a9
										&&a5!=a6&&a5!=a7&&a5!=a8&&a5!=a9&&a6!=a7&&a6!=a8&&a6!=a9&&a7!=a8&&a7!=a9&&a8!=a9)
										printf("%d %d %d %d %d %d %d %d %d\n",a1,a2,a3,a4,a5,a6,a7,a8,a9);
									}
								}								
							}
						}
					}
				}
			}
		}
	}
	return 0;
}

我们会发现如果我们想从键盘读入一个n或者当n特别大时，代码会变得非常臃肿，所以我们今天介绍另一种方法：

首先我们需要了解一个简单的算法->深度搜索(dfs)
在这里我就不多赘述了。

下面我们用dfs来实现这个功能

#include
int n,a[100],book[100];
void dfs(int step);
int main()
{
	
	scanf("%d",&n);
	dfs(1);
	
	return 0;
}
void dfs(int step)
{
	int i;
	if(step==n+1)
	{	
		int sum=0;
		for(i=1;i<=n;i++)
		{
			printf("%d ",a[i]);
		}
		printf("\n");
		return;
	}

	for(i=1;i<=n;i++)
	{
		if(book[i]==0)
		{
			a[step]=i;
			book[i]=1;
			dfs(step+1);
			book[i]=0;
		}
	}	
	return;
}

当输入4时执行结果如下：

二.全组合

前面我们使用深搜(dfs)实现了全排列，要实现全组合我们只需要稍作改动：
代码如下：

#include
int n,k,a[11],book[11];
void dfs(int step);
int main()
{
	scanf("%d %d",&n,&k);         //这里加入了k
	dfs(1);
	return 0;
}
void dfs(int step)
{
	
	int i;
	if(step==k+1)
	{	
		
		for(i=1;i<=k-1;i++)         //  这段代码的作用是实现去重，具体解释在后面
		{							
			if(a[i]>a[i+1])			
			return;					
		}                           
		for(i=1;i<=k;i++)
		{
			printf("%d ",a[i]);
		}
		printf("\n");
		return;
	}

	for(i=1;i<=n;i++)
	{
		if(book[i]==0)
		{
			a[step]=i;
			book[i]=1;
			dfs(step+1);
			book[i]=0;
		}
	}
}

当输入5，3时运行结果

注释

for(i=1;i<=k-1;i++)
{
if(a[i]>a[i+1])
return;
}
当删去上面这段代码并输入4，3时我们会得到这样的结果

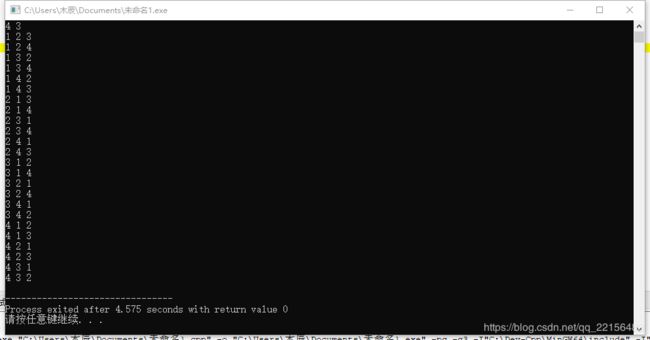
显然这是从n个数中取出k个并全排列的结果
观察发现1 2 3在里面出现了六次，分别是：
1 2 3
1 3 2
2 1 3
2 3 1
3 2 1
3 1 2
要实现去重我们只需让：第一个数<第二个数<第三个数
用代码实现便是
for(i=1;i<=k-1;i++)
{
if(a[i]>a[i+1])
return;
}