【一】 数据结构之Vector
【一】 数据结构之Vector
我们这里的数据结构是C++版本的,需要对C++有一点了解
内容大部分来源于网络视频课程,这里推荐观看学堂在线,自主课堂的邓俊辉老师的数据结构课程。
向量是一种抽象数据类型ADT,与数组不同,它提供了很多接口,能够实现更多的功能。如何理解ADT抽象数据类型,看下面这幅图片(图片均来源于学堂在线,引用请标注出处)
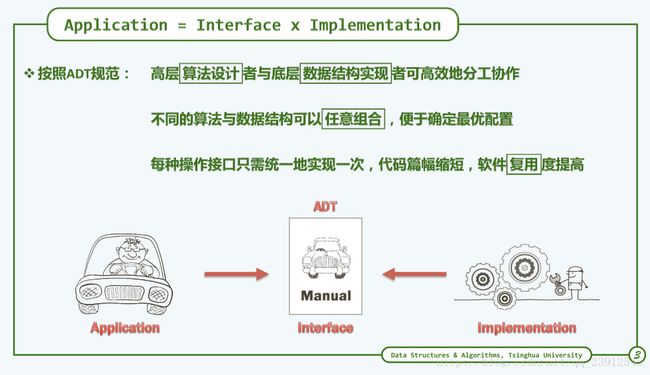
OK那么Vector给我们提供了哪些接口呢?
#ifndef VECTOR_H
#define VECTOR_H
#include "Fib.h"
typedef int Rank;//秩
#define DEFAULT_CAPACITY 3 //默认的初始容量
template class Vector{ //向量模板类
protected:
Rank _size; int _capacity; T* _elem;//规模、容量、数据区
void copyFrom(T const *A, Rank lo, Rank hi);//复制数组区间A[lo,hi)
void expand();//空间不足时扩容
void shrink();//装填因子过小时压缩
Rank bubble(Rank lo, Rank hi);//扫描交换
void bubbleSort(Rank lo, Rank hi);//起泡排序算法
Rank max(Rank lo, Rank hi);//选取最大元素
void selectionSort(Rank lo, Rank hi);//选择排序算法
void merge(Rank lo, Rank mi, Rank hi);//归并算法
void mergeSort(Rank lo, Rank hi);//归并排序算法
Rank partition(Rank lo, Rank hi);//轴点构造算法
void quickSort(Rank lo, Rank hi);//快速排序算法
void heapSort(Rank lo, Rank hi);//堆排序
public:
//构造函数
Vector(int c = DEFAULT_CAPACITY,int s = 0 ,T v = 0){ //容量为c,规模为s,所有元素初始化v
_elem = new T[_capacity = c];
for (_size = 0; _size < s; _elem[_size++] = v);//s<=c
}
Vector(T const *A, Rank n){//数组整体复制
copyFrom(A, 0, n);
}
Vector(T const *A, Rank lo, Rank hi){//数组区间
copyFrom(A, lo, hi);
}
Vector(Vector const& V, Rank lo, Rank hi){//向量区间
copyFrom(V._elem, lo, hi);
}
Vector(Vector const& V){//向量整体复制
copyFrom(V._elem, 0, v._size);
}
//析构函数
~Vector(){
delete[] _elem;//释放空间
}
//只读访问接口
Rank size() const{ return _size; }//规模
bool empty() const{ return !_size; }//判空
int disordered() const;//判断向量是否已排序
Rank find(T const& e) const { return find(e, 0, _size); }//无序向量整体查找
Rank find(T const &e, Rank lo, Rank hi) const;//无序向量区间查找
Rank search(T const& e) const{//有序向量整体查找
return(0 >= _size) ? -1 : search(e, 0, _size);
}
Rank search(T const& e, Rank lo, Rank hi) const;//有序向量区间查找
//可写访问接口
T& operator[] (Rank r) const;//重载下标操作符
Vector & operator= (Vector const&); //重载赋值操作符以便于克隆向量
T remove(Rank r);//删除秩为r的元素
int remove(Rank lo, Rank hi);//删除秩在区间[lo,hi)之内的元素
Rank insert(Rank r, T const& e);//插入元素
Rank insert(T const& e){ return insert(_size, e); }//默认作为末元素插入
void sort(Rank lo, Rank hi);//对[lo,hi)排序
void sort(){ sort(0, _size); }//整体排序
void unsort(Rank lo, Rank hi);//对[lo,hi)置乱
void unsort(){ unsort(0, _size); }//整体置乱
int deduplicate();//无序去重
int uniquify();//有序去重
//遍历
void traverse(void(*visit)(T&));//遍历(使用函数指针,只读或者局部性修改)
template void traverse(VST&);//遍历(使用函数对象,可全局性修改)
};
//函数定义
template
void Vector::copyFrom(T const *A, Rank lo, Rank hi){
_elem = new T[_capacity = 2 * (hi - lo)];//分配空间
_size = 0;//规模清零
while (lo < hi)//[lo,hi)内的元素逐一
_elem[_size++] = A[lo++];//复制到_elem[0,hi-lo)
}
template
void Vector::expand(){
if (_size < _capacity) return;//尚未满员,不必扩容
if (_capacity < DEFAULT_CAPACITY)_capacity = DEFAULT_CAPACITY;//不低于最小容量
T* oldElem = _elem;
_elem = new T[_capacity <<= 1];//容量倍增
for (int i = 0; i < _size; i++)
_elem[i] = oldElem[i];//T为基本类型,或者已经重载复制操作符"="
delete[] oldElem;//释放原空间
}
template
Rank Vector::insert(Rank r, T const& e){//插入操作
expand();//若有必要扩容
for (int i = _size; i > r; i--)//自后向前
_elem[i] = _elem[i - 1];
_elem[r] = e; _size++; return r;//置入新元素,更新容量,返回秩
}
template
void Vector::traverse(void(*visit)(T &)){//利用函数指针机制,只读或者局部性修改
for (int i = 0; i < _size; i++)
visit(_elem[i]);//遍历向量
}
template template
void Vector::traverse(VST& visit){//借助函数对象机制
for (int i = 0; i < _size; i++)
visit(_elem[i]);//遍历向量
}
template
int Vector::disordered() const{
int n = 0;
for (int i = 1; i < _size; i++)
n += (_elem[i - 1]>_elem[i]);//逆序则计数
return n;//向量有序当且仅当n=0
}
template
T& Vector::operator[](Rank r) const{//重载下标操作符
return _elem[r]; //0 <= r < _size
}
template
int Vector::remove(Rank lo, Rank hi){//区间删除[lo,hi)
if (lo == hi) return 0;//单独处理退化情况
while (hi < _size) _elem[lo++] = _elem[hi++];//[hi, _size)顺次前移
_size = lo; shrink();//更新规模,若有必要则缩容
return hi - lo;//返回被删除元素的数目
}
template
T Vector::remove(Rank r){//单元素删除,可作为区间删除的特例
T e = _elem[r];//备份删除的元素
remove(r, r + 1);//调用区间删除算法
return e;//返回被删除的元素
}
template
void Vector::shrink(){
if (_capacity < DEFAULT_CAPACITY << 1)return;//不至于收缩到DEFAULT_CAPACITY以下
if (_size << 2>_capacity)return;//已25%为界
T* oldElem = _elem; _elem = new T[_capacity >>= 1];//容量减半
for (int i = 0; i < _size; i++) _elem[i] = oldElem[i];//复制原内容
delete[] oldElem;//释放原空间
}
template
Rank Vector::find(T const & e, Rank lo, Rank hi) const{//无序向量的顺序查找:返回最后一个元素e的位置;失败时,返回lo-1
while ((lo < hi--) && (e != _elem[hi]));//从后顺序查找
return hi;//若hi
}
template
int Vector::deduplicate(){//无序向量去重操作
int oldSize = _size;//记录原规模
Rank i = 1;
while (i < _size)
(find(_elem[i], 0, i) < 0) ?
i++ ://若无雷同则继续向后考察
remove(i);//否则删除重复元素
return oldSize - _size;//返回规模变化量 即被删除元素的个数
}
template
int Vector::uniquify(){//有序向量重复去重算法(高效版)
Rank i = 0, j = 0;//各对互异元素的秩
while (++j<_size)
if (_elem[i] != _elem[j])
_elem[++i] = _elem[j];//发现不同时向前移动至前者的紧邻右侧
_size = ++i; shrink();//直接劫除尾部多余元素
return j - i;//向量规模变化量,即被删除元素的个数
}
template
void Vector::sort(Rank lo, Rank hi){//向量区间[lo,hi)排序
switch (rand()%5){//随机选取排序算法。可根据具体问题的特点灵活选取或者扩充
case 1:bubbleSort(lo, hi); break;//起泡排序
case 2:selectionSort(lo, hi); break;//选择排序
case 3:mergeSort(lo, hi); break;//归并排序
case 4:heapSort(lo, hi); break;//堆排序
default:quickSort(lo, hi);//快速排序
}
}
template
Rank Vector::search(T const& e, Rank lo, Rank hi) const{//在有序向量的区间[lo,hi)内,确定不大于e的最后一个节点的秩
return(rand() % 2) ? binSearch(_elem, e, lo, hi) : fibSearch(_elem, e, lo, hi);//各按照50%随机使用二分查找和fibonacci查找
}
template
void Vector::bubbleSort(Rank lo, Rank hi){//向量的起泡排序
while (lo < (hi = bubble(lo, hi)));//逐趟做扫描交换直至全序
}
template
Rank Vector::bubble(Rank lo, Rank hi){//一趟扫描交换
Rank last = lo;//最右侧的逆序对初始化为[lo-1,lo]
while (++lo//自左向右,逐一检查各对相邻元素
if (_elem[lo - 1]>_elem[lo]){
last = lo;//更新最右侧逆序对位置记录,并
swap(_elem[lo - 1], _elem[lo]);//通过交换使局部有序
}
return last;//返回最右侧的逆序对位置
}
/*
template
void swap(T const& A, T const& B){//交换两个T类型元素
T C = B;
B = A; A = C;
}
*/
template
void Vector::mergeSort(Rank lo, Rank hi){
if (hi - lo < 2) return;//单元素区间自然有序,否则。。。
int mi = (lo + hi) / 2;//以中点为界
mergeSort(lo, mi);//分别排序
mergeSort(mi, hi);
merge(lo, mi, hi);//归并
}
template//有序向量的归并
void Vector::merge(Rank lo, Rank mi, Rank hi){//各自有序子向量[lo,mi) 和[mi,hi)
T* A = _elem + lo;//合并后的向量A[0,hi - lo) = _elem[lo,hi)
int lb = mi - lo; T*B = new T[lb];//前子向量B[0,1b)= _elem[lo,mi)
for (Rank i = 0; i < lb; i++)B[i] = A[i];//复制前子向量
int lc = hi - mi; T* C = _elem + mi;//后子向量C[0,1c) = _elem[mi,hi)
for (Rank i = 0, j = 0, k = 0; (j < lb) || (k < lc);){//B[j] 和 C[k]中的小者续至A末尾
if ((j < lb) && (!(k < lc) || (B[j] <= C[k]))) A[i++] = B[j++];
if ((k < lc) && (!(j < lb) || (C[k] <= B[j]))) A[i++] = C[k++];
}
delete[] B;//释放临时空间B
}//归并后得到完整的有序向量[lo,hi)
//模板方法
//Fibonacci查找算法(版本A)
template
static Rank fibSearch(T* A, T const & e, Rank lo, Rank hi){
Fib fib(hi - lo);//用O(log_phi(n = hi - lo)时间创建Fib数列
while (lo < hi){//每次迭代可能要做两次比较判断,有三个分支
while (hi - lo < fib.get()) fib.prev();//通过向前顺序查找 至多迭代几次?
Rank mi = lo + fib.get() - 1;//确定形如Fib(k) -1 的轴点
if (e < A[mi]) hi = mi;//深入前半段[lo,mi)继续查找
else if (A[mi] < e) lo = mi + 1;//深入后半段(mi,hi)继续查找
else return mi;//在mi处命中
}//成功查找可以提前终止
return -1;//查找失败
}//有多个命中的元素时,不能保证返回秩最大者,失败时简单返回-1,不能确定失败的位置
//////////////////////////////////////////////////////////////////////////////
/*
//二分查找算法(版本A):在有序向量的区间[lo, hi)内查找元素e
template
static Rank binSearch(T* A, T const & e, Rank lo, Rank hi){
while (lo < hi){//每次迭代可能要做两次比较判断,有三个分支
Rank mi = (lo + hi) >> 1;//以中点为轴点
if (e < A[mi])hi = mi;//深入前半段[lo,mi)继续查找
else if (A[mi] < e) lo = mi + 1;//深入后半段(mi,hi)继续查找
else return mi;//在mi处命中
}//成功查找提前终止
return -1;//查找失败
}//有多个命中的元素时,不能保证返回秩最大者,失败时简单返回-1,不能确定失败的位置
//二分查找算法(版本B)
template
static Rank binSearch(T*A, T const& e, Rank lo, Rank hi){
while (1 < hi - lo){//每步迭代仅需做一次比较判断,有两个分支;成功查找不能提前终止
Rank mi = (lo + hi) >> 1;//以中点为轴点
(e < A[mi]) ? hi = mi : lo = mi;//经比较后确定深入[lo,mi)或者[mi,hi)
}//出口时hi= lo +1,查找区间仅含有一个元素A[lo]
return(e == A[lo]) ? lo : -1;//查找成功时返回对应的秩,否则返回-1
}//有多个命中的元素时,不能保证返回秩最大者,失败时简单返回-1,不能确定失败的位置
*/
//////////////////////////////////////////////////////////////////////////////////////
//二分查找算法(版本C)
template
static Rank binSearch(T* A, T const& e, Rank lo, Rank hi){
while (lo < hi){//每步迭代仅需做一次比较判断,有两个分支;成功查找不能提前终止
Rank mi = (lo + hi) >> 1;//以中点为轴点
(e < A[mi]) ? hi = mi : lo = mi + 1;//经过比较后确定[lo,mi)或(mi,hi)查找
}
return --lo;//循环结束时,lo为大于e的元素的最小秩,故lo-1为不大于e的元素的最大秩
}//有多个命中元素时,总能保证返回秩最大者;查找失败时,能够返回失败的位置
#endif // !VECTOR_H
fib.h
#ifndef FIB_H
#define FIB_H
class Fib{//Fibonacci数列类
private:
int f, g;//f = fib(k-1), g = fib(k).均为int型,很快就会数值溢出
public:
Fib(int n){//初始化为不小于n的最小Fibonacci项
f = 1; g = 0; while (g < n) next();
}
int get(){ return g; }//获取当前Fibonacci
int next(){ g += f; f = g - f; return g; }//转至下一项Fibonacci
int prev(){ f = g - f; g -= f; return g; }//转至上一项Fibonacci
};
#endif // !FIB_H对vector的使用将会在以后的stack栈的扩展和queue的扩展时再做介绍
