VI-Big O
Please indicate the source: http://blog.csdn.net/gaoxiangnumber1
Welcome to my github: https://github.com/gaoxiangnumber1
- Big O time is the language and metric we use to describe the efficiency of algorithms.
Time Complexity
Big O, Big Theta, and Big Omega
- O(big O): Big O describes an upper bound on the time. An algorithm that prints all the values in an array could be described as O(N), but it could also be described as any runtime bigger than O(N), such as O(N2), O(N3), or O(2N). The algorithm is at least as fast as each of these; therefore they are upper bounds on the runtime.
- Ω(big omega): Ω is the lower bound. Printing the values in an array is O(N) as well as O(log N) and O(1). It won’t be faster than those runtimes.
- Θ(big theta): Θ means both O and Ω. An algorithm is Θ(N) if it is both O(N) and Ω(N). Θ gives a tight bound on runtime.
- In interviews, people seem to have merged Θ and O together. Industry’s meaning of big O is closer to what academics mean by Θ, so it would be seen as incorrect to describe printing an array as O(N2). Industry would just say this is O(N). We use big O in the way that industry tends to use it: offer the tightest description of the runtime.
Best Case, Worst Case, and Expected Case
- We can describe runtime for an algorithm in three ways. E.g., quick sort picks a random element as a “pivot” and then swaps values in the array such that the elements less than pivot appear before elements greater than pivot. Then it recursively sorts the left and right sides using a similar process.
1.Best Case: If all elements are equal, then quick sort will, on average, traverse through the array once. This is O(N).
2.Worst Case: When the pivot is repeatedly the biggest element in the array(this can happen if the pivot is chosen to be the first element in the subarray and the array is sorted in reverse order), recursion doesn’t divide the array in half and recurse on each half. It just shrinks the subarray by one element. This will degenerate to an O(N2) runtime.
3.Expected Case: Sometimes the pivot will be very low or very high, but it won’t happen over and over again. We can expect a runtime of O(N log N). - The best case time complexity is not a very useful concept. For most algorithms, the worst case and the expected case are the same. Sometimes they’re different and we need to describe both of the runtimes.
- What is the relationship between best/worst/expected case and Big O/theta/omega?
There is no particular relationship between the concepts.
- Best, worst, and expected cases describe the big O(or big theta) time for particular inputs or scenarios.
- Big O, big omega, and big theta describe the upper, lower, and tight bounds for the runtime.
Space Complexity
- If we need to create an array of size n, this will require O(n) space.
If we need a two-dimensional array of size n*n, this will require O(n2) space. - Stack space in recursive calls also counts. Following code takes O(n) time and O(n) space.
int sum(int n) /*Ex 1.*/
{
if (n <= 0)
{
return 0;
}
return n + sum(n-1);
}- Each call adds a level to the stack.
1 sum(4)
2 -> sum(3)
3 -> sum(2)
4 -> sum(l)
5 -> sum(0)- Each of these calls is added to the call stack and takes up actual memory.
- Have n calls total doesn’t mean it takes O(n) space. The below function adds adjacent elements between 0 and n:
int pairSumSequence(int n) /* Ex 2.*/
{
int sum = 0;
for (int i= 0; i < n; i++)
{
sum += pairSum(i, i + 1);
}
return sum;
}
int pairSum(int a, int b)
{
return a + b;
}- There will be roughly O(n) calls to pairSum, but those calls do not exist simultaneously on the call stack, so it needs O(1) space.
Drop the Constants
- O(N) code may run faster than O(1) code for specific inputs. Big O just describes the rate of increase. For this reason, we drop the constants in runtime. An algorithm that one describes as O(2N) is actually O(N).
Drop the Non-Dominant Terms
- You should drop the non-dominant terms.
O(N2 + N) becomes O(N2).
O(N + log N) becomes O(N).
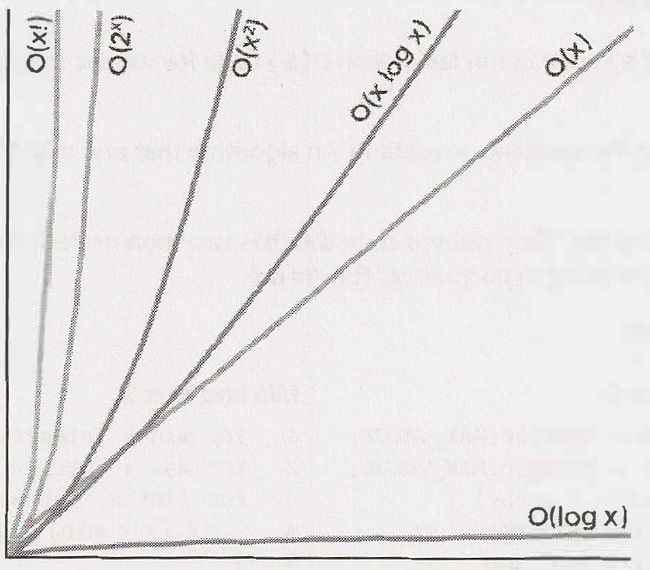
O(5*2N + 1000N100) becomes O(2N). - The following graph depicts the rate of increase for common big O times.
Multi-Part Algorithms: Add vs. Multiply
- Suppose you have an algorithm that has two steps. When do you multiply the runtimes and when do you add them?
// Add the Runtimes: O(A + B)
for(int a : arrA)
{
print(a);
}
for(int b : arrB)
{
print(b);
}
// Multiply the Runtimes: O(A* B)
for(int a : arrA)
{
for(int b : arrB)
{
print(a + ',' + b);
}
}- If your algorithm is in the form “do this, then, when you’re all done, do that”, then you add the runtimes.
If your algorithm is in the form “do this for each time you do that”, then you multiply the runtimes.
Amortized Time(平摊时间)
- A Vector is implemented with an array. When the array hits capacity, the Vector class will create a new array with double the capacity and copy all the elements over to the new array.
- What’s the runtime of insertion?
- When the array is full: If the array contains N elements, then inserting a new element will take O(N) time. You will have to create a new array of size 2N and then copy N elements over. But this doesn’t happen often.
- The majority of the time insertion will be in O(l) time.
- Amortized time takes both into account and it allows us to describe that, this worst case happens every once in a while. But once it happens, it won’t happen again for so long that the cost is “amortized”. In this case, what is the amortized time?
- As we insert elements, we double the capacity when the size of the array is a power of 2. So after X elements, we double the capacity at array sizes 1, 2, 4, 8, 16, … , X. That doubling takes, respectively, 1, 2, 4, 8, 16, 32, 64, … , X copies.
- What is the sum of 1 + 2 + 4 + 8 + 16 + … + X? Read right to left, it starts with X and halves until it gets to 1. What then is the sum of X + X/2 + X/4 + X/8 + … + 1 ? This is roughly 2X.
So, X insertions take O(2X) time. The amortized time for each insertion is O(1).
Log N Runtimes
- Binary search: look for an example x in an N-element sorted array. First compare x to the midpoint of the array.
- If x == middle, then return.
- If x < middle, then search on the left side of the array.
- If x > middle, then search on the right side of the array.
search 9 within {1, 5, 8, 9, 11, 13, 15, 19, 21}
compare 9 to 11 -> smaller.
search 9 within {1, 5, 8, 9, 11}
compare 9 to 8 -> bigger
search 9 within {9, 11}
compare 9 to 9
return- We start with an N-element array to search. After one step, we’re down to N/2 elements. One more step, and we’re down to N/4 elements. We stop when we either find the value or we’re down to just one element.
- The total runtime is then a matter of how many steps(dividing N by 2 each time) we can take until N becomes 1.
What is k in the expression 2k = N? This is what log expresses.
log2N = k -> 2k = N. - When you see a problem where the number of elements in the problem space gets halved each time, that will likely be a O(logN) runtime.
- This is the same reason why finding an element in a balanced binary search tree is O(log N). With each comparison, we go either left or right. Half the nodes are on each side, so we cut the problem space in half each time.
Bases of Logs(page 630)
- Suppose we have something in log2(log base 2). How do we convert that to log10? That is, what’s the relationship between logbk and logxk?
- Assume c = logbk and y = logxk.
logbk = c -> bc = k // This is the definition of log.
logx(bc) = logxk // Take log of both sides of bc = k.
c*logxb = logxk // Rules of logs. You can move out the exponents.
c = logbk = logxk / logxb // Dividing above expression and substituting c.
Therefore, if we want to convert log2p to log10, we just do this: log10p = log2p / log210 - Takeaway: Logs of different bases are only off by a constant factor. For this reason, we largely ignore what the base of a log within a big O expression. It doesn’t matter since we drop constants anyway.
Recursive Runtimes
- What’s the runtime of this code?
int f(int n)
{
if (n <= 1)
{
return 1;
}
return f(n - 1) + f(n - 1);
}Suppose we call f(4). This calls f(3) twice. Each of those calls to f(3) calls f(2), until we get down to f(1).
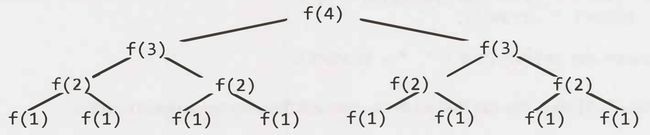
The tree will have depth N. Each node(i.e., function call) has two children. Therefore, each level will have twice as many calls as the one above it. There will be 2 + 21 + 22 + 23 + 24 + . . + 2N = (2N+1 - 1) nodes.
- Remember this pattern: When have a recursive function that makes multiple calls, the runtime will often look like O(branches depth), where branches is the number of times each recursive call branches. In this case, this gives O(2N).
- The base of a log doesn’t matter for big O since logs of different bases are only different by a constant factor. But the base of an exponent does matter. Compare 2n and 8n. If you expand 8n, you get(23)n, which equals 23n, which equals 22n * 2n. 8n and 2n are different by a factor of 22n. That is not a constant factor!
- The space complexity of this algorithm is O(N). Although we have O(2N) nodes in the tree total, only O(N) exist at any given time. Therefore, we only need O(N) memory available.
Examples and Exercises
Example 1
void foo(int[] array)
{
int sum = 0;
int product = 1;
for (int i= 0; i < array.length; i++)
{
sum += array[i];
}
for (int i= 0; i < array.length; i++)
{
product *= array[i];
}
System.out.println(sum + ", " + product);
}- This will take O(N) time. The fact that we iterate through the array twice doesn’t matter.
Example 2
void printPairs(int[] array)
{
for (int i= 0; i < array.length; i++)
{
for (int j = 0; j < array.length; j++)
{
System.out.println(array[i] + "," + array[j]);
}
}
}- The inner for loop has O(N) iterations and it is called N times. The runtime is O(N2).
Example 3
void printUnorderedPairs(int[] array)
{
for (int i= 0; i < array.length; i++)
{
for (int j = i + 1; j < array.length; j++)
{
System.out.println(array[i] + "," + array[j]);
}
}
}- The first time through j runs for N-1 steps. The second time, it’s N-2 steps. Then N-3 steps. And so on. Therefore, the number of steps total is: (N-1) + (N-2) + (N-3) + … + 2 + 1 = 1 + 2 + 3 + … + N-1 = N(N-1)/2, so the runtime is O(N2).
Example 4
void printUnorderedPairs(int[] arrayA, int[] arrayB)
{
for (int i= 0; i < arrayA.length; i++)
{
for (int j = 0; j < arrayB.length; j++)
{
if (arrayA[i] < arrayB[j])
{
System.out.println(arrayA[i] + "," + arrayB[j]);
}
}
}
}- We can break up this analysis. The if statement within j’s for loop is O(1) time since it’s a sequence of constant-time statements. We now have this:
void printUnorderedPairs(int[] arrayA, int[] arrayB)
{
for (int i= 0; i < arrayA.length; i++)
{
for (int j = 0; j < arrayB.length; j++)
{
/* O(1) work */
}
}
}- For each element of arrayA, the inner for loop goes through b iterations, where b = arrayB.length. If a = arrayA.length, then the runtime is O(a*b). O(N2) is wrong because there are two different inputs, both matter.
Example 5
void printUnorderedPairs(int[] arrayA, int[] arrayB)
{
for (int i = 0; i < arrayA.length; i++)
{
for (int j = 0; j < arrayB.length; j++)
{
for (int k= 0; k < 100000; k++)
{
System.out.println(arrayA[i] + "," + arrayB[j]);
}
}
}
}- Nothing really changes here. 100000 units of work is still constant, so the runtime is O(ab).
Example 6
void reverse(int[] array)
{
for (int i= 0; i <array.length/2; i++)
{
int other= array.length - i - 1;
int temp= array[i];
array[i] = array[other];
array[other] = temp;
}
}- This algorithm runs in O(N) time. The fact that it only goes through half of the array(in terms of iterations) does not impact the big O time.
Example 7
- Which of the following are equivalent to O(N)? Why?
- O(N + P), where P < N/2
- O(2N)
- O(N + log N)
- O(N + M)
-
- If P < N/2, then N is the dominant term so we can drop O(P).
- O(2N) is O(N) since we drop constants.
- O(N) dominates O(log N),so we can drop the O(log N).
- There is no established relationship between N and M, so we have to keep both variables.
Example 8
- An algorithm that took in an array of strings, sorted each string, and then sorted the full array.
Incorrect runtime: Sorting each string is O(N log N) and we have to do this for each string, so that’s O(N*N log N). We also have to sort this array, so that’s an additional O(N log N). Therefore, the total runtime is O(N2*log N + N log N), which is O(N2 log N). - The problem is that we use N in two different ways.
- In one case, it’s the length of the string(which string?).
- In another case, it’s the length of the array.
- In interviews, you can prevent this error by either not using the variable “N” at all, or by only using it when there is no ambiguity as to what N represents. You shouldn’t use a and b here, or m and n. It’s too easy to forget which is which and mix them up.
- You should define new terms and use names that are logical.
- Let s be the length of the longest string. Let a be the length of the array.
- Sorting one string is O(s log s) and there are total a strings, so that’s O(a * s log s).
- Now we should sort all the strings. We should take into account that we need to compare the strings. Each string comparison takes O(s) time. There are O(a log a) comparisons, therefore this will take O(s * a log a) time.
- Add up two parts and get O(a*s(log a + log s)). There is no way to reduce it further.
Example 9
- The following code sums the values of all the nodes in a balanced binary search tree.
int sum(Node node)
{
if (node == null)
{
return 0;
}
return sum(node.left) + node.value + sum(node.right);
}- What It Means?
This code touches each node in the tree once and does a constant time amount of work with each “touch”(excluding the recursive calls). Therefore, the runtime will be linear in terms of the number of nodes. If there are N nodes, then the runtime is O(N). - Recursive Pattern
- The runtime of a recursive function with multiple branches is typically O(branches depth). There are two branches at each call, so we’re looking at O(2depth).
- Since the tree is a balanced binary search tree, if there are N total nodes, then depth is roughly log2N. So we get O(2log2N). Therefore, the runtime of this code is O(N), where N is the number of nodes.
Example 10
- The following method checks if a number is prime by checking for divisibility on numbers less than it. It only needs to go up to the square root of n because if n is divisible by a number greater than its square root then it’s divisible by something smaller than it. E.g., while 33 is divisible by 11(which is greater than the square root of 33), the counterpart to 11 is 3(3 * 11 = 33). 33 will have already been eliminated as a prime number by 3.
boolean isPrime(int n)
{
for (int x = 2; x * x <= n; x++)
{
if (n % X == 0)
{
return false;
}
}
return true;
}- The work inside the for loop is constant, we just need to know how many iterations the for loop goes through in the worst case. The for loop start when x = 2 and end when x*x >= n. This runs in O(√n) time.
Example 11
- The following code computes n!(n factorial). What is its time complexity?
int factorial(int n)
{
if (n < 0)
return -1;
else if (n == 0)
return 1;
else
return n * factorial(n - 1);
}- This is a straight recursion from n to n -1 to n - 2 down to 1. It will take O(n) time.
Example 12(Need Reread!!!)
- This code counts all permutations of a string.
void permutation(String str)
{
permutation(str, "");
}
void permutation(String str, String prefix)
{
if (str.length() == 0)
{
10 System.out.println(prefix);
}
else
{
14 for (int i= 0; i < str.length(); i++)
15 {
16 String rem = str.substring(0, i) + str.substring(i + 1);
17 permutation(rem, prefix + str.charAt(i));
18 }
}
}- We can think about this by looking at how many times permutation gets called and how long each call takes. We’ll aim for getting as tight of an upper bound as possible.
- How many times does permutation get called in its base case?
If we were to generate a permutation, then we would need to pick characters for each “slot”. Suppose we had 7 characters in the string. In the first slot, we have 7 choices. Once we pick the letter there, we have 6 choices for the next slot. Then 5 choices for the next slot, and so on. Therefore, the total number of options is 7 * 6 * 5 * 4 * 3 * 2 * 1, which is expressed as 7!(7 factorial). This tells us that there are n! permutations. Therefore, permutation is called n! times in its base case(when prefix is the full permutation). - How many times does permutation get called before its base case?
We also need to consider how many times lines 14 through 18 are hit. Picture a large call tree representing all the calls. There are n! leaves, as shown above. Each leaf is attached to a path of length n. Therefore, we know there will be no more than n * n! nodes(function calls) in this tree. - How long does each function call take?
Executing line 10 takes O(n) time since each character needs to be printed. Line 16 and line 17 also take O(n) time combined, due to the string concatenation. Note that the sum of the lengths of rem, prefix,and str.charAt(i) will always be n. Each node in our call tree therefore corresponds to O(n) work. - What is the total runtime?
Since we are calling permutation O(n * n!) times(as an upper bound), and each one takes O(n) time, the total runtime will not exceed O(n2 * n !) .
Example 13
- The following code computes the Nth Fibonacci number.
int fib(int n)
{
if (n <= 0) return 0;
else if (n == 1) return 1;
return fib(n - 1) + fib(n - 2);
}- We can use the pattern for recursive calls: O(branches depth). There are 2 branches per call, and we go as deep as N, therefore the runtime is O(2N).
- Through complicated math, the actually time is closer to O(1.6N). The reason is that at the bottom of the call stack, there is sometimes only one call. It turns out that a lot of the nodes are at the bottom, so this single versus double call actually makes a difference. Saying O(2N) would suffice for an interview and it is technically correct(big theta).
Example 14
- The following code prints all Fibonacci numbers from 0 to n.
void allFib(int n)
{
for (int i= 0; i < n; i++)
{
System.out.println(i + ": "+ fib(i));
}
}
int fib(int n)
{
if (n <= 0) return 0;
else if (n == 1) return 1;
return fib(n - 1) + fib(n - 2);
}- Wrong: fib(n) takes O(2n) time and it’s called n times, then it’s O(n*2n).
The error is that n is changing. fib(n) takes O(2n) time, but it matters what that value of n is. - The total amount of work is 21 + 22 + 23 + 24 + … + 2n = 2n+1. Therefore, the runtime to compute the first n Fibonacci numbers is still O(2n).
Example 15
- The following code prints all Fibonacci numbers from 0 to n. It stores(i.e., caches) previously computed values in an integer array. If it has already been computed, it just returns the cache. What is its runtime?
void allFib(int n)
{
int[] memo = new int[n + 1];
for (int i= 0; i < n; i++)
{
System.out.println(i + ": "+ fib(i, memo));
}
}
int fib(int n, int[] memo)
{
if (n <= 0) return 0;
else if (n == 1) return 1;
else if (memo[n] > 0) return memo[n];
memo[n] = fib(n - 1, memo) + fib(n - 2, memo);
return memo[n];
}- Let’s walk through what this algorithm does.
fib(l) -> return 1
fib(2)
fib(l) -> return 1
fib(0) -> return 0
store 1 at memo[2]
fib(3)
fib(2) -> lookup memo[2] -> return 1
fib(l) -> return 1
store 2 at memo[3]
fib(4)
fib(3) -> lookup memo[3] -> return 2
fib(2) -> lookup memo[2] -> return 1
store 3 at memo[4]
fib(5)
fib(4) -> lookup memo[4] -> return 3
fib(3) -> lookup memo[3] -> return 2
store 5 at memo[S]- At each call to fib(i), we have already computed and stored the values for fib(i-1) and fib(i-2). We just look up those values, sum them, store the new result, and return. This takes a constant amount of time. We’re doing a constant amount of work N times, so this is O(n) time.
- This technique, called memoization, is a very common one to optimize exponential time recursive algorithms.
Example 16
- The following function prints the powers of 2 from 1 through n(inclusive). For example, if n is 4, it would print 1, 2, and 4. What is its runtime?
int powersof2(int n)
{
if (n < 1)
{
return 0;
}
else if (n == 1)
{
System.out.println(l);
return 1;
}
else
{
int prev = powersof2(n / 2);
int curr = prev * 2;
System.out.println(curr);
return curr;
}
}- What It Means?
Each call to powersof2 results in exactly one number being printed and returned(excluding what happens in the recursive calls). It prints all the powers of 2 between 1 and n. Therefore, the number of times the function is called(which will be its runtime) must equal the number of powers of 2 between 1 and n. There are log N powers of 2 between 1 and n. Therefore, the runtime is O(log n).
Additional Problems
VI.1
The following code computes the product of a and b. What is its runtime?
int product(int a, int b)
{
int sum = 0;
for (int i= 0; i < b; i++)
{
sum += a;
}
return sum;
}- O(b). The for loop iterates through b.
VI.2
The following code computes ab. What is its runtime?
int power(int a, int b)
{
if (b < 0)
return 0; // error
else if (b == 0)
return 1;
else
return a * power(a, b - 1);
}- O(b). The recursive code iterates through b calls, since it subtracts one at each level.
VI.3
The following code computes a % b. What is its runtime?
int mod(int a, int b)
{
if (b <= 0)
{
return -1;
}
int div = a / b;
return a - div *b;
}- O(1). It does a constant amount of work.
VI.4
The following code performs integer division. What is its runtime(assume a and b are both positive)?
int div(int a, int b)
{
int count = 0;
int sum = b;
while (sum <= a)
{
sum += b;
count++;
}
return count;
}- O(a/b). The variable count will eventually equal a/b. The while loop iterates count times. Therefore, it iterates a/b times.
VI.5
The following code computes the [integer] square root of a number. If the number is not a perfect square(there is no integer square root), then it returns -1. It does this by successive guessing. If n is 100, it first guesses 50. Too high? Try something lower-halfway between 1 and 50. What is its runtime?
int sqrt(int n)
{
return sqrt_helper(n, 1, n);
}
int sqrt_helper(int n, int min, int max)
{
if (max < min) return -1; // no square root
int guess = (min + max) / 2;
if (guess * guess == n) // found it!
{
return guess;
}
else if (guess * guess < n) // too low
{
return sqrt_helper(n, guess + 1, max); // try higher
}
else // too high
{
return sqrt_helper(n, min, guess - l); // try lower
}
}- O(log n). This algorithm is doing a binary search to find the square root.
VI.6
The following code computes the [integer] square root of a number. If the number is not a perfect square(there is no integer square root), then it returns -1. It does this by trying increasingly large numbers until it finds the right value(or is too high). What is its runtime?
int sqrt(int n)
{
for (int guess = 1; guess * guess <= n; guess++)
{
if (guess * guess == n)
{
return guess;
}
}
return -1;
}- O(sqrt(n)).
VI.7
If a binary search tree is not balanced, how long might it take(worst case) to find an element in it?
- O(n), where n is the number of nodes in the tree. The max time to find an element is the depth tree. The tree could be a straight list downwards and have depth n.
VI.8
Looking for a specific value in a binary tree, but the tree is not a binary search tree. What is the time complexity of this?
- O(n). Without any ordering property on the nodes, we might have to search through all the nodes.
VI.9
The appendToNew method appends a value to an array by creating a new, longer array and returning this longer array. You’ve used the appendToNew method to create a copyArray function that repeatedly calls appendToNew. How long does copying an array take?
int[] copyArray(int[] array)
{
int[] copy= new int[0];
for (int value : array)
{
copy= appendToNew(copy, value);
}
return copy;
}
int[] appendToNew(int[] array, int value)
{
// copy all elements over to new array
int[] bigger= new int[array.length + 1];
for (int i= 0; i < array.length; i++)
{
bigger[i] = array[i];
}
// add new element
bigger[bigger.length - 1] = value;
return bigger;
}- O(n2), where n is the number of elements in the array. The first call takes 1 copy. The second call takes 2 copies. The third call takes 3 copies. And so on. The total time will be the sum of 1 through n,which is O(n2).
VI.10
The following code sums the digits in a number. What is its big O time?
int sumDigits(int n)
{
int sum = 0;
while (n > 0)
{
sum += n % 10;
n /= 10;
}
return sum;
}- O(log n). The runtime will be the number of digits in the number. A number with d digits can have a value up to 10d. If n = 10d, then d = log n. Therefore, the runtime is 0(log n).
VI.11
The following code prints all strings of length k where the characters are in sorted order. It does this by generating all strings of length k and then checking if each is sorted. What is its runtime?
int numChars = 26;
void printSortedStrings(int remaining)
{
printSortedStrings(remaining, "");
}
void printSortedStrings(int remaining, String prefix)
{
if (remaining== 0)
{
if (isinOrder(prefix))
{
System.out.println(prefix);
}
}
else
{
for (int i= 0; i < numchars; i++)
{
char c = ithletter(i);
printSortedStrings(remaining - 1, prefix + c);
}
}
}
boolean isinOrder(String s)
{
for (int i= 1; i < s.length(); i++)
{
int prev = ithLetter(s.charAt(i - 1));
int curr = ithLetter(s.charAt(i));
if (prev > curr)
{
return false;
}
}
return true;
}
char ithLetter(int i)
{
return (char) (((int) 'a') + i);
}- O(k*ck), where k is the length of the string and c is the number of characters in the alphabet. It takes O(ck) time to generate each string. Then, we need to check that each of these is sorted, which takes O(k) time.
VI.12
The following code computes the intersection(the number of elements in common) of two arrays. It assumes that neither array has duplicates. It computes the intersection by sorting one array(array b) and then iterating through array a checking(via binary search) if each value is in b. What is its runtime?
int intersection(int[] a, int[] b)
{
mergesort(b);
int intersect = 0;
for (int x : a)
{
if (binarySearch(b, x) >= 0)
{
intersect++;
}
}
return intersect;
}- O(b log b + a log b). First, we have to sort array b, which takes O(b log b)time.Then, for each element in a, we do binary search in O(log b) time. The second part takes O(a log b) time.
Please indicate the source: http://blog.csdn.net/gaoxiangnumber1
Welcome to my github: https://github.com/gaoxiangnumber1