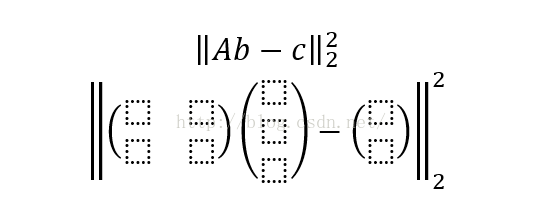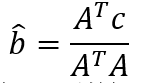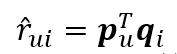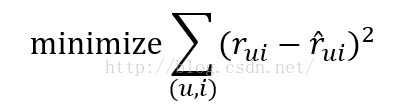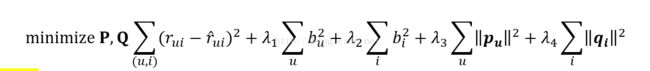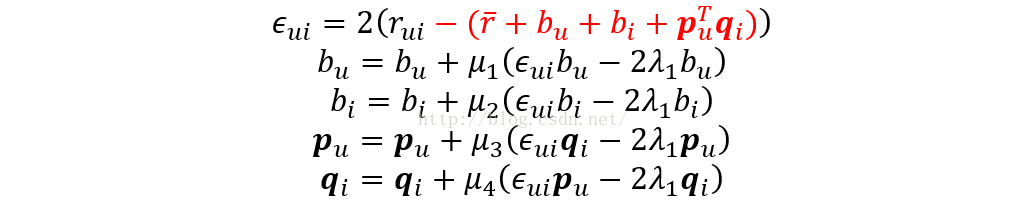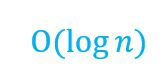电影推荐系统设计思路（简单易懂的算法理解）

以下是我在澳洲留学期间设计的一个电影推荐系统的设计思路，因为我觉得比较有趣，所以放出来也算是一个怀念

本文理论主要参考 Networked Life: 20 Questions and Answers  以及 UNSW COMP9318课程

http://www.handbook.unsw.edu.au/undergraduate/courses/2013/COMP9318.html
http://download.csdn.net/detail/nibudong124/8277417

——————————————————————————————————————————————————————

Method of measuring the quality recommendation system

算法的分类属于collaborative filtering

–David Goldbery1992

 

测试算法效果的方法：Root Mean Squared Error (RMSE)

Basic model

Matrix R Movies * Users 通常电影推荐系统问题使用这样的抽象方法

Sparse matrix 其特征是一个稀疏矩阵

 

组成算法1：

Baseline predictor through least squares

 

 is the average value of allratings. 是所有rating的平均值

the similarities amongusers and movies are not just a statistical fact

i.e. bi 是电影i的特征fact概念类似电影的受欢迎度

      bu 是用户u的特征fact概念类似用户的严格程度

类似的意思是无法用语言表述，是一个抽象的概念

 

我的目标是：

 

解决方法

如果只有bu bi这两个线性的fact的话，最常见解决方案是用linear least squares如课本Baseline predictor through least squares副标题描述的那样解决：

这里解决方案意思是：寻找的最小值，就是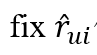使函数收敛，至于函数为什么有最小值数学证明也在课本。

A is C´(N+M)

Solving linear least squares 下面的式子只是上面式子的变形，课本上有详细变形过程

but it is not linear now但是通过这个方法解决问题到这一步已经不是像前面两个fact那样线性的了

 

 

 

 

组成算法2：

因为用户和电影之间不是简单的线性关系如上面fact bu 和bi本省相对独立

user and movies have somelow-dimensional structures hidden in the data. 而是隐藏着一些低维度的相互关系，概念类似于A给有暴力成分的恐怖片分很高，但是给搞笑恐怖片分很低，虽然都是恐怖片，所以无法通过单一的bi分类

所以有

 

Latent factor method:matrix factorization and alternating projection (projections onto convex sets)

convex sets的意思是凸函数，这种函数类型保证了收敛

 

matrix factorization with factor equals to 2

上图是一个维度为2的 matrix factorization

 

for each user u, p_u is a f-dimensional vectorfor the user’s taste to movie. 用户对电影的品味

for each movie i, q_i is a f-dimensional vectorfor the movie’s appeal to user.电影对用户的吸引力

for each p and q, f is the number of the factors. f在这种问题里叫做factor

 

下面一句话描述如何选取合理地f值，这句话是课本的原文，我在下面程序设计部分有具体实例

By picking a f value sothat f(N + M) is about the same as the number of entries in the large, sparsematrix R.

这种算法的表达式是：

The inner product betweenthese two vectors,.

 

initialize every cell ofthe P and Q Matrices as following

pq的初始值这样选因为要pq要内积所以有根号，我们希望只用初始值算出来的矩阵R约等于平均分

b is continuous uniform distribution between [-0.5, 0.5]       

b是均匀分布的

 

Neighborhood method: similarity measure and weighted prediction

我们实际上是要算真是距离：Euclidean space,and the cosine of their angles

 

时间复杂度O（n）

 

 

 

 

最终算法：

 

目标一样是minimize RMSE

解决overfitting问题：since least squares solutions often have over fitting problem

so need regularization 因为上面两个算法都有overfitting问题所以在这里一次性讲，当然也可以分开两次在上面的两个算法里面讲

using Tikhonovregularization现有的例子都在用这个人得算法来regularization

 

 取值问题where  is the regularization parameter

// 0.01 in comp9318

 reason:http://spark.apache.org/docs/latest/mllib-collaborative-filtering.html

上面链接说下面引用的那篇文章研究表明 It makeslambda less dependent on the scale of the dataset.

所以我们去一个最优值0.01

(Zhou et al., 2008)

Zhou, Y., Wilkinson, D.,Schreiber, Rweilezhi. and Pan, R. (2008).Large-Scale Parallel Collaborative Filtering for the NetflixPrize. Algorithmic Aspects inInformation and Management. [online] San Jose: Springer, pp.337-348. Availableat: http://link.springer.com/content/pdf/10.1007%2F978-3-540-68880-8.pdf [Accessed21 Nov. 2015].

 

 

为了达到最小值，我们可以用gd或者sgd让函数收敛

gd和sgd唯一的不同就是gd是每一次收敛计算都遍历所有点然后取速度最快的，sgd是每次随机取，虽然不一定是最快的收敛方向，但是sgd计算效率大大提升

SGD Algorithm

算法思想

每次随机从所有已知rating中选择一个（电影i，用户u）的组合然后刷新以下各值

 

 取值问题where  is the learning rate

// 0.001 in comp9318

原文说这个值非常难取，最好的办法是动态判断函数的收敛程度动态减小该值，可以确认的是这个值一定要足够小才能确保函数的收敛，所以我们（包括上面那个文章的作者和王伟）认为在0.001是一个足够小的值。以上总结是从下面那篇文章看到的

(Bottom,2012)

Bottom,L. (2012). StochasticGradient Descent Tricks. Neural Networks: Tricks of the Trade.[online] Seattle: Springer, pp.414-436. Available at:http://link.springer.com/content/pdf/10.1007%2F978-3-642-35289-8.pdf [Accessed21 Nov. 2015].

 

Since this is a nonconvex optimization problem, theconverged point (P*, Q*) may not be globally optimal.由于我们的函数变化了所以不具备了convex特征，所以有一定几率函数被收敛到了局部极小值而不是最小值

 

 

具体程序实现方法using java to implement

选用的数据集信息

using database fromhttp://grouplens.org/

MovieLens isa project from GroupLens research group in the Department of Computer Scienceand Engineering at the University of Minnesota.

from http://grouplens.org/datasets/movielens/

dataset:数据集大小和内容

3883 movies

6040 users

1000209 ratings

5-star scalerating

all from MovieLensusers who joined MovieLens in 2000

 

具体设计5点注意事项

1.函数收敛判断方法

1.最多随机梯度下降1000次

2.每次判断本次与上次的差值是否大于0.1

   如小于，认为已经收敛到局部极小值，跳出循环

 

2.关于p q初始值

 

关于bu bi的初始值

where  is theaverage rating of user u,某用户的rating平均值

           is theaverage rating of movie i.某电影的rating平均值

 

 

3.随机梯度下降“随机”的部分体现方法

we have timestampvalue in the database

timestamp 是唯一的rating识别符

Timestamp is represented in seconds since the epoch as returned by time(2) 这个是网站的原话

Randomly choose fromall timestamp each time (这个代码应该有可以直接调用的包，COMP9318给了个随机读取表)

 

4.关于k的选取

By picking aK value so that K(N + M) is about the same as the number of entries in thelarge, sparse matrix R上面提到过，这里具体举例

N 是用户数量

M是电影数量

So

finalint FACTOR =100;//因为 1000209 / (3883 + 6040) = 100.797

where 100209 is the # of rating record评分数量

 

5.改进速度用rp树Too slow so we have

Random Projection Trees随机投影树

approximate the cosinedistance between vectors (cosine coefficient)

目的是用概率来模拟实际距离，优化计算效率

Gaussian random direction vector U 下文解释了随机投影方向向量为什么是高斯分布

Reason:http://cseweb.ucsd.edu/~dasgupta/papers/randomf.pdf

 

Dasgupta, S. (2000). Experiments with Random Projection. Proceedings of the 16th Conference on Uncertainty inArtificial Intelligence. [online] San Francisco: Morgan Kaufmann PublishersInc, pp.143-151. Available at:http://cseweb.ucsd.edu/~dasgupta/papers/randomf.pdf [Accessed 21 Nov. 2015].

 

用于算两个点在这个向量上投影的距离

Split Rule of RP-Tree

具体实现思路：取当前node values的中位数，小于等于的放左，大于的放右