算法基础:排序(四)——二叉堆、优先队列、堆排序——Python实现
1. 堆 Heap
堆是利用完全二叉树的结构来维护数据的一种的数据结构,因此堆也叫做二叉堆。借助下面这张图可以直观的理解二叉堆的结构和特点:
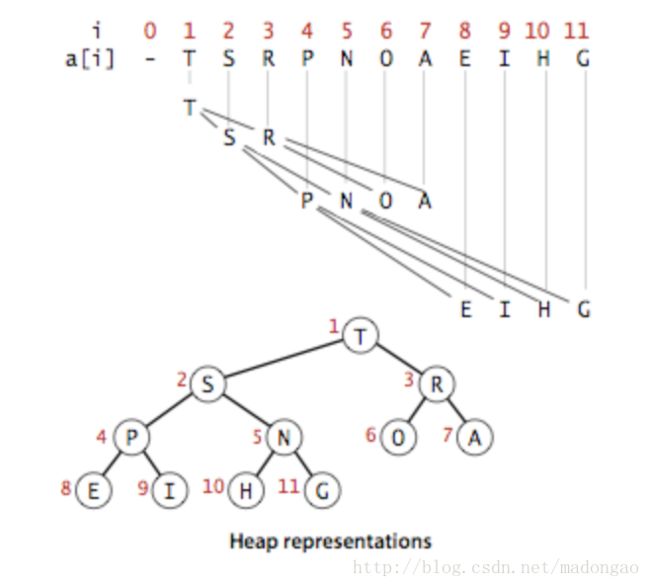
大家不难发现,元素的标号与其父节点的标号n的关系为:
左节点n’=2n,右节点n’=2n+1。
这为我们递归的查找节点提供了路径。
正是因为堆这种二叉树的结构特性,一般利用堆进行一次查找的时间复杂度在O(1)~O(logN)之间,这也正是我们后面利用堆实现优先队列和堆排序降低算法的时间空间成本的原因。
类似于数据结构栈和队列的push和pop两个核心操作,堆的也有两个核心操作:上浮swim和下沉sink,它们是实现堆的有序化的基础,也是实现优先队列的基础。
对于大根堆,我们要求父节点始终大于其两个子节点。但是当我们新插入元素或者是删除(修改)了元素时,堆的这种有序状态可能因为某个节点大于了其父节点而被打破。因此,我们此时需要用swim将大节点与比其小的父节点作交换(插入的新节点,自下而上,类似于上浮),或者是用sink将小的父节点与大的子节点作交换(删除或修改的节点,自上而下,类似于下沉),从而使堆恢复到有序状态。
def __swim(self, k): # k为做上浮节点的标号
while k>1 and self.__less(int(k/2),k):
self.__exchange(int(k/2),k)
k = int(k/2)
def __sink(self, k): # k为做下沉节点的标号
N=self.__size
while 2*k<=N:
j = 2*k
if jand self.__less(j,j+1): # 比较左右子节点,找到大的,准备与当前父节点作比较
j+=1
if not self.__less(k,j): # 当前节点不小于子节点,不做交换
break
self.__exchange(k,j) # exchange
k = j 2. 优先队列 Priority Queue
在实际应用中,我们经常需要处理有序的元素,但很多时候我们不需要他们全部有序,只需要找到最大或者最小的那个值(或者那M个值)。比如操作系统为各进程分配的优先级,当新创建的进程优先级高于其他进程,我们需要将其插入到合适的位置并优先处理最高优先级的进程。
为了从N个进程中,找到优先级最大的M个进程:
如果对所有进程的优先级做排序,那么所需时间成本为O(NlogN),空间成本为O(N)。
如果我们使用线性表构造的初级优先队列,则可以将成本降为O(NM)和O(M)。
但是使用二叉堆实现的优先队列,时间成本仅为O(NlogM),而且在最坏的情况下,也能保证一次插入和删除的时间复杂度为O(logN)。
# 大根堆优先队列,更改为小根堆只需要将元素比较的函数改为more()
class MaxHeapPQ:
def __init__(self):
self.__heap = [None]
self.__size = 0
def __str__(self):
return str(self.__heap[1:])
def insert(self,node):
self.__push(node)
self.__size += 1
self.__swim(self.__size)
def delMax(self):
if self.isEmpty():
print("Empty PQ!")
return
self.__heap[1] = self.__heap[self.__size] # 用最后一个元素替换root
del self.__heap[self.__size]
self.__size -= 1
self.__sink(1)
def changeRoot(self,node):
if self.isEmpty():
self.insert(node)
return
self.__heap[1] = node # 修改root的值
self.__sink(1)
def max(self):
if self.isEmpty():
print("Empty PQ!")
return
return self.__heap[1]
def getSize(self):
return self.__size
def isEmpty(self):
return self.__size <= 0
def __push(self, item):
self.__heap.append(item)
def __less(self, i, j): # 比较heap[i],heap[j]
return self.__heap[i] < self.__heap[j]
def __exchange(self, i, j): # 交换heap[i],heap[j]
self.__heap[i], self.__heap[j] = self.__heap[j], self.__heap[i]
def __swim(self, k): # k为做上浮节点的标号
while k>1 and self.__less(int(k/2),k):
self.__exchange(int(k/2),k)
k = int(k/2)
def __sink(self, k): # k为做下沉节点的标号
N=self.__size
while 2*k<=N:
j = 2*k
if jand self.__less(j,j+1): # 比较左右子节点,找到大的,准备与当前父节点作比较
j+=1
if not self.__less(k,j): # 当前节点不小于子节点,不做交换
break
self.__exchange(k,j) # exchange
k = j 3. 堆排序 HeapSort
观察上图delmax()打印结果的第一列,是不是很神奇的将原数组按从大到小排了序,然而这并不是巧合。想象一下,我们每次取出优先队列的最大值,倒序放入一个新数组中,那么这个数组不就是一个从小到大排序的数组吗。如果我们的优先队列是基于堆实现的,基于这样思想的排序算法就是堆排序。
截取这一段代码很容易理解堆排序的流程:
# 构造堆,从右至左从N/2~1
for i in range(int(N/2),0,-1):
self.__sink(a,i,N) # 对每一个子堆的根节点做sink()
# 堆排序
for i in range(N,1,-1):
#从a[N]到a[2]每次与root交换,max依次放置于a[N]~a[2]
self.__exchange(a,1,i)
#堆大小-1,对新root做sink()
self.__sink(a,1,i-1)首先,我们将需要构造堆。将排序的数组本身构造成为一个堆,这样就无需额外空间。从左至右遍历数组,利用swim()操作,如同连续向优先队列中插入元素一样;或者从右至左从N/2~1对每一个子堆的根节点做sink()递归地建立堆的秩序,这样做更加高效。
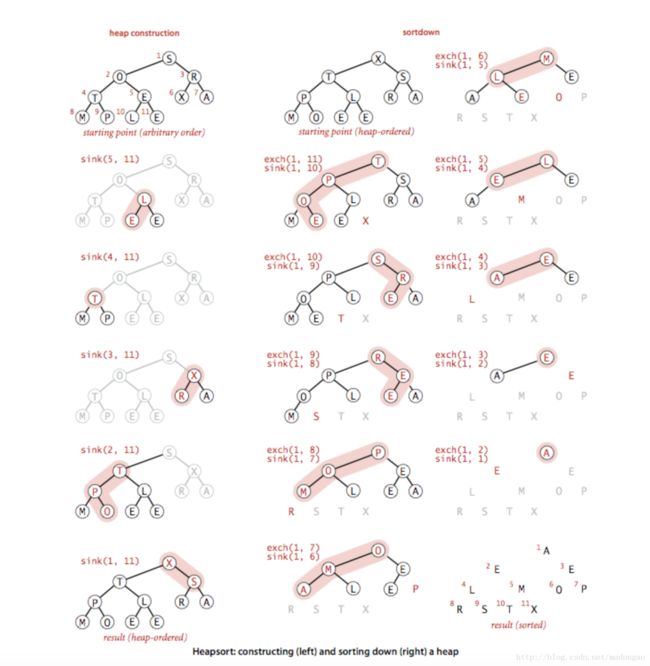
然后,我们进行堆排序。每次对root节点的Max,用最后一个叶子节点替换,此时堆的秩序被打破,我们需要对新的root节点做sink(),将第二大的节点置于root,恢复堆的秩序。再将Max放置于数组的最后,这样相当于每次将root与最后的叶子节点交换,sink()新root重建堆秩序,堆的大小减1。这样从a[N]到a[2]依次从大到小放置完毕所有元素后,便在原地得到了从小到大排序的数组。
堆排序的过程可以参考下图(来自:http://algs4.cs.princeton.edu/24pq/)
class HeapSort:
def sort(self, a):
N = len(a)
a.insert(0, None) # 调整a的标号以方便堆操作
# 构造堆
for i in range(int(N/2),0,-1):
self.__sink(a,i,N)
# 堆排序
for i in range(N,1,-1):
self.__exchange(a,1,i)
self.__sink(a,1,i-1)
a.pop(0)
def __less(self, a, i, j): # 比较heap[i],heap[j]
return a[i] < a[j]
def __exchange(self, a, i, j): # 交换heap[i],heap[j]
a[i],a[j] = a[j], a[i]
def __sink(self, a, k, N): # k为做下沉节点的标号
while 2*k<=N:
j = 2*k
if jand self.__less(a,j,j+1): # 比较左右子节点,找到大的,准备与当前父节点作比较
j+=1
if not self.__less(a,k,j): # 当前节点不小于子节点,不做交换
break
self.__exchange(a,k,j) # exchange
k = j