哈夫曼树详解
一、哈夫曼树的介绍
Huffman Tree,中文名是哈夫曼树或霍夫曼树,它是最优二叉树。
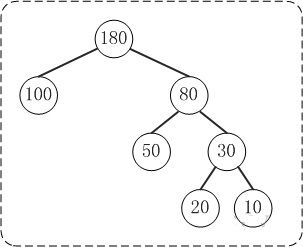
定义:给定n个权值作为n个叶子结点,构造一棵二叉树,若树的带权路径长度达到最小,则这棵树被称为哈夫曼树。 这个定义里面涉及到了几个陌生的概念,下面就是一颗哈夫曼树,我们来看图解答。
(1) 路径和路径长度
定义:在一棵树中,从一个结点往下可以达到的孩子或孙子结点之间的通路,称为路径。通路中分支的数目称为路径长度。若规定根结点的层数为1,则从根结点到第L层结点的路径长度为L-1。 例子:100和80的路径长度是1,50和30的路径长度是2,20和10的路径长度是3。
(2) 结点的权及带权路径长度
定义:若将树中结点赋给一个有着某种含义的数值,则这个数值称为该结点的权。结点的带权路径长度为:从根结点到该结点之间的路径长度与该结点的权的乘积。 例子:节点20的路径长度是3,它的带权路径长度= 路径长度 * 权 = 3 * 20 = 60。
(3) 树的带权路径长度
定义:树的带权路径长度规定为所有叶子结点的带权路径长度之和,记为WPL。 例子:示例中,树的WPL= 1*100 + 2*50 + 3*20 + 3*10 = 100 + 100 + 60 + 30 = 290。
比较下面两棵树
上面的两棵树都是以{10, 20, 50, 100}为叶子节点的树。
左边的树WPL=2*10 + 2*20 + 2*50 + 2*100 = 360 右边的树WPL=290
左边的树WPL > 右边的树的WPL。你也可以计算除上面两种示例之外的情况,但实际上右边的树就是{10,20,50,100}对应的哈夫曼树。至此,应该对哈夫曼树的概念有了一定的了解了,下面看看如何去构造一棵哈夫曼树。
二、哈夫曼树的图文解析
假设有n个权值,则构造出的哈夫曼树有n个叶子结点。 n个权值分别设为 w1、w2、…、wn,哈夫曼树的构造规则为:
1. 将w1、w2、…,wn看成是有n 棵树的森林(每棵树仅有一个结点); 2. 在森林中选出根结点的权值最小的两棵树进行合并,作为一棵新树的左、右子树,且新树的根结点权值为其左、右子树根结点权值之和; 3. 从森林中删除选取的两棵树,并将新树加入森林; 4. 重复(02)、(03)步,直到森林中只剩一棵树为止,该树即为所求得的哈夫曼树。
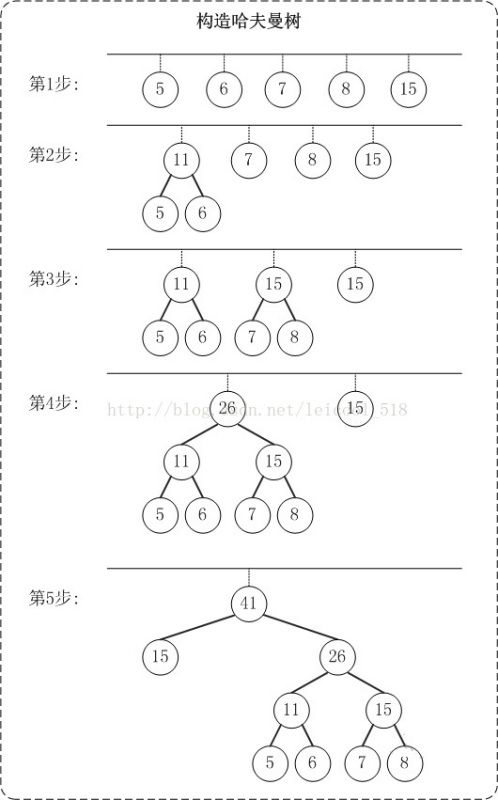
以{5,6,7,8,15}为例,来构造一棵哈夫曼树。
第1步:创建森林,森林包括5棵树,这5棵树的权值分别是5,6,7,8,15。 第2步:在森林中,选择根节点权值最小的两棵树(5和6)来进行合并,将它们作为一颗新树的左右孩子(谁左谁右无关紧要,这里,我们选择较小的作为左孩子),并且新树的权值是左右孩子的权值之和。即,新树的权值是11。 然后,将"树5"和"树6"从森林中删除,并将新的树(树11)添加到森林中。 第3步:在森林中,选择根节点权值最小的两棵树(7和8)来进行合并。得到的新树的权值是15。 然后,将"树7"和"树8"从森林中删除,并将新的树(树15)添加到森林中。 第4步:在森林中,选择根节点权值最小的两棵树(11和15)来进行合并。得到的新树的权值是26。 然后,将"树11"和"树15"从森林中删除,并将新的树(树26)添加到森林中。 第5步:在森林中,选择根节点权值最小的两棵树(15和26)来进行合并。得到的新树的权值是41。 然后,将"树15"和"树26"从森林中删除,并将新的树(树41)添加到森林中。 此时,森林中只有一棵树(树41)。这棵树就是我们需要的哈夫曼树!
三、哈夫曼树的基本操作
哈夫曼树的重点是如何构造哈夫曼树。本文构造哈夫曼时,用到了以前介绍过的"(二叉堆)最小堆"。下面对哈夫曼树进行讲解。
1. 基本定义
[html]
view plain
copy
HuffmanNode是哈夫曼树的节点类。
[html]
view plain
copy
Huffman是哈夫曼树对应的类,它包含了哈夫曼树的根节点和哈夫曼树的相关操作。
2. 构造哈夫曼树
[html]
view plain
copy
首先创建最小堆,然后进入for循环。
每次循环时:
(1) 首先,将最小堆中的最小节点拷贝一份并赋值给left,然后重塑最小堆(将最小节点和后面的节点交换位置,接着将"交换位置后的最小节点"之前的全部元素重新构造成最小堆); (2) 接着,再将最小堆中的最小节点拷贝一份并将其赋值right,然后再次重塑最小堆; (3) 然后,新建节点parent,并将它作为left和right的父节点; (4) 接着,将parent的数据复制给最小堆中的指定节点。
四、哈夫曼树的完整源码
1. 哈夫曼树的节点类(HuffmanNode.java)
[html]
view plain
copy
2. 哈夫曼树的实现文件(Huffman.java)
[html]
view plain
copy
3. 哈夫曼树对应的最小堆(MinHeap.java)
[html]
view plain
copy
4. 哈夫曼树的测试程序(HuffmanTest.java)
[html]
view plain
copy
五个字符:a,b,c,d,e,它们出现的的频率为8,14,10,4,18构造相应的哈夫曼树,求出每个字符的哈夫曼编码:
哈夫曼树:
54
/ \
22 32
/ \ / \
c10 12 b14 e18
/ \
d4 a8哈夫曼编码:
a:011 b:10 c:00 d:010 e:11
今天做题的时候,遇到了一个关于哈夫曼树的题,由于一直不是很明白哈夫曼树的构造过程,所以找了很多资料都不是特别清楚的,直到我遇到了这篇文章,哈哈,在此分享给大家哦!
注意:哈夫曼树并不唯一,但带权路径长度一定是相同的。
(1)8个结点的权值大小如下:
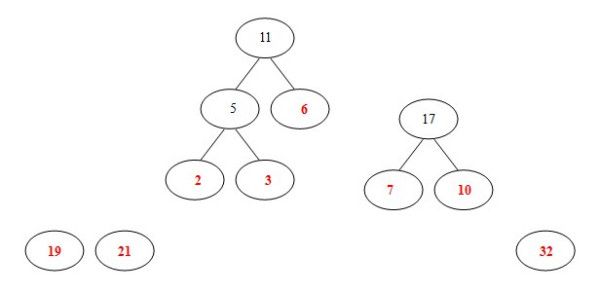
(2)从19,21,2,3,6,7,10,32中选择两个权小结点。选中2,3。同时算出这两个结点的和5。
(3)从19,21,6,7,10,32,5中选出两个权小结点。选中5,6。同时计算出它们的和11。
(4)从19,21,7,10,32,11中选出两个权小结点。选中7,10。同时计算出它们的和17。 (BTW:这时选出的两个数字都不是已经构造好的二叉树里面的结点,所以要另外开一棵二叉树;或者说,如果两个数的和正好是下一步的两个最小数的其中的一个,那么这个树直接往上生长就可以了,如果这两个数的和比较大,不是下一步的两个最小数的其中一个,那么就并列生长。)
(4)从19,21,7,10,32,11中选出两个权小结点。选中7,10。同时计算出它们的和17。
(BTW:这时选出的
两个数字都不是已经构造好的二叉树里面的结点
,所以要另外开一棵二叉树;或者说,
如果两个数的和正好是下一步的两个最小数的其中的一个
,那么这个树直接往上生长就可以了,如果这两个数的和比较大,不是下一步的两个最小数的其中一个,那么就并列生
长。)
(4)从19,21,7,10,32,11中选出两个权小结点。选中7,10。同时计算出它们的和17。 (BTW:这时选出的两个数字都不是已经构造好的二叉树里面的结点,所以要另外开一棵二叉树;或者说,如果两个数的和正好是下一步的两个最小数的其中的一个,那么这个树直接往上生长就可以了,如果这两个数的和比较大,不是下一步的两个最小数的其中一个,那么就并列生长。)
(5)从19,21,32,11,17中选出两个权小结点。选中11,17。同时计算出它们的和28。
(6)从19,21,32,28中选出两个权小结点。选中19,21。同时计算出它们的和40。另起一颗二叉树。
(7)从32,28, 40中选出两个权小结点。选中28,32。同时计算出它们的和60。
(8)从 40, 60中选出两个权小结点。选中40,60。同时计算出它们的和100。 好了,此时哈夫曼树已经构建好了。
这是原作者的链接哦,我觉得还不错呢,大家可以去看看的!
注意:哈夫曼树并不唯一,但带权路径长度一定是相同的。
(1)8个结点的权值大小如下:
(2)从19,21,2,3,6,7,10,32中选择两个权小结点。选中2,3。同时算出这两个结点的和5。
(3)从19,21,6,7,10,32,5中选出两个权小结点。选中5,6。同时计算出它们的和11。
(4)从19,21,7,10,32,11中选出两个权小结点。选中7,10。同时计算出它们的和17。 (BTW:这时选出的两个数字都不是已经构造好的二叉树里面的结点,所以要另外开一棵二叉树;或者说,如果两个数的和正好是下一步的两个最小数的其中的一个,那么这个树直接往上生长就可以了,如果这两个数的和比较大,不是下一步的两个最小数的其中一个,那么就并列生长。)
(4)从19,21,7,10,32,11中选出两个权小结点。选中7,10。同时计算出它们的和17。
(BTW:这时选出的
两个数字都不是已经构造好的二叉树里面的结点
,所以要另外开一棵二叉树;或者说,
如果两个数的和正好是下一步的两个最小数的其中的一个
,那么这个树直接往上生长就可以了,如果这两个数的和比较大,不是下一步的两个最小数的其中一个,那么就并列生
长。)
(4)从19,21,7,10,32,11中选出两个权小结点。选中7,10。同时计算出它们的和17。 (BTW:这时选出的两个数字都不是已经构造好的二叉树里面的结点,所以要另外开一棵二叉树;或者说,如果两个数的和正好是下一步的两个最小数的其中的一个,那么这个树直接往上生长就可以了,如果这两个数的和比较大,不是下一步的两个最小数的其中一个,那么就并列生长。)
(5)从19,21,32,11,17中选出两个权小结点。选中11,17。同时计算出它们的和28。
(6)从19,21,32,28中选出两个权小结点。选中19,21。同时计算出它们的和40。另起一颗二叉树。
(7)从32,28, 40中选出两个权小结点。选中28,32。同时计算出它们的和60。
(8)从 40, 60中选出两个权小结点。选中40,60。同时计算出它们的和100。 好了,此时哈夫曼树已经构建好了。