【BZOJ4539】【Hnoi2016】树 树套树

你萌知道一道题从晚八点调到早一点是什么感觉么？

你萌知道凌晨一点的CQ长什么样子么？

你萌知道TLE或者WA的情况显示成RE对没有数据的小朋友伤害有多大吗？？？

我！知！道！

算了我们来说说Hn的这套题。。。

6道DS。。。

这道是我当时拿道题后第一道yy出标算的题。。。

我也不知道是算树套树还是算分块。。。

主要思想就是把模板树建好之后，每个加入一块树的操作在大树中只加入一个代表节点，代表节点的父亲设置为实际父亲所在块的代表节点（当然实际父亲也要存下来），并处理出大树的倍增数组（LCA用），代表节点与他的父亲的距离设置为代表节点与父亲代表节点之间的真实距离（语文渣见谅）。

当然我们还要拿DFS序和可持久做预处理以便快速查询某棵子树的第k大。。。

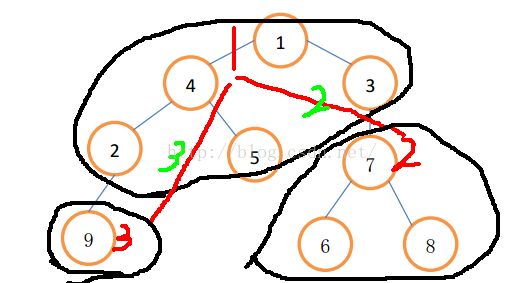
如图，红色数字为代表节点，绿色数字为代表节点与他父亲的距离

对于每次查询，我们先找出两个节点的代表节点以及代表节点的LCA，如果两个实际节点在同一个树块上，直接在模板上求距离即可，否则将两个代表节点跳到LCA，记录沿途的长度，将情况化归为两个实际节点在同一个树块上。

例如，我们要查询5,6之间的距离，当前ans=0

将6跳到当前块的根7 ，ans=1

7跳到实际父亲3，ans=2

3和5在同一块中求得距离3，ans=5

细节多如牛毛。。。

#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
#define maxn 250005
struct edge
{
	int to,d,next;
};
int n,m,q;
namespace Ta
{
	edge e[maxn*10];
	int time,edge_ct,f[maxn],fb[maxn][22],head[maxn],SZ[maxn];
	long long d[maxn],sz[30*maxn];
	int np,rt[maxn],chi[30*maxn][2],tl[maxn],tr[maxn],_tl[maxn];
	void add(int x,int y)
	{
		e[++edge_ct]=(edge){y,1,head[x]}; head[x]=edge_ct;
		return ;
	}
	void BFS()
	{
		queueq; q.push(1);
		memset(d,0,sizeof(d)); d[1]=1;
		int i,j;
		while(!q.empty())
		{
			i=q.front() ; q.pop();
			for(int id=head[i];id;id=e[id].next)
			{
				j=e[id].to; if(d[j])continue;
				d[j]=d[i]+1; f[j]=i; 
				q.push(j);
			}
		}
		return ;
	}
	void makefb()
	{
		for(int i=1;i<=n;i++)fb[i][0]=f[i];
		for(int k=1;k<=20;k++)
		{
			for(int i=1;i<=n;i++)
			{
				fb[i][k]=fb[fb[i][k-1]][k-1];
			}
		}
		return ;
	}
	long long LCA(long long x,long long y)
	{
		if(x==0 || y== 0 )return 0;
		if(d[x]=0;k--)if(d[x]-d[y]>=(1<=0;k--)if(fb[x][k]!=fb[y][k])
		{
			x=fb[x][k]; y=fb[y][k];
		}
		return f[x];
	}
	void build(int &now,int L,int R)
	{
		now=++np; sz[now]=0;
		if(L>=R)
		{
			return ;
		}
		int m=(L+R)>>1;
		build(chi[now][0],L,m);
		build(chi[now][1],m+1,R);
		return ;
	}
	void Insert(int anc,int &now,int L,int R,int x)
	{
		now=++np;
		sz[now]=sz[anc]+1;
		if(L>=R)
		{
			return ;
		}
		int m=(L+R)>>1;
		if(x<=m)
		{
			chi[now][1]=chi[anc][1];
			Insert(chi[anc][0],chi[now][0],L,m,x);
		}
		else
		{
			chi[now][0]=chi[anc][0];
			Insert(chi[anc][1],chi[now][1],m+1,R,x);
		}
		return ;
	}
	void DFS(int now)
	{
		tl[now]=++time; _tl[time]=now; SZ[now]=1;
		for(int id=head[now];id>0;id=e[id].next)if(!tl[e[id].to])
		{
			DFS(e[id].to);
			SZ[now]+=SZ[e[id].to];
		}
		tr[now]=time;
		return ;
	}
	long long Kth(int anc,int now,int L,int R,long long k)
	{
		if(L>=R)
		{
			return L;
		}
		int m=(L+R)>>1;
		long long ct=sz[chi[now][0]]-sz[chi[anc][0]];
		if(k<=ct)
		{
			return Kth(chi[anc][0],chi[now][0],L,m,k);
		}
		else
		{
			return Kth(chi[anc][1],chi[now][1],m+1,R,k-ct);
		}
	}
};
char s[85];int cct;
void out(long long x)
{
	if(!x)
	{
		putchar('0');putchar('\n');return;
	}
	cct=0;
	while(x)
	{
		s[++cct]=x%10+'0'; x=x/10;
	}
	for(int i=cct;i>=1;i--)putchar(s[i]);
	putchar('\n');
	return ;
}
namespace Tb
{

	int np,f[maxn],fb[maxn][22],f_r[maxn],real[maxn];
	long long dis[maxn],d[maxn];

	long long LCA(long long x,long long y)
	{
		if(d[x]=0;k--)if(d[x]-d[y]>=(1<=0;k--)if(fb[x][k]!=fb[y][k])
		{
			x=fb[x][k]; y=fb[y][k];
		}
		return f[x];
	}
	long long a[maxn];
	int a_cnt;
	int Find(long long t)
	{
		int w=lower_bound(a+1,a+1+a_cnt,t)-a;
		return w;
	}
	void makefb(int now)
	{
		fb[now][0]=f[now]; 
		for(int k=1;k<=20;k++)fb[now][k]=fb[fb[now][k-1]][k-1];
		return ;
	}
	void Insert(int x,long long y)
	{
		int z=Find(y);
		np++; f[np]=z; f_r[np]=(long long)(y-a[z-1]); real[np]=x;
		a_cnt++;a[a_cnt]=a[a_cnt-1]+(long long)Ta::SZ[x];
		d[np]=d[z]+1;
		int w=Ta::Kth(Ta::rt[Ta::tl[real[z]]-1],Ta::rt[Ta::tr[real[z]]],0,n+1,f_r[np]);
		dis[np]=dis[z]+(long long)(Ta::d[w]-Ta::d[real[z]]+1);
		makefb(np);
		return ;
	}
	void query(long long x,long long y)
	{
		long long t1=Find(x),t2=Find(y);
		long long id1=(int)(x-a[t1-1]),id2=(int)(y-a[t2-1]);
		
		long long _ida=0;if(Ta::tl[real[t1]]>=1 && Ta::tr[real[t1]]>=0)_ida=Ta::Kth(Ta::rt[Ta::tl[real[t1]]-1],Ta::rt[Ta::tr[real[t1]]],0,n+1,id1);
		long long _idb=0;if(Ta::tl[real[t2]]>=1 && Ta::tr[real[t2]]>=0)_idb=Ta::Kth(Ta::rt[Ta::tl[real[t2]]-1],Ta::rt[Ta::tr[real[t2]]],0,n+1,id2);
		long long t3=LCA(t1,t2);
		
		long long dis1=0,dis2=0,_Ans=0;
		
		if(t1==t2)
		{
			out(Ta::d[_ida]+Ta::d[_idb]-2*Ta::d[Ta::LCA(_ida,_idb)]);
			return ;
		}
		else
		{
			if(t1!=t3 && _ida>=0 && real[t1]>=0)dis1+=Ta::d[_ida]-Ta::d[real[t1]];
			if(t2!=t3 && _idb>=0 && real[t2]>=0)dis2+=Ta::d[_idb]-Ta::d[real[t2]];
			
			if(t1!=t3)
			{
				for(int k=20;k>=0;k--)if(d[t1]-d[t3]>(1<=1 && Ta::tr[real[f[t1]]]>=0)_ida=Ta::Kth(Ta::rt[Ta::tl[real[t3]]-1],Ta::rt[Ta::tr[real[t3]]],0,n+1,f_r[t1]);
				dis1++;
			}
			
			if(t2!=t3)
			{
				for(int k=20;k>=0;k--)if(d[t2]-d[t3]>(1<=1 && Ta::tr[real[f[t2]]]>=0)_idb=Ta::Kth(Ta::rt[Ta::tl[real[t3]]-1],Ta::rt[Ta::tr[real[t3]]],0,n+1,f_r[t2]);
				dis2++;
			}
		
			_Ans+=Ta::d[_ida]+Ta::d[_idb]-2*Ta::d[Ta::LCA(_ida,_idb)];
			_Ans=_Ans+dis1;_Ans=_Ans+dis2;
			out(_Ans);
			return ;
		}
		return ;
	}
};
void _read(int &x)
{
	char ch=getchar(); x=0;
	while(ch<'0' || ch>'9')ch=getchar();
	while(ch>='0' && ch<='9')
	{
		x=x*10+ch-'0'; ch=getchar();
	}
	return;
}
void _readLL(long long &x)
{
	char ch=getchar(); x=0;
	while(ch<'0' || ch>'9')ch=getchar();
	while(ch>='0' && ch<='9')
	{
		x=x*10+ch-'0'; ch=getchar();
	}
	return;
}

void work()
{
	_read(n); _read(m); _read(q);
	//scanf("%d%d%d",&n,&m,&q);
	memset(Ta::head,0,sizeof(Ta::head));
	long long x,y;
	for(int i=1;i