5.数据库索引实现原理及查询优化

1.索引：高效检索的解决方案

一般的应用系统，读写比例在10:1左右，而且一般的插入操作和更新操作很少会出现性能问题，在生产环境中出现问题的最多，也最容易出问题的还是一些复杂的查询操作，因此对于查询语句的优化显然是重中之重。说起加速查询就不得不提到索引。

索引在MySql中也叫做“键”，是存储引擎用于快速查找记录的数据结构。索引对于良好的性能非常关键，尤其当数据表中数据量越来越大的时候，索引对于性能的影响愈发重要。索引的优化应该是对查询性能优化的最重要手段了，索引能够轻易的将查询性能提升几个数量级。索引就相当于是字典里面的音序表，如果要查询某个字，不适用音序表的话我们需要从几百页里面去查找，这种速度可见有多慢。

2.索引的实现原理

索引的目的在于提高查询效率，与我们查字典的用的音序表是一个道理，先定位音节所在的页，然后再定位具体的字。这种查询方式本质上都是：通过不断的缩小想要获取数据的范围最终筛选出想要的结果，同时把随机事件变成顺序事件。也就是说有了这种索引机制，我们就可以总是用同样的查找方式来锁定数据。

数据库也是一样，但显然要复杂的多，因为不仅面临着等值查询，还有范围查询(>、<、between、in)、模糊查询(like)、并集查询(or)等等。数据库应该选择怎么样的方式来应对所有的问题呢？我们回想字典的例子，能不能把数据分成段，然后分段查询呢？最简单的如果1000条数据，1到100分成第一段，101到200分成第二段，201到300分成第三段…这样查第250条数据，只要找第三段就可以了，一下子去除了90%的无效数据。但如果是1千万的记录呢，分成几段比较好？稍有算法基础的同学会想到搜索树，其平均复杂度是lgN，具有不错的查询性能。但这里我们忽略了一个关键的问题，复杂度模型是基于每次相同的操作成本来考虑的。而数据库实现比较复杂，一方面数据是保存在磁盘上的，另外一方面为了提高性能，每次又可以把部分数据读入内存来计算，因为我们知道访问磁盘的成本大概是访问内存的十万倍左右，所以简单的搜索树难以满足复杂的应用场景。

1.索引数据的读取：磁盘IO与预读

考虑到磁盘IO是非常高昂的操作，计算机操作系统做了一些优化，当一次IO时，不光把当前磁盘地址的数据，而是把相邻的数据也都读取到内存缓冲区内，因为局部预读性原理告诉我们，当计算机访问一个地址的数据的时候，与其相邻的数据也会很快被访问到。每一次IO读取的数据我们称之为一页(page)。具体一页有多大数据跟操作系统有关，一般为4k或8k，也就是我们读取一页内的数据时候，实际上才发生了一次IO，这个理论对于索引的数据结构设计非常有帮助，而对于B+树来说因为我们默认使用自增主键来作为聚簇索引，所以它本身就是有序的，那么数据读取的时候，磁盘预读的内容就会有效，如果磁盘预读的内容使我们不需要的内容，比如说读取多个分散的小文件，那么磁盘预读的内容其实都浪费掉了，因此能不能利用磁盘预读的内容会对索引查找有很大影响。

任何一种数据结构都不是凭空产生的，一定会有它的背景和使用场景，我们现在总结一下，我们需要这种数据结构能够做些什么，其实很简单，那就是：每次查找数据时把磁盘IO次数控制在一个很小的数量级，最好是常数数量级。那么我们就想到如果一个高度可控的多路搜索树是否能满足需求呢？就这样，b+树应运而生。

2.索引的存储结构：B+Tree

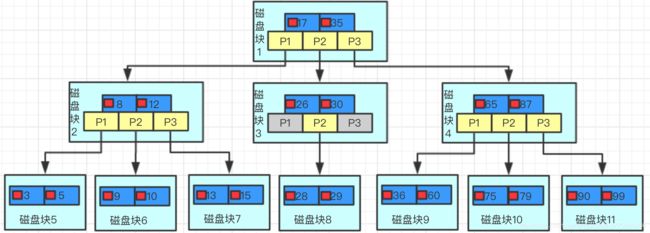
如上图，是一颗b+树，关于b+树的定义可以自己百度，这里只说一些重点，浅蓝色的块我们称之为一个磁盘块，可以看到每个磁盘块包含几个数据项（深蓝色所示）和指针（黄色所示），如磁盘块1包含数据项17和35，包含指针P1、P2、P3，P1表示小于17的磁盘块，P2表示在17和35之间的磁盘块，P3表示大于35的磁盘块。真实的数据存在于叶子节点即3、5、9、10、13、15、28、29、36、60、75、79、90、99。非叶子节点不存储真实的数据，只存储指引搜索方向的数据项，如17、35并不真实存在于数据表中。

3.b+树的查找过程

如图所示，如果要查找数据项29，那么首先会把磁盘块1由磁盘加载到内存，此时发生一次IO，在内存中用二分查找确定29在17和35之间，锁定磁盘块1的P2指针，内存时间因为非常短（相比磁盘的IO）可以忽略不计，通过磁盘块1的P2指针的磁盘地址把磁盘块3由磁盘加载到内存，发生第二次IO，29在26和30之间，锁定磁盘块3的P2指针，通过指针加载磁盘块8到内存，发生第三次IO，同时内存中做二分查找找到29，结束查询，总计三次IO。真实的情况是，3层的b+树可以表示上百万的数据，如果上百万的数据查找只需要三次IO，性能提高将是巨大的，如果没有索引，每个数据项都要发生一次IO，那么总共需要百万次的IO，显然成本非常非常高。

4.b+树性质

1.索引字段要尽量的小：

通过上面的分析，我们知道IO次数取决于b+数的高度h，假设当前数据表的数据为N，每个磁盘块的数据项的数量是m，则有h=㏒(m+1)N，当数据量N一定的情况下，m越大，h越小；而m = 磁盘块的大小 / 数据项的大小，磁盘块的大小也就是一个数据页的大小，是固定的，如果数据项占的空间越小，数据项的数量越多，树的高度越低。这就是为什么每个数据项，即索引字段要尽量的小，比如int占4字节，要比bigint8字节少一半。这也是为什么b+树要求把真实的数据放到叶子节点而不是内层节点，一旦放到内层节点，磁盘块的数据项会大幅度下降，导致树增高。当数据项等于1时将会退化成线性表。

2.索引的最左匹配特性（即从左往右匹配）：

当b+树的数据项是复合的数据结构，比如(name,age,sex)的时候，b+数是按照从左到右的顺序来建立搜索树的，创建的索引包括(name), (name,age), (name, age, sex)三个索引。比如当(张三,20,F)这样的数据来检索的时候，b+树会优先比较name来确定下一步的所搜方向，如果name相同再依次比较age和sex，最后得到检索的数据；但当(20,F)这样的没有name的数据来的时候，b+树就不知道下一步该查哪个节点，因为建立搜索树的时候name就是第一个比较因子，必须要先根据name来搜索才能知道下一步去哪里查询。比如当(张三,F)这样的数据来检索时，b+树可以用name来指定搜索方向，但下一个字段age的缺失，所以只能把名字等于张三的数据都找到，然后再匹配性别是F的数据了， 这个是非常重要的性质，即索引的最左匹配特性。

3.索引的分类

1.索引的分类

索引根据它们的用途不同可以分为以下几种类型：

• 1.普通索引index :加速查找
• 2.唯一索引
  • 主键索引：primary key ：加速查找+约束（不为空且唯一）
  • 唯一索引：unique：加速查找+约束 （唯一）
• 3.联合索引
  • -primary key(id,name):联合主键索引
  • -unique(id,name):联合唯一索引
  • -index(id,name):联合普通索引
• 4.全文索引fulltext :用于搜索很长一篇文章的时候，效果最好。
• 5.空间索引spatial :了解就好，几乎不用

组合索引的优点

组合索引占用的空间更小，过滤效率更高。组合索引的底层实现是对多个列进行排序，正常单列索引是对单列进行排序的，但是多列索引是对多列进行排序的。

2.索引的方法：hash与BTree

我们可以在创建上述索引的时候，可以为其指定索引方法：

• hash类型的索引：查询单条快，范围查询慢
• btree类型的索引：b+树，层数越多，数据量指数级增长（我们就用它，因为innodb默认支持它）

3.不同存储引擎对索引方法的支持

不同的存储引擎支持的索引类型也不一样：

• InnoDB ：支持 B-tree、Full-text 等索引，不支持 Hash 索引；
• MyISAM ：支持 B-tree、Full-text 等索引，不支持 Hash 索引；
• Memory ：支持 B-tree、Hash 等索引，不支持 Full-text 索引；

4.索引的创建

1.建表同时创建索引

CREATE TABLE 表名 (
   字段名1  数据类型 [完整性约束条件…],
    字段名2  数据类型 [完整性约束条件…],
    [UNIQUE | FULLTEXT | SPATIAL ]   INDEX | KEY
    [索引名]  (字段名[(长度)]  [ASC |DESC]) 
 );

2.在已存在的表上创建索引

 CREATE  [UNIQUE | FULLTEXT | SPATIAL ]  INDEX  索引名 
   ON 表名 (字段名[(长度)]  [ASC |DESC]) ;

3.修改存在的索引

ALTER TABLE 表名 ADD  [UNIQUE | FULLTEXT | SPATIAL ] INDEX  索引名 (字段名[(长度)]  [ASC |DESC]) ;

4.删除索引

DROP INDEX 索引名 ON 表名字;

5.索引高度计算

在InnoDB里，每个页默认16KB，假设索引的是8B的long型数据，每个key后有个页号4B，还有6B的其他数据（参考《MySQL技术内幕：InnoDB存储引擎》P193的页面数据），那么每个页的扇出系数为16KB/(8B+4B+6B)≈1000，即每个页可以索引1000个key。假设每条数据大小是100B，那么叶子节点上，一页可以存储的数据为16k/100B≈160条，那么再在高度h=3时，s=1000^2 * 160≈1.6亿！也就是说，InnoDB通过三次索引页的I/O，即可搜索1亿的数据。通常来说，索引树的高度在2~4。当然，这也跟要索引字段的数据类型有关，如果是int或short，索引效率更好，而如果是varchar(100)，那扇出系数就低了，索引效率自然要低些。所以我们在索引字段时，字段的类型越简单效率越好。

如果要计算一个B+树的高度，那么需要首先知道这个树的索引键的大小，以及每条数据的大小，这样我们大致可以评估出来索引页存放的索引数量，以及数据页里面可以存放的数据数量。

下面对通常情况下数据做一个简单的汇总：

序号	key长度	row长度	索引高度	数据量
1	8	100	3	索引页容量=16*1024/(8+4+6) = 1000 数据页容量=16*1024/100 = 160 数据量=1000 * 1000 * 160=1.6亿
2	8	200	3	索引页容量=16*1024/(8+4+6) = 1000 数据页容量=16*1024/200 = 80 数据量=1000 * 1000 * 80=8kw
3	8	500	3	索引页容量=16*1024/(8+4+6) = 1000 数据页容量=16*1024/500 = 32 数据量=1000 * 1000 * 32=3200w
4	8	1000		索引页容量=16*1024/(8+4+6) = 1000 数据页容量=16*1024/1000 = 16 数据量=1000 * 1000 * 16=1600w
5	4	100	3	索引页容量=16*1024/(4+4+6) = 1170 数据页容量=16*1024/100 = 160 数据量1170 * 1170 * 160=2.1亿
6	4	1000	3	索引页容量=16*1024/(4+4+6) = 1170 数据页容量=16*1024/100 = 16 数据量1170 * 1170 * 160=2100w

从上面可以看到，对于索引列的大小对数据量的影响是指数级的，而每一行数据量的大小对数据量的影响是数量级的。所以一般来说数据量在亿级别的一般索引高度在3左右（行数据量小，索引小），如果行数据量大，并且索引字段大的话，一般在索引高度在5左右。

5.索引使用遵循的原则

1.最左前缀匹配原则

create index ix_name_email on s1(name,email,)
select * from s1 where name='egon'; #可以
select * from s1 where name='egon' and email='asdf'; #可以
select * from s1 where email='[email protected]'; #不可以

2.=和in可以乱序

比如a = 1 and b = 2 and c = 3 建立(a,b,c)索引可以任意顺序，mysql的查询优化器会帮你优化成索引可以识别的形式。

3.选择区分度高的列作为索引

区分度的公式是count(distinct col)/count(*)，区分度表示字段不重复的比例，比例越大我们扫描的记录数越少，唯一键的区分度是1，而一些状态、性别字段可能在大数据面前区分度就是0，那可能有人会问，这个比例有什么经验值吗？使用场景不同，这个值也很难确定，一般需要join的字段我们都要求是0.1以上，即平均1条扫描10条记录。

4.索引列不能参与计算

保持列“干净”，比如from_unixtime(create_time) = ’2014-05-29’
就不能使用到索引，原因很简单，b+树中存的都是数据表中的字段值，
但进行检索时，需要把所有元素都应用函数才能比较，显然成本太大。
所以语句应该写成create_time = unix_timestamp(’2014-05-29’);

5.选择 where,on,group by,order by 中出现的列

6.选择较小的数据列

这样的索引文件更小，同时可装载更多的索引键

7.为较长的字符串使用前缀索引

举个例子：现在有个user表，列 family_name varchar(50) 保存的是英文姓氏（我也想用中文姓名来举例，但是不大适合，看下去就明白了。。。）
要取得设置前缀索引最理想的”prefix_length”，我们首先要取得整列的选择性，如下：

SELECT COUNT(DISTINCT family_name)/COUNT(*) FROM user;

假设这里得到值是0.188。

然后我们继续去看看该列前1个字符的选择性又是多少

SELECT COUNT(DISTINCT LEFT(family_name,1))/COUNT(*) FROM user;

假设这里得到的结果是0.532，和整列的选择性出入太大，不可取，继续：

SELECT COUNT(DISTINCT LEFT(family_name,2))/COUNT(*) FROM user;

SELECT COUNT(DISTINCT LEFT(family_name,3))/COUNT(*) FROM user;

…

假设直接到“prefix_length”为5时，得到的值为0.189，非常接近！

而取6时得到的值为0.18891，这个选择性和5并没有太大的偏差。

再结合减少索引文件大小的这个思路

“prefix_length”值设置为5才是此处设置前缀索引的最优方案！

8.创建组合索引

组合索引能减低索引文件的大小，使用速度也优于多个单列索引

9.切勿滥用索引

因为除了磁盘空间的开销外，每次增删改都需要重新建立索引

10.组合索引不会包含有NULL值的列

若组合索引包含NULL值的列则整个组合索引无效

6.索引失效的情况总结

1.like ‘%xx’

分析一下就能发现，索引是从左向右匹配的，左边的第一个字符是%的话，索引就不知道它改匹配什么了，因此就会失效。

2.使用函数

 select * from tb1 where reverse(email) = 'wupeiqi';

3. 组合索引最左前缀

 如果组合索引为：(name,email)
    name and email       -- 使用索引
    name                 -- 使用索引
    email                -- 不使用索引

4.隐式转换：（类型不一致）使用数字匹配varchar字段

这种情况很隐蔽，我们通过这样的查询语句是可以查询到结果的，但是索引却失效了，因为这个执行过程中mysql需要对每一列的值进行转换，把varchar转换为数字之后再进行比较，索引自然就失效了。

select * from tb1 where email = 999;

5.普通索引”!=“不走索引

对普通索引进行”!=“查询操作索引会失效，如果判断的对象是主键索引依然生效，不过即便是主键索引也不建议这么查，因为这意味着对索引进行范围查询，效率也很低。

6.排序条件和查询列必须一致

如果排序条件和查询字段必须同时为索引则select字段必须也是索引字段，否则无法命中

select name from s1 order by email desc;

7.or 中有未建立索引的列

如果name列没有建立索引将会导致索引失效

select * from tb1 where nid = 1 or name = '[email protected]';

关于Hash索引和BTree索引的性能比较

对于查询单条数据来说Hash索引效率明显要高于BTree索引，但是对于使用主键来进行范围查询的情况来说BTree的查询效率可能要高于Hash索引，因为BTree的主键索引和数据存放位置是在一起的而且是顺序存放的，而Hash索引和数据的存放是分散的，分散意味着在定位到数据之后还需要分别去取数据然后合并返回。因为存放位置不连续就需要进行多次IO操作，前面我们已经知道IO操作速度很慢，IO操作的次数越多效率越低，而对于BTree索引来说因为数据存储都是按顺序来的，所以一次IO就可以取出很多数据，显然IO的操作次数就会减少，因此BTree的范围查询不一定比Hash索引慢。