数据结构和算法学习之路——树和二叉树的详解（C++版）

树据结构之树和二叉树的详解——C++语言

“Perfection is achieved not when you have nothing more to add, but when you have nothing left to take away.” - Antoine de Saint-Exupery —— Antoine de Saint-Exupery
无一分可增不叫完美, 无一分可减才是.

(一) 关于树

1.1 树的基本概念

首先，树是一种重要的非线性数据结构，下面我们看看树大概的一些知识点

(二)关于二叉树

关于二叉树的讨论，我们在本文中以排序二叉树为例

2.1 排序二叉树

2.1.1 排序二叉树的概念

二叉排序树（Binary Sort Tree），又称二叉查找树（Binary Search Tree），也称二叉搜索树。
二叉排序树或者是一棵空树，或者是具有下列性质的二叉树：

1. 若左子树不空，则左子树上所有结点的值均小于它的根结点的值；
2. 若右子树不空，则右子树上所有结点的值均大于或等于它的根结点的值；
3. 左、右子树也分别为二叉排序树；

其实左结点的值大还是右结点的值大是自己规定的，不过为了方便统一，我们也规定右结点大于左结点

2.1.2 排序二叉树的结构

每一个二叉树的结点都会有一个左指针和右指针

struct BT
{
    int val;  //回顾树结点的概念，一个结点包括数据域和指向其子树的分支
    BT *left;  //左指针
    BT *right; //右指针
};

struct Tree
{
    BT *root;
};

2.2 二叉树的基本操作

2.2.1 排序二叉树的创建

排序二叉树不是一次性生成的，是一个结点一个结点插进去的，每一次的插入都会进行一个值的比较，来决定到底是插入在右边还是左边
先来看一下下图排序二叉树的创建过程

下面是代码的实现：

void insert(Tree* tree, int val)
{
    BT *temp, *newnode;
    newnode = new BT;    //newnode用来开辟一个新的结点来存放要插入的数据
    newnode->val = val;
    newnode->right = NULL;
    newnode->left = NULL;
    
    if(tree->root == NULL)
    {
        tree->root = newnode;
    }
    else
    {
        temp = tree->root;      //temp从根节点开始判断要插入的位置
        while(NULL != temp)
        {
            if(temp->val < newnode->val)   //说明应该往右边插入
            {
                if(temp->right == NULL)
                {
                    temp->right = newnode;
                    return;      //注意，这里成功插入之后一定要return掉，否则程序会继续进行就会导致中断
                }
                else
                {
                    temp = temp->right;
                }
            }
            else
            {
                if(temp->left == NULL)
                {
                    temp->left = newnode;
                    return;
                }
                else
                {
                    temp = temp->left;
                }
            }
        }
    }
}

2.2.2 排序二叉树的遍历

1.先序遍历

记忆方法：根左右，即先访问根节点，再访问左结点，最后访问右结点
就以上面我们构造好的排序二叉树为例，其实每一个结点都可以看成是其下方子树的根节点，那么我们发现，当第一次根左右访问到56的左结点43时，43又可以看成是其下方子树的根节点，那么就开始了第二次的根左右，以此类推，虽然说这个遍历的代码看起来很简洁，但是设计出来还真是需要很强的编程功底。那么这棵排序二叉树的先序遍历结果就是:
56 43 12 34 23 43 56

具体实现的代码如下

void preorder(BT* ptr)
{
    if(ptr != NULL)
    {
        cout<<ptr->val<<" ";
        preorder(ptr->left);    //实际上是一个递归的过程
        preorder(ptr->right);
    }
}

2.中序遍历

记忆方法：左根右，具体的方法和先序遍历大同小异
上述二叉树的中序遍历的结果是：12 23 34 43 43 56 56

具体实现的代码如下

void midorder(BT *ptr)
{
    if(ptr != NULL)
    {
        midorder(ptr->left);
        cout<<ptr->val<<" ";
        midorder(ptr->right);
    }
}

3.后序遍历

记忆方法：左右根
上述排序二叉树后序遍历的结果是: 23 34 12 43 43 56 56

void postorder(BT *ptr)
{
    if(ptr != NULL)
    {
        postorder(ptr->left);
        postorder(ptr->right);
        cout<<ptr->val<<" ";
    }
}

三种遍历的一些特点

对于先序遍历，第一个元素肯定是根节点元素
对于中序遍历

1. 假定我们知道了根节点是多少，那么遍历结果中根节点以左的就是左子树的全部
   元素，根节点以右的就是右子树的全部元素
2. 对于中序遍历，假设以学生成绩的大小score创建二叉树，那么遍历的结果就是score按从小到大排列所得
3. 中序遍历的第一个结点是二叉树的最左结点

对于后序遍历，第一个结点代表最左边的结点，最后一个节点代表根节点

2.2.3 排序二叉树的删除

二叉树的删除是一个比较麻烦的过程，它分成了以下几种情况

1. 删除根节点
2. 删除非根结点，且该节点既无左子树又无右子树
3. 删除非根结点，且该节点有左子树或者右子树
4. 删除非根结点，且该节点既有左子树又有右子树

要想删除，首先必须要找到要删除的结点及其父结点，找父结点经常使用滞后法，下面我们来看看具体是怎么实现的吧

int del_num;
BT *ptr, *p_father, *temp, *cur;
cin>>del_num;
ptr = tree->root;
while(ptr != NULL)
{
    if(ptr->val < del_num)     //此时应该往右半子树去查找
    {
        if(ptr->right == NULL)
        {
            cout<<"Can't find!"<<endl;
            return;
        }
        else
        {
            p_father = ptr;
            ptr = ptr->right;
        }
    }
    //ptr->val 小于del_num的情况也是类似，这里不再赘述
}

下面看看最简单的情况2，以上图我们构造好的二叉树为例，假设要删除23，我们先找到了它的父结点是34，经过判断后发现23是34的左子树，所以我们令34的左指针指向NULL，就完成了删除操作而情况2里面又分了三个小情况，1. 只有根节点 2. 删除的是父结点的右结点 3.删除的是父结点的左结点

那么再看看情况3，这个也比较简单，说白了就是子承父业嘛，孩子接替被删除的父结点未完成的大业，比如要删除的是12结点，很好，我们发现12结点仅有右子树，那么很明显就是有34其接替12，和43相连接

//只有左子树
if(ptr->left != NULL && ptr->right == NULL)
{
    if(ptr == tree->root)    //删除根节点的情况
    {
       tree->root = ptr->left;
       return;
    }
    if(p_father->left == ptr)
    {
        p_father->left = ptr->left;
        return;
    }
    if(p_father->right == ptr)
    {
        p_father->right = ptr->left;
        return;
    }
}

下面到了最后一个情况，删除非根结点，且该节点既有左子树又有右子树，这应该怎么做呢？答案是，我们应该找出要删除结点的右子树的最左结点，用这个结点去替换要删除的结点，这段我打算直接贴代码，大家用笔把删除过程自己走一遍绝对就清楚了，我当时就是这么干的

if(ptr->left != NULL && ptr->left != NULL)
{
    if(ptr == tree->root)
    {
        temp = ptr->right;
        cur = ptr;
        while(temp != NULL)
        {
            cur = temp;
            temp = temp->left;
        }
        ptr->val = temp->val;    //做值的交换
        if(cur != ptr)
        {
            cur->left = temp->right;
        }
        else
        {
            cur->right = temp->left;
        }
        return;
    }
}

剩下的情况，比如说p_father之类的情况和这个几乎一样
我们发现删除根节点的情况并不是单独列出来的，而是交织在了删除各个情况的结点里面，但是有一点特别需要注意，由于计算机的编译一般情况下是顺序执行的，由于假设删除的是根节点，根节点是没有p_father的，如果我们把删除根节点的情况放在了后边，比如说放在了p_father->left = ptr这个情况的后面，那么编译器运行的时候就会中断，所以一定要把删除根节点的情况放在第一，我当时也是遇到了这个情况，所以这里特别记录一下。

(三)关于赫夫曼树(最优二叉树)

3.1 赫夫曼树的基本概念

1. 路径长度: 从树中一个结点到另一个结点之间的分支构成这两个结点之间的路径，路径上分支的数目称为路径长度
2. 树的路径长度: 从树根到每一个结点的路径长度之和
3. 结点的带权路径长度: 从该结点到树根之间的路径长度与该结点的权重的乘积
4. 树的带权路径长度: 树中所有叶子结点的带权路径长度之和（WPL)

赫夫曼树，就是树的带路径长度最小的树，下面我们看几个例子加深对赫夫曼树的理解

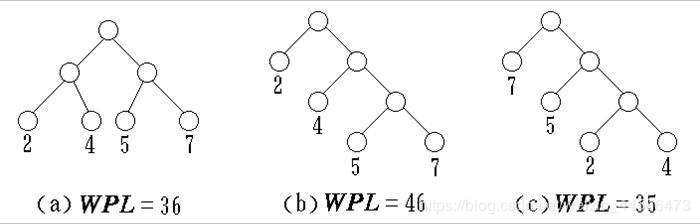
对于图(a)，它的WPL = 2x2 + 2x4 + 2x5 + 2x7 = 36
对于图(b)，它的WPL = 1x2 + 2x4 + 3x5 + 3x7 = 46
对于图©，它的WPL = 1x7 + 2x5 + 3x2 + 3x4 = 35
显然图©是一个赫夫曼树

3.2 赫夫曼树的构造思路

比如说给了你一堆带有权重的结点，要求你构造出一棵赫夫曼树
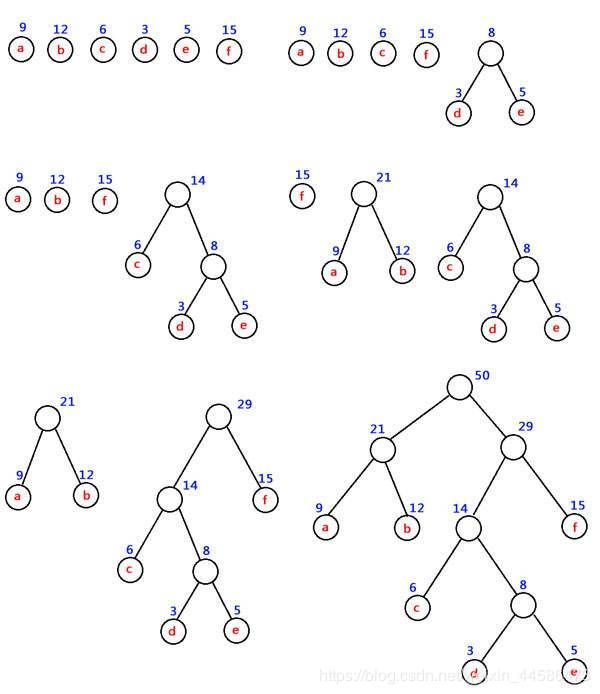
首先，你得从这一堆结点中找到权值最小的两个结点，以他们两个作为叶子结点先构建一棵子树，然后把这两个结点从原来的结点堆里面删除，把他们的父结点(其权重为原来两结点权重的加和)加入到结点堆里面继续进行比较
之和呢，就是继续在这个结点堆里面找出两个最小权值的结点，然后继续按照上述的方法构造，直到所有结点用完

下面我们来看看创建的过程图