[HNOI&AHOI2017] NOIP考挂蒟蒻的一篇游记 && 部分题解
Day0
犹记得上次NOIP329却切了Day1T2…这次似乎翻盘很困难……?
咸鱼选手试机写了个Pollard-rho 震惊地发现srand(19260817)之后随机的long long数竟然是2*大素数形式 还以为我写错了。
隔了一个座位的wyx敲了一个SA和FFT,期间稳爷爷约5-10分钟来奶wyx霸霸一次,然后开始互奶。
后来wlp和zzy来了,场面一度失控(捂脸)
(可能是因为太久没上语文了已经不会写文章了)
Day1
拿到题看了看T1的spaly,画了画图就扔了,感觉不是很可做。
看了看T2 似乎是道计数题 怕是还是可以做的 先扔了看T3去
然后看了下T3发现是傻逼题 直接敲了个NTT就过了样例 拍了拍暴力数据 感觉没啥错 就去看前面的题了(全世界都A了T3)
于是又看了看T2 没看出第一个情况只有O(n)种 感觉暴力还是很好写的 先丢一边了
研究T1的性质 发现单旋最小值就是只有最小值的右子树深度不变 其他都+1 单旋最大值也差不多 感觉还是不太可做
yy了一个splay维护整棵树的dfs序的写法 开始大力码码码 码好之后开始调调调 前后大概花了3h+ 总算是和暴力拍上了 感觉很兴奋(然而只有本傻逼选手写的是splay维护dfs序 wlp是LCT wyx直接一棵线段树就艹过去了 为什么不强制在线呜呜呜 全世界都A了T1)
然后就玩了玩T2的暴力30分 写了一个可持久化线段树的60 不想拍了(其实来不及了有点慌)就直接交了
T2 第一个情况竟然那么少?????????????
(全世界都A了T2)
出来没有fst T1和T3我是很开心的 T2的暴力30也在预想之中 似乎把NOIP考挂的差距填回来了
Day2
这个T1数据范围这么小…全场都会做?
然后我就发现自己并不会什么多项式做法 先去看T2
woc计算几何?
滚去看T3
诶我好像不会 敲个70暴力吧。。
然后滚回去看T2 还是不会 跑去写T1暴力
嗯这个T1暴力很靠谱……?于是码了一个dp贪心了一下 然后dfs暴力一下 瞎jb剪剪枝
竟然A了?
然后又敲了个T2暴力 想了想加了一句
if (n >= 100000) {puts("nan");return 0;}
居然给我续了20pts……感觉会被ban掉……
于是day2就220……?懵--
wyx霸霸还是好稳啊 怒艹稳爷爷 可怕
wlp day2怎么翻车了啊 不懂
-------------------------------------------分割线-------------------------------------------
放一下其中几道题的题解吧。。
Day1T1 单旋 spaly
题意:给一棵spaly 要求支持插入 单旋最小值 单旋最大值 单旋删除最小值 单旋删除最大值 每次输出上次操作节点深度 数据范围1E5
听说可以splay直接暴力维护这棵spaly 反正我是维护了整棵spaly的dfs序 然后我们来看每个操作
我们考虑 我们将每个点拆成了入(深度+1) 出(深度-1) 因此求一个点的深度其实就是求这个点的入/出在整个dfs序上的前缀和,可以均摊O(log n)统计答案。
我们考虑dfs序怎么维护,首先考虑操作1:加入一个节点
显然加入的这个节点要么被挂在前继的右边 要么被挂在后继的左边 而这取决于前继和后继谁的深度更小
因此我们只要查询一下哪个是父亲 如果是这个数的前继 其右子树一定为空 直接在它的出点前面插入即可
如果是这个数的后继 左子树一定为空 只要在入点后面插入
操作2:将最小值旋转到根
我们发现最小值旋转到根后 它只有右子树 并且整个森林中其他值的dfs序位置不变
所以我们将这个最小值提出来 分开放到整个dfs序列的最前面和最后面就可以了
操作3:将最大值旋转到根
和操作2相似
操作4和操作5:先做一次对应操作 再删去两个节点即可
时间复杂度O(nlogn)
#include"algorithm"
#include"iostream"
#include"stdlib.h"
#include"stdio.h"
#include"math.h"
#include"vector"
#include"queue"
#include"map"
#include"set"
using namespace std;
const int N=100005;
struct node{
node*c[2],*fa;
int flag,sum,sz;
node();
void pushup();
}Tnull,*null=&Tnull,a[2][N];
node::node(){
c[0]=c[1]=fa=null;
flag=0,sum=0,sz=0;
}
void node::pushup(){
sz=c[0]->sz+c[1]->sz+1;
sum=c[0]->sum+flag+c[1]->sum;
}
void rotate(node*x,node*&f){
node*y=x->fa,*z=y->fa;
if(y==f)f=x;else if(z!=null)z->c[z->c[1]==y]=x;
int l=y->c[1]==x,r=l^1;
if(x->c[r]!=null)x->c[r]->fa=y;
y->fa=x,x->fa=z,y->c[l]=x->c[r],x->c[r]=y,y->pushup();
}
void splay(node*x,node*&f){
while(x!=f){
node*y=x->fa,*z=y->fa;
if(y!=f){
if((z->c[0]==y)^(y->c[0]==x))rotate(x,f);
else rotate(y,f);
}
rotate(x,f);
}
x->pushup();
}
map dat;
node*rt=null;
int query_deep(int x){
node*y=&a[0][x];
splay(y,rt);
return y->c[0]->sum+y->flag;
}
void insert_back(node*x,node*i){
splay(x,rt);
i->c[1]=x->c[1];
if(x->c[1]!=null)x->c[1]->fa=i;
x->c[1]=i,i->fa=x;
i->pushup(),x->pushup();
}
void insert_front(node*x,node*i){
splay(x,rt);
i->c[0]=x->c[0];
if(x->c[0]!=null)x->c[0]->fa=i;
x->c[0]=i,i->fa=x;
i->pushup(),x->pushup();
}
int getsiz(int x){
node*l=&a[0][x],*r=&a[1][x];
splay(l,rt),splay(r,rt->c[1]);
return rt->c[1]->c[0]->sz;
}
node*findfr(node*x){
if(x->c[0]!=null)return findfr(x->c[0]);
return x;
}
node*finded(node*x){
if(x->c[1]!=null)return finded(x->c[1]);
return x;
}
void insert(int x,int key){
a[0][x].flag=1,a[0][x].pushup();
a[1][x].flag=-1,a[1][x].pushup();
if(rt==null){
rt=&a[0][x],insert_back(rt,&a[1][x]);
dat[key]=x;
printf("%d\n",query_deep(x));
return;
}
map::iterator i=dat.lower_bound(key);
if(i==dat.begin()){
int d=i->second;
insert_back(&a[0][d],&a[0][x]);
insert_back(&a[0][x],&a[1][x]);
}else if(i==dat.end()){
--i;
int d=i->second;
insert_front(&a[1][d],&a[0][x]);
insert_back(&a[0][x],&a[1][x]);
}else{
map::iterator j=i;
--i;
if(getsiz(i->second)>getsiz(j->second)){
int d=j->second;
insert_back(&a[0][d],&a[0][x]);
insert_back(&a[0][x],&a[1][x]);
}else{
int d=i->second;
insert_front(&a[1][d],&a[0][x]);
insert_back(&a[0][x],&a[1][x]);
}
}
dat[key]=x;
printf("%d\n",query_deep(x));
}
void erase(node*x){
splay(x,rt);
if(x->c[1]==null){
rt=x->c[0];
x->c[0]=null;
return;
}
node*y=findfr(x->c[1]);
splay(y,x->c[1]);
rt=x->c[1];
if(x->c[0]!=null)x->c[0]->fa=rt;
rt->c[0]=x->c[0];
x->c[1]=null,x->c[0]=null;
rt->pushup();
}
void outtree(node*x){
if(x->c[0]!=null)outtree(x->c[0]);
if(x->flag==-1)printf("%d ",x-&a[1][0]);
else printf("%d ",x-&a[0][0]);
if(x->c[1]!=null)outtree(x->c[1]);
}
void makeroot(int id){
int ans=query_deep(id);
printf("%d\n",ans);
erase(&a[0][id]);
node*x=findfr(rt);
insert_front(x,&a[0][id]);
erase(&a[1][id]);
node*y=finded(rt);
insert_back(y,&a[1][id]);
}
void splay_mn(bool del){
map::iterator i=dat.begin();
makeroot(i->second);
if(del)dat.erase(i);
}
void splay_mx(bool del){
map::iterator i=dat.end();
--i;
makeroot(i->second);
if(del)dat.erase(i);
}
void del_mn(){
splay_mn(1);
node*x=findfr(rt);
node*y=finded(rt);
erase(x),erase(y);
}
void del_mx(){
splay_mx(1);
node*x=findfr(rt);
node*y=finded(rt);
erase(x),erase(y);
}
int n,m;
int main(){
freopen("splay.in","r",stdin);
freopen("splay.out","w",stdout);
null->c[0]=null->c[1]=null->fa=null;
scanf("%d",&n);
for(int i=1,opt,key;i<=n;i++){
scanf("%d",&opt);
switch(opt){
case 1:scanf("%d",&key);insert(++m,key);break;
case 2:splay_mn(0);break;
case 3:splay_mx(0);break;
case 4:del_mn();break;
case 5:del_mx();break;
}
}
return 0;
} Day1T2 影魔 sf
题意 给定排列a 长度2E5 设L[i]为i左边第一个大于a[i]的值 R[i]为i右边第一个大于a[i]的值
2E5组l,r,求∑[l<=i
这是我的做法……可能比较繁琐 但是起码……是可以过的吧
时间复杂度O((6n+12m)logn)=O((n+m)logn)
#include"algorithm"
#include"iostream"
#include"stdlib.h"
#include"stdio.h"
#include"math.h"
#include"vector"
#include"queue"
#include"map"
#include"set"
#define last last_
using namespace std;
typedef long long LL;
const int N=200005;
int n,m,p1,p2,a[N],st[N],tp,L[N],R[N];
LL ans;
const int M=24000005;
LL sum[M];
int ls[M],rs[M],ndc;
void add(int&x,int last,int l,int r,int p,int u){
x=++ndc,sum[x]=sum[last]+u,ls[x]=ls[last],rs[x]=rs[last];
if(l==r)return;
int mid=(l+r)>>1;
if(p<=mid)add(ls[x],ls[last],l,mid,p,u);
else add(rs[x],rs[last],mid+1,r,p,u);
}
LL qry(int x,int l,int r,int s,int t){
if(sum[x]==0)return 0;
if(l==s&&r==t)return sum[x];
int mid=(l+r)>>1;
if(t<=mid)return qry(ls[x],l,mid,s,t);
if(s>mid)return qry(rs[x],mid+1,r,s,t);
return qry(ls[x],l,mid,s,mid)+qry(rs[x],mid+1,r,mid+1,t);
}
LL ask(int*rt,int l,int r,int L,int R,int S,int T){
return qry(rt[r],L,R,S,T)-qry(rt[l-1],L,R,S,T);
}
int rt[6][N];
int main(){
freopen("sf.in","r",stdin);
freopen("sf.out","w",stdout);
scanf("%d%d%d%d",&n,&m,&p1,&p2);
int w1=p1-2*p2,w2=p2;
for(int i=1;i<=n;i++)scanf("%d",&a[i]);
for(int i=1;i<=n;i++){
while(tp&&a[st[tp]]=1;i--){
while(tp&&a[st[tp]]i);
}
for(int i=1,l,r;i<=m;i++,ans=0){
scanf("%d%d",&l,&r);
ans+=(ask(rt[1],l,r,0,d,0,r-1)+ask(rt[0],l,r,0,d,r,d)*r)*w2;
ans-=(ask(rt[3],l,r,0,d,l+1,d)+ask(rt[2],l,r,0,d,0,l)*l)*w2;
ans+=(ask(rt[4],l,r,0,d,0,r)+ask(rt[5],l,r,0,d,l,d))*w1;
printf("%lld\n",ans);
}
return 0;
} Day1T3 礼物 gift
题意 给两个序列x和y 长度5E4 数字范围1-100 求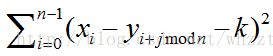 的最小值
的最小值
然后就做完了 k可以暴力枚举 发现旋转次数和k独立 因为这个值很小 所以用NTT求一下那个和旋转次数有关的值的最大值即可
时间复杂度O(nlogn+m)
#include"algorithm"
#include"iostream"
#include"stdlib.h"
#include"stdio.h"
#include"math.h"
#include"vector"
#include"queue"
#include"map"
#include"set"
using namespace std;
typedef long long LL;
const int N=50005,M=266666;
const int P=998244353,g=3;
int power(int a,int t,int P){
int r=1;
while(t){
if(t&1)r=(LL)r*a%P;
a=(LL)a*a%P;t>>=1;
}
return r;
}
int wn_[25];
void pre(){for(int i=0;i<22;i++)wn_[i]=power(g,(P-1)>>i,P);}
void transform(int A[],int len,int dft){
int i,j=len>>1,k,l,c=0;
for(i=1;i>1;j>=k;j-=k,k>>=1);
j+=k;
}
for(l=2;l<=len;l<<=1){
i=l>>1;
int wn=wn_[++c];
for(j=0;j Day2T1 大佬 dalao
题意略
我们发现怼dalao的次数和dalao的血量无关 所以我们可以先做一个dp 得到怼dalao的最多天数
然后我们就可以大力搜搜搜了
我们发现这个怼dalao的天数也很少 所以可以暴力枚举
首先考虑假如一次要怼一个dalao k点自信 的最少步数
我们可以枚举最高到达的等级 这个等级一定大于等于k的最大质因子 一定是k的约数 又不会超过步数上限
所以这里可以剪很多 check一次虽然还是O(n^2) 但是会快很多
然后我们就可以暴力处理怼dalao一次的情况
对于怼两次的情况 我们暴力步数较少的那一边 就是我们搜索这个怼掉的自信值k 然后大力剪剪枝就可以过了
我也不知道时间复杂度是什么。
#include"algorithm"
#include"iostream"
#include"stdlib.h"
#include"string.h"
#include"stdio.h"
#include"math.h"
#include"vector"
#include"queue"
#include"map"
#include"set"
using namespace std;
const int jp[]={2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97};
const int N=105,INF=(int)1e9;
int n,m,mc,a[N],w[N],C[N],dp[N][N],k,fl[N],maxc,tmp;
map s;
int dat[1000005];
int find(int x){
if(x<=1000000)return dat[x];
return s[x];
}
void insert(int x,int ans){
if(x<=1000000)dat[x]=ans;
else s[x]=ans;
}
int calc(int n){
if(n<0)return INF;
if(n==0)return 0;
if(n==1)return 1;
int l=n,ed=1;
for(int i=0;i<25;i++)while(l%jp[i]==0)ed=jp[i],l/=jp[i];
if(l>1)return INF;
if(find(n))return find(n);
int lim=k+1;
for(int i=ed;i=2&&t<=lim&&l>1;j--)while(l%j==0){l/=j;++t;}
if(l==1)lim=min(lim,t);
}
insert(n,lim);
return lim;
}
void dfs(int x,int pos){
if(tmp==m)return;
int t=calc(x);
if(t>k/2)return;
for(int i=pos;i>=0;i--)if((long long)x*jp[i]<=maxc)dfs(x*jp[i],i);
for(int i=0;i<=k-2*t;i++){
for(int j=1;j<=m;j++)if(!fl[j]){
int l=calc(C[j]-x-i);
if(l+t+i<=k)fl[j]=1,++tmp;
}
}
}
int main(){
freopen("dalao.in","r",stdin);
freopen("dalao.out","w",stdout);
scanf("%d%d%d",&n,&m,&mc);
for(int i=1;i<=n;i++)scanf("%d",&a[i]);
for(int i=1;i<=n;i++)scanf("%d",&w[i]);
for(int i=1;i<=m;i++)scanf("%d",&C[i]),maxc=max(maxc,C[i]);
memset(dp,-1,sizeof(dp));
dp[0][0]=mc;
for(int i=0;i Day2T2 队长快跑 captain
计算几何题 不会 会了再填坑
Day2T3 抛硬币 coin
题意:问n次抛硬币正面的数量比m次抛硬币正面的数量多的方案数mod 10^k的值 n,m是1E18级别 k<=9 n>=m n-m<=10000
这个题好棒啊。。反正我是智商不太够。。
首先我们考虑在n个里面选i个 在m个中选j个的方案数
就变成了 ∑[i>j]C(n,i)*C(m,j)
真是遗憾 反正我是不会继续推式子了
但是我们可以将问题进行一次转化
i>j可以转化为i-j>0
你可能会问这有什么重要的意义吗 但是我们再将这个式子变一下 就变成了
i+m-j>m
问题就转化为在n+m个物品里面选择超过m个物品的方案数 显然我们把这些物品排好 每个左边的n个和右边的m个与上面的方案是一一对应的
所以式子就变成了∑[i=m+1...n+m] C(n+m,i)
但是还是有一个问题 这个组合数如何计算
我们很想暴力使用扩展Lucas定理 但是这样就变成了O(Tk(n-m)logn)会TLE
可能会有一些卡常的技巧 但是这里完全可以求出第一个组合数 mod 2^k 用 2^p*c 表示的结果 和 mod 5^k 用 5^p * c表示的结果
而我们做CRT时的exgcd值是固定的 可以一直使用
这样的时间复杂度就是O(Tk(n-m+logn))的
其实这里可以将k去掉 只要预处理出2和5的9次以下幂就可以了 但是似乎并没有什么必要
#include"bits/stdc++.h"
using namespace std;
typedef long long LL;
const int Mod=1000000000;
const int Mod1=1<<9,Mod2=Mod>>9;
const int ex1=1537323,ex2=-403;
void exgcd(int a,int b,int&x,int&y){
if(b==0){x=1,y=0;return;}
exgcd(b,a%b,y,x);y-=a/b*x;
}
int inv(int a,int mod){
int x,y;exgcd(a,mod,x,y);
return (x%mod+mod)%mod;
}
int CRT(int r2,int r5){return ((((LL)(r5-r2)*ex1%Mod<<9)+r2)%Mod+Mod)%Mod;}
int power(int a,LL t,int P){
int r=1;
while(t){
if(t&1)r=(LL)r*a%P;
a=(LL)a*a%P;t>>=1;
}
return r;
}
LL n,m;
int k;
char ot[23];
void output(int n){
for(int i=1;i<=k;i++)ot[i]=n%10+'0',n/=10;
for(int i=k;i>=1;i--)putchar(ot[i]);
putchar('\n');
}
const int N=2000005;
int fac[2][N];
LL gd(LL n,int d){
if(n![[HNOI&AHOI2017] NOIP考挂蒟蒻的一篇游记 && 部分题解_第1张图片](http://img.e-com-net.com/image/info8/48186f6068504771b603bac78a203598.png)
![[HNOI&AHOI2017] NOIP考挂蒟蒻的一篇游记 && 部分题解_第2张图片](http://img.e-com-net.com/image/info8/50f0ee77460f407380a7d80fbe9b81c7.png)
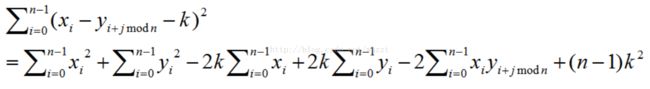
![[HNOI&AHOI2017] NOIP考挂蒟蒻的一篇游记 && 部分题解_第3张图片](http://img.e-com-net.com/image/info8/26f090de946b48bb99329eb43454c2dd.jpg)