第十五章 Caché 算法与数据结构 堆排序
文章目录
-
第十五章 Caché 算法与数据结构 堆排序 - 二叉堆特性
- 调整
- 步骤
- 完整代码
- 堆排序类
- 调用
- 降序
- 升序
- 复杂度
- 堆排序与快速排序区别
第十五章 Caché 算法与数据结构 堆排序
二叉堆特性
-
最大堆的堆顶是整个堆中的最大元素。
-
最小堆的堆顶是整个堆中的最小元素。
调整
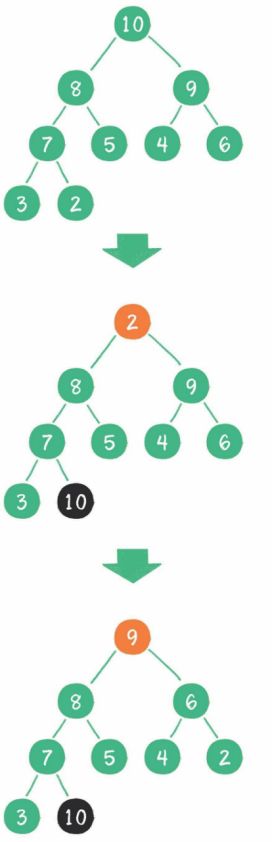
以最大堆为例,如果删除一个最大堆的堆顶(并不是完全删除,而是跟末尾的节点交换位置),经过自我调整,第2大的元素就会被交换上来,成为最大堆的新堆顶。
- 如上图所示,在删除值为10的堆顶节点后,经过调整,值为9的新节点就会顶 替上来;在删除值为9的堆顶节点后,经过调整,值为8的新节点就会顶替上来。
- 由于二叉堆的这个特性,每一次删除旧堆顶,调整后的新堆顶都是大小仅次于旧堆顶的节点。那么只要反复删除堆顶,反复调整二叉堆,所得到的集合就会成为一个有序集合。
步骤
- 把无序数组构建成二叉堆。需要从小到大排序,则构建成最大堆;需要从大到小排序,则构建成最小堆。
- 循环删除堆顶元素,替换到二叉堆的末尾,调整堆产生新的堆顶。
完整代码
堆排序类
Class PHA.YX.Arithmetic.HeapSort Extends %RegisteredObject
{
/// 下沉调整
Method downAjustArrayDesc(array As %ArrayOfDataTypes, parentIndex As %Integer, length As %Integer)
{
#dim temp as %Integer = array.GetAt(parentIndex)
#dim childIndex as %Integer = 2 * parentIndex + 1
while(childIndex < length){
;w "childIndex i:"_childIndex _ " array.GetAt(childIndex + 1):" _array.GetAt(childIndex + 1)_ " array.GetAt(childIndex):" _array.GetAt(childIndex),!
/* 如果有右孩子,且右孩子小于左孩子的值,则定位到右孩子 */
if (((childIndex + 1) < length)&&(array.GetAt(childIndex + 1) < array.GetAt(childIndex))){
s childIndex = childIndex + 1
}
;b:temp=1
;w "temp:"_temp _ " array.GetAt(childIndex):"_array.GetAt(childIndex),!
;w "childIndex:"_childIndex,!
;w array.GetAt(childIndex),!
/* 如果父节点小于任何一个孩子的值,直接跳出 */
if (temp <= array.GetAt(childIndex)){
quit /* 这一定是quit 而不是continue */
}
/* 无需真正交换,单向赋值即可 */
d array.SetAt(array.GetAt(childIndex), parentIndex)
s parentIndex = childIndex
s childIndex = 2 * childIndex + 1
}
d array.SetAt(temp, parentIndex)
}
/// 下沉调整
Method downAjustArrayAsc(array As %ArrayOfDataTypes, parentIndex As %Integer, length As %Integer)
{
#dim temp as %Integer = array.GetAt(parentIndex)
#dim childIndex as %Integer = 2 * parentIndex + 1
while(childIndex < length){
;w "childIndex i:"_childIndex _ " array.GetAt(childIndex + 1):" _array.GetAt(childIndex + 1)_ " array.GetAt(childIndex):" _array.GetAt(childIndex),!
/* 如果有右孩子,且右孩子小于左孩子的值,则定位到右孩子 */
if (((childIndex + 1) < length)&&(array.GetAt(childIndex + 1) > array.GetAt(childIndex))){
s childIndex = childIndex + 1
}
;b:temp=1
;w "temp:"_temp _ " array.GetAt(childIndex):"_array.GetAt(childIndex),!
;w "childIndex:"_childIndex,!
;w array.GetAt(childIndex),!
/* 如果父节点小于任何一个孩子的值,直接跳出 */
if (temp >= array.GetAt(childIndex)){
quit /* 这一定是quit 而不是continue */
}
/* 无需真正交换,单向赋值即可 */
d array.SetAt(array.GetAt(childIndex), parentIndex)
s parentIndex = childIndex
s childIndex = 2 * childIndex + 1
}
d array.SetAt(temp, parentIndex)
}
Method heapSortDesc(array As %ArrayOfDataTypes)
{
/* 从最后一个非叶子节点开始,依次下沉调整 */
f i = (array.Count() - 2) \ 2 : -1 : 0 d
.;w "i:"_ i,!
.d ..downAjustArrayDesc(array, i, array.Count())
zw array
f i = (array.Count() - 1) : -1 : 1 d
.s temp = array.GetAt(i)
.d array.SetAt(array.GetAt(0), i)
.d array.SetAt(temp, 0)
.d ..downAjustArrayDesc(array, 0, i)
q array
}
Method heapSortAsc(array As %ArrayOfDataTypes)
{
/* 从最后一个非叶子节点开始,依次下沉调整 */
f i = (array.Count() - 2) \ 2 : -1 : 0 d
.;w "i:"_ i,!
.d ..downAjustArrayAsc(array, i, array.Count())
zw array
f i = (array.Count() - 1) : -1 : 1 d
.s temp = array.GetAt(i)
.d array.SetAt(array.GetAt(0), i)
.d array.SetAt(temp, 0)
.d ..downAjustArrayAsc(array, 0, i)
q array
}
}
调用
降序
Method heapSortDesc(array As %ArrayOfDataTypes)
{
/* 从最后一个非叶子节点开始,依次下沉调整 */
f i = (array.Count() - 2) \ 2 : -1 : 0 d
.;w "i:"_ i,!
.d ..downAjustArrayDesc(array, i, array.Count())
zw array
f i = (array.Count() - 1) : -1 : 1 d
.s temp = array.GetAt(i)
.d array.SetAt(array.GetAt(0), i)
.d array.SetAt(temp, 0)
.d ..downAjustArrayDesc(array, 0, i)
q array
}
DHC-APP>w ##class(PHA.YX.Arithmetic).HeapSortDesc()
array=<OBJECT REFERENCE>[1@%Library.ArrayOfDataTypes]
+----------------- general information ---------------
| oref value: 1
| class name: %Library.ArrayOfDataTypes
| reference count: 3
+----------------- attribute values ------------------
| Data(0) = 0
| Data(1) = 1
| Data(2) = 2
| Data(3) = 6
| Data(4) = 3
| Data(5) = 7
| Data(6) = 8
| Data(7) = 9
| Data(8) = 10
| Data(9) = 5
| ElementType = "%String"
+-----------------------------------------------------
array=<OBJECT REFERENCE>[1@%Library.ArrayOfDataTypes]
+----------------- general information ---------------
| oref value: 1
| class name: %Library.ArrayOfDataTypes
| reference count: 2
+----------------- attribute values ------------------
| Data(0) = 10
| Data(1) = 9
| Data(2) = 8
| Data(3) = 7
| Data(4) = 6
| Data(5) = 5
| Data(6) = 3
| Data(7) = 2
| Data(8) = 1
| Data(9) = 0
| ElementType = "%String"
+-----------------------------------------------------
升序
Method heapSortAsc(array As %ArrayOfDataTypes)
{
/* 从最后一个非叶子节点开始,依次下沉调整 */
f i = (array.Count() - 2) \ 2 : -1 : 0 d
.;w "i:"_ i,!
.d ..downAjustArrayAsc(array, i, array.Count())
zw array
f i = (array.Count() - 1) : -1 : 1 d
.s temp = array.GetAt(i)
.d array.SetAt(array.GetAt(0), i)
.d array.SetAt(temp, 0)
.d ..downAjustArrayAsc(array, 0, i)
q array
}
DHC-APP>w ##class(PHA.YX.Arithmetic).HeapSortAsc()
array=<OBJECT REFERENCE>[1@%Library.ArrayOfDataTypes]
+----------------- general information ---------------
| oref value: 1
| class name: %Library.ArrayOfDataTypes
| reference count: 3
+----------------- attribute values ------------------
| Data(0) = 10
| Data(1) = 9
| Data(2) = 8
| Data(3) = 6
| Data(4) = 5
| Data(5) = 7
| Data(6) = 2
| Data(7) = 3
| Data(8) = 1
| Data(9) = 0
| ElementType = "%String"
+-----------------------------------------------------
array=<OBJECT REFERENCE>[1@%Library.ArrayOfDataTypes]
+----------------- general information ---------------
| oref value: 1
| class name: %Library.ArrayOfDataTypes
| reference count: 2
+----------------- attribute values ------------------
| Data(0) = 0
| Data(1) = 1
| Data(2) = 2
| Data(3) = 3
| Data(4) = 5
| Data(5) = 6
| Data(6) = 7
| Data(7) = 8
| Data(8) = 9
| Data(9) = 10
| ElementType = "%String"
+-----------------------------------------------------
复杂度
- 把无序数组构建成二叉堆,这一步的时间复杂度是O(n)。
- 需要进行n-1次循环。每次循环调用一次downAdjust方法,所以第2步的计算规模是 (n-1)×logn ,时间复杂度为O(nlogn)。
- 两个步骤是并列关系,所以整体的时间复杂度是O(nlogn)。
堆排序与快速排序区别
- 快速排序的最坏时间复杂度是O(n2),而堆排序的最坏时间复杂度稳定在O(nlogn)。
- 快速排序递归和非递归方法的平均空间复杂度都是O(logn),而堆排序的空间复杂度是O(1)。