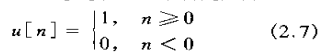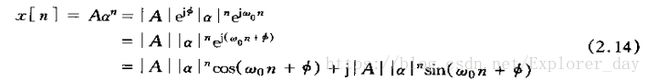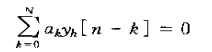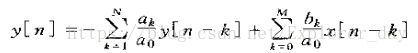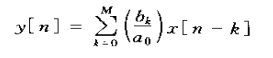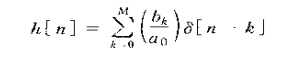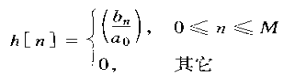《离散时间信号处理学习笔记》—离散时间信号与系统（一）

注：本博客是基于奥本海姆《离散时间信号处理》第三版编写，主要是为了自己学习的复习与加深。

 

 

1、在信号的数学表达式中，独立变量可以是连续的，也可以是离散的。

1）、连续时间信号时定义在一个连续时间域上，可用一个连续独立变量来表示。连续时间信号常常又称作模拟信号。

2）、离散时间信号时定义在离散时刻上的，这样独立变量便具有离散值，也就是说，离散时间信号表示成数值的序列。

3）、除了独立变量可以使连续的或离散的之外，信号幅度也可以是连续的或者离散的。

 

2、信号处理系统的分类

1）、连续时间系统是指其输入/输出都是连续时间信号的系统。

2）、离散时间系统都是其输入/输出都是离散时间信号的系统。

 

 

一、离散时间信号

1、离散时间信号在数学上表示成数的序列。

1）、一个序列x，其中序列的第n个数记作x[n]，正规地可写作

适式中n为整数。

2）、尚需序列可以通过周期采样一个模拟信号xa(t)来得到，这样一来，序列中的第n个数的数值就等于模拟信号xa(t)在时刻nT处的值，即

 

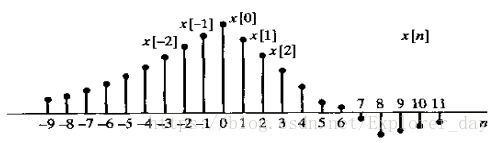
2、离散时间信号常常可以用下图表示

图中横坐标虽然画的是一条连续线，但重要的时要知道x[n]仅仅在n为整数值时才有定义，认为x[n]在n不为整数时就是零时不正确的；x[n]在n为非整数时只是无定义。

 

3、基本序列

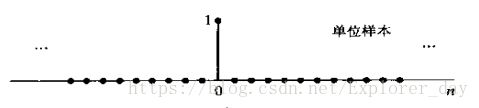
1）、单位样本序列

在离散时间时间信号与系统中单位赝本序列所引起的作用就如同单位冲激函数在连续时间信号与系统中所起的作用。为了方便起见，通常将单位样本序列称为离散时间脉冲，或者简单称为脉冲。其图示如下

单位样本序列的一个重要作用就是任何虚列都可以用一组幅度加权和延迟的单位样本序列的和来表示。

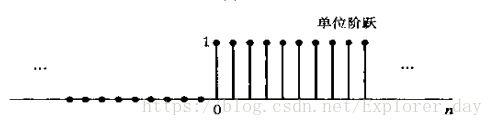
2）、单位阶跃序列

单位阶跃序列与单位样本序列的关系是

即单位阶跃序列在n时刻点的值就等于在n点及该点以前全部的单位样本值得累加和。其图示如下

利用单位样本序列表示单位阶跃的另一种形式是将单位阶跃看作是一组延迟的单位样本序列之和，如式(2.5)，即

反之，单位样本序列也可以表示成单位阶跃序列的一阶后向差分，即

3）、指数序列

I、如果A和α都是实数，则序列为实序列。如果0<α<1，A为正值，那么序列值为正，且随n增加而增加。对于-1<α<0，则序列值正负交替变化，但在幅度上仍然随n增加而减少。如果|α|>1，那么序列在幅度上就会随n增加而增加。

II、α为复数的指数序列Aαn，其实实部和虚部都是指数加权的正弦序列。具体的说，如果α=，则序列Aαn就可以表示为

若|α|>1，则该序列的包络按指数增长；若|α|<1，则包络按指数衰减。当|α|=1，该序列具有如下的形式

 

 

二、离散时间系统

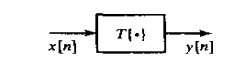
1、在数学上，一个离散时间系统可以定义一种变换或算子，它把值为x[n]的输入序列映射为值y[n]的输出序列，可以记作

并可用下图表示。

 

一）、无记忆系统

1、如果在每一个n值上的输出y[n]只决定于同一n值得输入x[n]，那么就说该系统是无记忆的。

 

二）、线性系统

1、线性系统由叠加原理来定义。如果y1[n]和y2[n]分别是输入x1[n]和x2[n]时某一系统的响应，那么当且仅当下式成立时，该系统就是线性的；

和

始终a为任意常数。

1）、上式的第一个形式称为可加性。

2）、第二个性质称为齐次性或比例性

上述两个性质结合在一起就称为叠加原理，写成

上式对任意a和b都成立。该死还可以推广到多个输入的叠加。具体地说，如果

那么一个西耐性系统的输出一定是

式中yk[n]就是系统对输入xk[n]的响应。

 

三）、时不变系统

1、时不变系统是输入序列的移位或延迟将引起输出序列的响应的移位或延迟。具体的说，假设一个系统将值为x[n]的输入序列变换成y[n]的输出序列，这个系统如果说是时不变的，则对所有n0，值为x1[n]=x[n=n0]的输入序列将产生值为y1[n]=y[n-n0]的输出序列。

 

四）、因果性

如果对每一个选取的n0，输出序列在n=n0的值仅仅取决于输入序列在n≤n0的值，则该系统就是因果。这意味着，如果x1[n]=x2[n]，n≤n0，则有y1[n]=y2[n]，n≤n0；也就是说，该系统是不可预知的。

 

五）、稳定性

1、当且仅当每一个有界的输入序列都长身一个有界的输出序列式，泽高系统在有界输入有界输出(BIBO)意义下式稳定的。如果存在某个固定的有限整数B，使下式成立；

则输入x[n]就是有界的。稳定性要求对每一个有界的输入，都存在一个固定的有界整数B，使下式成立：

 

2、特别强调的是，此定义的这些性质是系统的性质，而不是输入对某个系统的性质。这就是说，有可能找到一些输入，对这些输入浙西性质成立；但是，对某些输入存在着某个性质，并不意味着系统就有这一性质。具有这一性质的系统必须对所有输入都成立。

 

 

三、线性时不变系统

1、如果hk[n]是系统对发生在n=k的单位样本序列的响应，那么根据线性时不变系统，则有

上式结果表明，如果已知全部n对应的序列x[n]和h[n]，就有可能利用式(2.49)求出输出序列y[n]的每个样本。从这个意义上来说，一个线性时不变系统可以完全由它的单位脉冲响应h[n]来表征。上式一般称为卷积和，并用如下操作符表示；

离散时间卷积运算利用两个序列x[n]和h[n]产生第三个序列y[n]。

 

2、卷积公式解释

1）、在n=k的输入样本，由系统变换成输出系列，-∞

2）、作为公式来计算输出序列的单个值时，式(2.49)之处：y[n](也就是输出中的第n个值)是由输入系列(表示成k的函数)乘以某值为h[n-k]的序列，-∞

 

3、为了实现离散时间卷积，把两个序列x[k]和h[n-k](-∞

 

 

四、线性时不变系统的性质

1、交换律

 

2、分配律

 

3、结合律

y[n]=(x[n]*h1[n])*h2[n]=x[n]*(h1[n]*h2[n])

 

4、稳定性

一个稳定系统就是每个有界输入均产生一个有界输出的系统。当且仅当单位脉冲响应是绝对可加的，LTI系统才是稳定的，即

 

5、因果性

因果性意味着对线性时不变系统的因果性，下属条件成立：

有时也将n<0时其值为零的序列称为因果序列，它也说明因果序列可以作为因果系统的单位脉冲响应。

 

 

五、线性常系数差分方程

1、线性时不变系统中的一种重要的子系统是由这样一些系统组成的，这些系统的输入x[n]和输出y[n]满足N阶线性常系数差分方程，其形式为

 

2、如同连续时间系统的线性常系数微分方程一样，lisanongoing的线性常系数差分方程若不给出附加的限制或信息，是不能给出对出对给定输入输入情况下输出的唯一表述的。具体地说，假设对某一给定的输入xp[n]。已经一句某种方法确定了输出序列yp[n]满足线性常系数差分方程，那么在同一输入下，同一方程也能被任何一种具有如下形式的输出所满足；

始终yp[n]是当x[n]=0时的任意解，即下列方程的解；

上式称为齐次差分方程，而yh[n]称为齐次解。

 

3、如果一个系统是由一个线性常系数差分方程所表征的，并且进一步限定是线性。时不变和因果的，那么它的解就是唯一的。在这种情况下，辅助条件就玩玩说成是初始松弛条件，换言之，辅助信息就是：如果输入x[n]在n小于某个n0时为零，那么在n小于n0时输出y[n]就一定要限制到零，这样就为n≥n0利用下式

递推第求出y[n]提供了足够的初始条件。

 

4、对于一个系统，其输入和输出不是唯一的，需要一些辅助信息；

1）、对于一个给定的输入，其输出不是唯一的，需要一些辅助信息或条件。

2）、如果辅助信息是以N个顺序输出值的形式给出的，则后面的值可以将差分方程重新安排成以n的前项运算的递推关系来求出；前面的值可以将差分方程安排成以n的后向运算的递推关系来求出。

3）、系统的线性、时不变和因果性将依赖辅助条件，如果一个附加条件是使系统初始松弛的，则该系统就是线性、时不变和因果的。

以上讨论假设都假设N≥1.若果N=0，就不要递推而用差分方程来计算出，因此也不要求任何辅助条件，这就是

上式是一种军妓形式，令，其对应的单位脉冲响应为

或