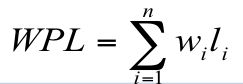哈夫曼（huffman）树和哈夫曼编码
哈夫曼（huffman）树和哈夫曼编码 — (收藏别人的博客)
学习hufffman树时看到别人写的博客，讲解细致全面，吾之楷模。收藏下，方便以后回顾，代码部分由自己实现。
原文链接：哈夫曼（huffman）树和哈夫曼编码
什么是哈夫曼树？
哈夫曼树也叫最优二叉树哈夫曼树
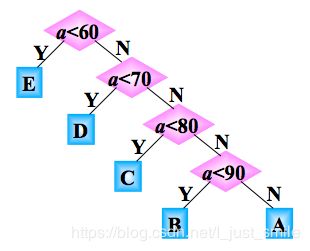
例：将学生的百分制成绩转换为五分制成绩：≥90 分: A，80～89分: B，70～79分: C，60～69分: D，＜60分: E。
if (a < 60){
b = 'E';
}
else if (a < 70) {
b = ‘D’;
}
else if (a<80) {
b = ‘C’;
}
else if (a<90){
b = ‘B’;
}
else {
b = ‘A’;
}
判别树：用于描述分类过程的二叉树。
如果每次输入量都很大，那么应该考虑程序运行的时间。
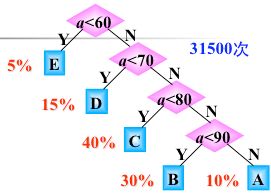
如果学生的总成绩数据有10000条，则5％的数据需 1 次比较，15％的数据需 2 次比较，40％的数据需 3 次比较，40％的数据需 4 次比较，因此 10000 个数据比较的次数为： 10000 (5％＋2×15％＋3×40％＋4×40％)＝31500次
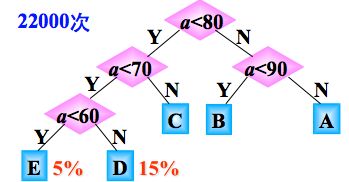
如果判别树找成另一种形状，需要的比较次数是：10000 (3×20％＋2×80％)＝22000次，显然：两种判别树的效率是不一样的。
问题：能不能找到一种效率最高的判别树呢?
那就是哈夫曼树
回忆树的基本概念和术语
路径：若树中存在一个结点序列k1,k2,…,kj，使得ki是ki+1的双亲，则称该结点序列是从k1到kj的一条路径。
路径长度：等于路径上的结点数减1。
结点的权：在许多应用中，常常将树中的结点赋予一个有意义的数，称为该结点的权。
结点的带权路径长度：是指该结点到树根之间的路径长度与该结点上权的乘积。
树的带权路径长度：树中所有叶子结点的带权路径长度之和，通常记作：
其中，n表示叶子结点的数目，wi和li分别表示叶子结点ki的权值和树根结点到叶子结点ki之间的路径长度。
赫夫曼树（哈夫曼树，huffman树）定义：
在权为w1,w2,…,wn的n个叶子结点的所有二叉树中，带权路径长度WPL最小的二叉树称为赫夫曼树或最优二叉树。
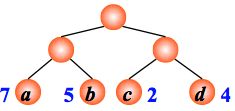
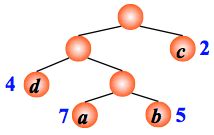
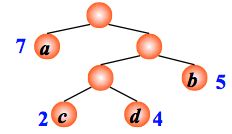
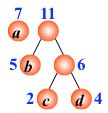
例：有4 个结点 a, b, c, d，权值分别为 7, 5, 2, 4，试构造以此 4 个结点为叶子结点的二叉树。
WPL=7´2+5´2+2´2+4´2= 36
WPL=7´3+5´3+2´1+4´2= 46
WPL=7´1+5´2+2´3+4´3= 35
WPL=7´1+5´2+2´3+4´3= 35
后两者其实就是最优二叉树（也就是哈夫曼树）。
哈夫曼树的构造(哈夫曼算法)
1.根据给定的n个权值{w1,w2,…,wn}构成二叉树集合F={T1,T2,…,Tn}，其中每棵二叉树Ti中只有一个带权为wi的根结点,其左右子树为空。
2.在F中选取两棵根结点权值最小的树作为左右子树构造一棵新的二叉树，且置新的二叉树的根结点的权值为左右子树根结点的权值之和。
3.在F中删除这两棵树，同时将新的二叉树加入F中。
4.重复2、3，直到F只含有一棵树为止。(得到哈夫曼树)
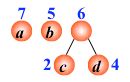
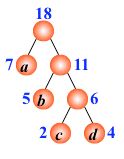
例：有4 个结点 a, b, c, d，权值分别为 7, 5, 2, 4，构造哈夫曼树。
根据给定的n个权值{w1,w2,…,wn}构成二叉树集合F={T1,T2,…,Tn},其中每棵二叉树Ti中只有一个带权为wi的根结点,其左右子树为空.
在F中选取两棵根结点权值最小的树作为左右子树构造一棵新的二叉树,且置新的二叉树的根结点的权值为左右子树根结点的权值之和.
在F中删除这两棵树,同时将新的二叉树加入F中.
重复,直到F只含有一棵树为止.(得到哈夫曼树)
关于哈夫曼树的注意点：
1、满二叉树不一定是哈夫曼树
2、哈夫曼树中权越大的叶子离根越近 （很好理解，WPL最小的二叉树）
3、具有相同带权结点的哈夫曼树不惟一
4、哈夫曼树的结点的度数为 0 或 2， 没有度为 1 的结点。
5、包含 n 个叶子结点的哈夫曼树中共有 2n – 1 个结点。（观察上图的哈夫曼树就明白了）
6、包含 n 棵树的森林要经过 n–1 次合并才能形成哈夫曼树，共产生 n–1 个新结点
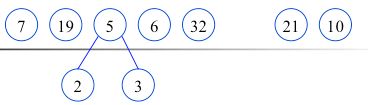
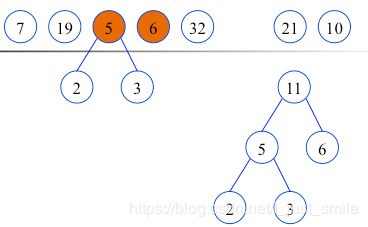
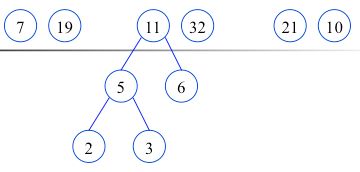
再看一个例子：如权值集合W={7,19,2,6,32,3,21,10 }构造赫夫曼树的过程。
根据给定的n个权值{w1,w2,…,wn}构成二叉树集合F={T1,T2,…,Tn},其中每棵二叉树Ti中只有一个带权为wi的根结点,其左右子树为空.
在F中选取两棵根结点权值最小的树
作为左右子树构造一棵新的二叉树，置新的二叉树的根结点的权值为左右子树根结点的权值之和
在F中删除这两棵树,同时将新的二叉树加入F中.
重复,直到F只含有一棵树为止.(得到哈夫曼树)
在F中删除这两棵树,同时将新的二叉树加入F中.
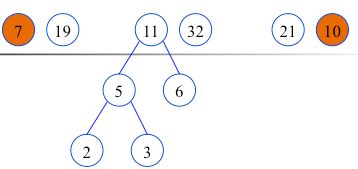
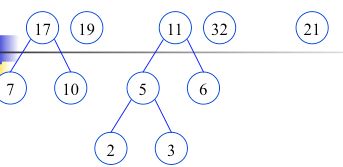
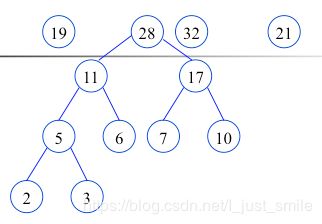
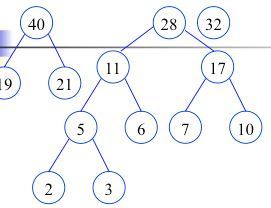
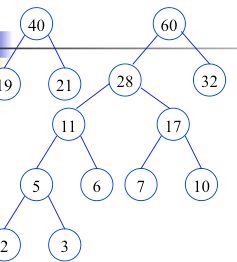
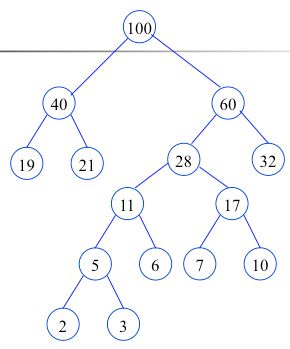
构造完毕（哈夫曼树，最优二叉树），也就是最佳判定树。由此看出，哈夫曼树不止一种形式。
哈夫曼编码
哈夫曼树的应用很广，哈夫曼编码就是其在电讯通信中的应用之一。广泛地用于数据文件压缩的十分有效的编码方法。其压缩率通常在20%～90%之间。在电讯通信业务中，通常用二进制编码来表示字母或其他字符，并用这样的编码来表示字符序列。
例：如果需传送的电文为 ‘ABACCDA’，它只用到四种字符，用两位二进制编码便可分辨。假设 A, B, C, D 的编码分别为 00, 01,10, 11，则上述电文便为 ‘00010010101100’（共 14 位），译码员按两位进行分组译码，便可恢复原来的电文。
能否使编码总长度更短呢？
实际应用中各字符的出现频度不相同，用短（长）编码表示频率大（小）的字符，使得编码序列的总长度最小，使所需总空间量最少。
数据的最小冗余编码问题
在上例中，若假设 A, B, C, D 的编码分别为 0，00，1，01，则电文 ‘ABACCDA’ 便为 ‘000011010’（共 9 位），但此编码存在多义性：可译为： ‘BBCCDA’、‘ABACCDA’、‘AAAACCACA’ 等。
译码的惟一性问题
要求任一字符的编码都不能是另一字符编码的前缀，这种编码称为前缀编码（其实是非前缀码）。 在编码过程要考虑两个问题，数据的最小冗余编码问题，译码的惟一性问题，利用最优二叉树可以很好地解决上述两个问题
用二叉树设计二进制前缀编码
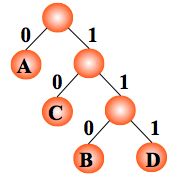
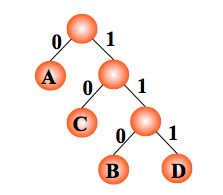
以电文中的字符作为叶子结点构造二叉树。然后将二叉树中结点引向其左孩子的分支标 ‘0’，引向其右孩子的分支标 ‘1’； 每个字符的编码即为从根到每个叶子的路径上得到的 0, 1 序列。如此得到的即为二进制前缀编码。
编码： A：0， C：10，B：110，D：111
任意一个叶子结点都不可能在其它叶子结点的路径中。
用哈夫曼树设计总长最短的二进制前缀编码
假设各个字符在电文中出现的次数（或频率）为 wi ，其编码长度为 li，电文中只有 n 种字符，则电文编码总长为：
设计电文总长最短的编码，设计哈夫曼树（以 n 种字符出现的频率作权），
由哈夫曼树得到的二进制前缀编码称为哈夫曼编码
例：如果需传送的电文为 ‘ABACCDA’，即：A, B, C, D 的频率（即权值）分别为 0.43, 0.14, 0.29, 0.14，试构造哈夫曼编码。
编码： A：0， C：10， B：110， D：111 。电文 ‘ABACCDA’ 便为 ‘0110010101110’（共 13 位）。
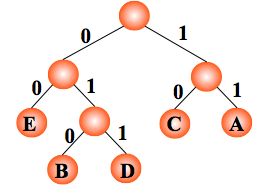
例：如果需传送的电文为 ‘ABCACCDAEAE’，即：A, B, C, D, E 的频率（即权值）分别为0.36, 0.1, 0.27, 0.1, 0.18，试构造哈夫曼编码。
编码： A：11，C：10，E：00，B：010，D：011 ，则电文 ‘ABCACCDAEAE’ 便为‘110101011101001111001100’（共 24 位，比 33 位短）。
译码
从哈夫曼树根开始，对待译码电文逐位取码。若编码是“0”，则向左走；若编码是“1”，则向右走，一旦到达叶子结点，则译出一个字符；再重新从根出发，直到电文结束。
电文为 “1101000” ，译文只能是“CAT”
哈夫曼编码算法的实现
由于哈夫曼树中没有度为1的结点，则一棵有n个叶子的哈夫曼树共有2×n-1个结点，可以用一个大小为2×n-1 的一维数组存放哈夫曼树的各个结点。 由于每个结点同时还包含其权值、字符和孩子结点的信息，所以构成的结点如下：
#include
#include 输出：
The Haffman string is:
ABCACCDAEEA
The weight is:
A: 0.363636
B: 0.0909091
C: 0.272727
D: 0.0909091
E: 0.181818
The Haffman code is:
E: 00
B: 010
D: 011
C: 10
A: 11