AT-GAN: A Generative Attack Model for Adversarial Transferring on Generative Adversarial Nets
文章目录
- 概
- 主要内容
- 符号说明
- Original Generator
- Transfer the Generator
Wang X., He K., Guo C., Weinberger K., Hopcroft H., AT-GAN: A Generative Attack Model for Adversarial Transferring on Generative Adversarial Nets. arXiv preprint, arXiv: 1904.00783, 2019.
概
用GAN生成adversarial samples, 且不需要样本(AdvGAN需要).
主要内容
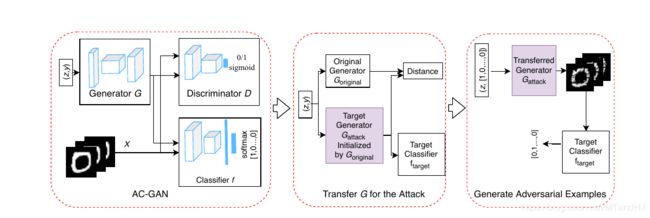
AT-GAN的训练过程主要分成俩步, 首先, 生成一个普通的条件GAN, 接着在这个条件GAN的基础上训练一个AT-GAN.
符号说明
x x x: 样本;
y y y:标签;
S y \mathcal{S}_y Sy: 标签为 y y y为图像;
z z z:随机噪声;
G ( z , y ) G(z, y) G(z,y): 生成器;
D : x → R D:x\rightarrow \mathbb{R} D:x→R: 判别器;
f ( x ) f(x) f(x): 分类器;
Original Generator
首先, 我们需要训练一个普通的条件GAN, 为此, 关于 G G G的损失函数为
L G ( z , y ) = E z ∼ p z ( z ) H ( D ( G ( z , y ) ) , 1 ) + E z ∼ p z ( z ) H ( f ( G ( z , y ) ) , y ) , (11) \tag{11} L_G(z,y)=\mathbb{E}_{z \sim p_z(z)} H(D(G(z,y)),1) + \mathbb{E}_{z \sim p_z(z)} H(f(G(z,y)),y), LG(z,y)=Ez∼pz(z)H(D(G(z,y)),1)+Ez∼pz(z)H(f(G(z,y)),y),(11)
其中 H ( a , b ) H(a,b) H(a,b)是a和b的熵(应该是指交叉熵吧, 当二分类是就是二分类熵). 显然这个损失就是希望生成器生成的图片既真实, 其标签亦为真实的标签.
关于判别器 D D D的损失则是
L D ( x , z , y ) = E x ∼ p d a t a ( x ) H ( D ( x ) , 1 ) + E z ∼ p z ( z ) H ( D ( G ( z , y ) , 0 ) . (12) \tag{12} L_D(x, z, y) = \mathbb{E}_{x \sim p_{data}(x)} H(D(x), 1)+\mathbb{E}_{z \sim p_z(z)} H(D(G(z,y),0). LD(x,z,y)=Ex∼pdata(x)H(D(x),1)+Ez∼pz(z)H(D(G(z,y),0).(12)
关于分类器的损失则是
L f ( x , y ) = E x ∼ p d a t a ( x ) H ( f ( x ) , y ) . (13) \tag{13} L_f(x,y) = \mathbb{E}_{x \sim p_{data}(x)} H(f(x),y). Lf(x,y)=Ex∼pdata(x)H(f(x),y).(13)
注: 三者分别关于 G , D , f G,D,f G,D,f最小化(虽然作者没有明讲).
Transfer the Generator
假设由上面的算法生成的生成器为 G o r i g i n a l G_{\mathrm{original}} Goriginal, 并给定我们希望攻破的分类器 f t a r g e t f_{\mathrm{target}} ftarget, 我们要构建一个新的分类器 G a t t a c k G_{\mathrm{attack}} Gattack去生成对抗样本. 显然, G a t t a c k G_{\mathrm{attack}} Gattack需要满足:
- 其生成的样本与真实样本无异, 即
∥ G o r i g i n a l ( z , y ) − G a t t a c k ( z , y ) ∥ p \| G_{\mathrm{original}}(z, y)-G_{\mathrm{attack}} (z,y)\|_p ∥Goriginal(z,y)−Gattack(z,y)∥p
足够小; - 其生成的图像能够骗过目标分类器 f t a r g e t f_{\mathrm{target}} ftarget, 最好是存在一个一一映射 g g g, 使得
f t a r g e t ( G a t t a c k ( z , y ) ) ≠ y , g ( f t a r g e t ( G a t t a c k ( z , y ) ) ) = y . f_{\mathrm{target}}(G_{\mathrm{attack}}(z, y)) \not =y, \: g(f_{\mathrm{target}}(G_{\mathrm{attack}}(z, y)))=y. ftarget(Gattack(z,y))=y,g(ftarget(Gattack(z,y)))=y.
于是作者构建了俩个损失:
L a ( z , y ) = H ( g ( f t a r g e t ( G a t t a c k ( z , y ) ) ) , y ) , (15) \tag{15} L_a(z,y)=H(g(f_{\mathrm{target}} (G_{\mathrm{attack}} (z,y))),y), La(z,y)=H(g(ftarget(Gattack(z,y))),y),(15)
L d ( z , y ) = ∥ G o r g i n a l ( z , y ) + P − G a t t a c k ( z , y ) ∥ p , (16) \tag{16} L_d (z,y) = \|G_{\mathrm{orginal}} (z,y)+P-G_{\mathrm{attack}}(z,y)\|_p, Ld(z,y)=∥Gorginal(z,y)+P−Gattack(z,y)∥p,(16)
其中 g g g是我们给定的可逆函数. 显然 L a L_a La的目的是骗过目标分类器, 而 L d L_d Ld的目的是使得生成的样本具有足够的真实性, 另外 P P P是额外加入的高斯噪声, 用于柔化距离(?).
于是训练 G a t t a c k G_{\mathrm{attack}} Gattack就是最小化下式
L ( z , y ) = α L d ( z , y ) + β L a ( z , y ) . (17) \tag{17} L(z, y)=\alpha L_{d}(z,y)+\beta L_a (z,y). L(z,y)=αLd(z,y)+βLa(z,y).(17)
注: G a t t a c k G_{\mathrm{attack}} Gattack的参数初始化为 G o r g i n a l G_{\mathrm{orginal}} Gorginal.