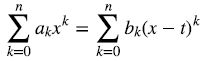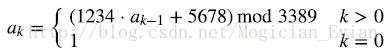NKOJ 3252 (CQOI 2015) 多项式（数学，高精度）

P3252【CQOI2015】多项式

问题描述

    在学习完二项式定理后，数学老师给出了一道题目：已知整数n,t和ak(0≤k≤n)，求bk(0≤k≤n)的表达式使得

    同学们很快算出了答案。见大家这么快就搞定了，老师便布置了一个更BT的作业：计算某个bk的具体数值！接着便在黑板上写下了n,t的数值，由于ak实在太多，不能全写在黑板上，老师只给出了一个ak的递推式，让学生自行计算  

    正在学习信息竞赛的你觉得这个作业实在不适合手工完成，便敲起了代码……

输入格式

    输入文件共三行，第一行为一个正整数n，第二行为一个非负整数t，第三行为一个非负整数m。

输出格式

    输出一行，为bm的值。

样例输入

3
2
2

样例输出

10536

提示

样例解释：
    a0=1, a1=134, a2=1584, a3=1492。
    b0=18541, b1=24374, b2=10536, b3=1492。
    1492y^3 + 1584y^2 + 134y + 1 = 1492(y-2)^3 + 10536(y-2)^2 + 24374(y-2) + 18541。

数据范围：
    对于20%的数据，t=0。
    对于另外30%的数据，n≤100000。
    对于100%的数据，0

---

根据pwj大佬提供的公式 F(x)=∑nk=0akxk=∑nk=0bk(x−t)k
抄袭pwj大佬说的在x=t处泰勒展开 F(x)=∑k=0nF(k)(t)k!(x−t)k
于是我们有 bm=F(m) (t)m!
最后再根据pwj大佬所说 F(m) (t)m!=∑n−mk=0(m+k    k)am+ktk
于是这道题就解决了。最后用高精度乱搞即可。（希望将来我能看懂上面的式子）
最后只能%%%pwj大佬。

代码

#include
#include
#include
#include
#define ll long long
using namespace std;
const ll mod=1e9;
struct Big
{
    ll S[12345],T,cur;
    void Input()
    {
        string s;cin>>s;ll i,t,l=s.length();
        for(i=0;i1)/9;S[t]=S[t]*10+s[i]-48;
            T=T*10+s[i]-48;T%=3388;
        }
        cur=(l-1)/9;while(cur>0&&S[cur]==0)cur--;
    }
    void Output()
    {
        printf("%lld",S[cur]);
        ll i,k;
        for(i=cur-1;i>=0;i--)
        {
            k=mod/10;
            while(k>S[i])putchar('0'),k/=10;
            if(k)printf("%lld",S[i]);
        }
    }
    void add(ll k)
    {
        S[0]+=k;ll i=0;
        while(S[i]>=mod)S[i+1]+=S[i]/mod,S[i++]%=mod;
        if(S[cur+1])cur++;
    }
    void ADD(const Big& o)
    {
        ll i,r=max(o.cur,cur);
        for(i=0;i<=r;i++)
        {
            S[i]+=o.S[i];
            if(S[i]>=mod)S[i+1]+=S[i]/mod,S[i]%=mod;
        }
        cur=r+5;while(cur>0&&S[cur]==0)cur--;
    }
    void Multiply(const Big& o,Big& E)
    {
        ll i,j;memset(&E,0,sizeof(E));
        for(i=0;i<=cur;i++)
        for(j=0;j<=o.cur;j++)
        {
            E.S[i+j]+=S[i]*o.S[j];
            if(E.S[i+j]>=mod)
            {
                E.S[i+j+1]+=E.S[i+j]/mod;
                E.S[i+j]%=mod;
            }
        }
        E.cur=cur+o.cur+5;
        while(E.cur>0&&E.S[E.cur]==0)E.cur--;
    }
    void Divide(ll k)
    {
        for(ll i=cur;i>0;i--)
        {
            S[i-1]+=S[i]%k*mod;S[i]/=k;
            if(S[cur]==0)cur--;
        }
        S[0]/=k;
    }
};
Big N,M,C[12],t1,t2,t3,P[12],Ans;
ll a,i,j,k,K;
int main()
{
    N.Input();P[1].Input();M.Input();
    K=N.T-M.T;if(K<0)K+=3388;
    a=1;for(i=1;i<=M.T;i++)a=(1234*a+5678)%3389;
    Ans.add(a);C[0].S[0]=1;
    for(k=1;k<=K;k++)
    {
        M.add(1);
        C[k-1].Multiply(M,C[k]);
        C[k].Divide(k);
        a=(a*1234+5678)%3389;
        P[k].Multiply(P[1],P[k+1]);
        t2.S[0]=a;
        C[k].Multiply(t2,t1);
        P[k].Multiply(t1,t3);
        Ans.ADD(t3);
    }
    Ans.Output();
}